
円周率の日
と、いうと3月14日でしょ
っていわれちゃいますが、世界では7月22日を円周率の日としている国もあるのです
それはヨーロッパなどでは日付の表し方が22/7としていて、これが約3.1428と円周率の近似値になっているからなのです
それにしても円周率は本当に興味を惹かれてやまない数ですね
円周率の値を求める計算に人生をかけたウィリアム・シャンクスは707桁まで計算しましたが、527桁までが正しくそれ以降は間違っていたとか……
かと思えばインドのラマヌジャンのように寝ている間にヒンドゥー教のナーマギリ女神が教えてくれたという数式があったり……
$${\displaystyle \frac{1}{\pi}=\frac{2\sqrt{2}}{99^2} \sum_{n=0}^\infty\frac{(4n)!(1103+26390n)}{(4^n 99^n n!)^4} }$$
$${\displaystyle \frac{4}{\pi}=\sum_{n=0}^\infty\frac{(-1)^n (4n)! (1123+21460n)}{882^{2n+1} (4^n n!)^4}}$$
2003年には東京大学の入試問題で使われました
『円周率が3.05より大きいことを示せ』
話は遡って、BC2000年頃にはバビロニアでは3.125 $${\displaystyle =3+\frac{1}{8}}$$ を円周率にしていました
また、BC1500年頃のエジプトでは3.16を円周率としていました
エジプトでは『円の面積は円の直径からその $${\displaystyle\frac{1}{9}}$$ を引いた長さを1辺とする正方形の面積に等しい』とリンド・パピルスに記されていました
現代の書き方でいうと半径を $${r}$$ とすると面積は
$${\displaystyle \left ( 2r-2r \times \frac{1}{9} \right)^2=\frac{256}{81}r^2=3.160\cdots \times r^2}$$
アルキメデス(BC287〜BC212)はそれをきちんと求めようとしました
円に接する正多角形を外側からと内側からで抑えて、その周の長さで円周の長さを挟み込もうとしたのです
そうして求めたものが今回話題の $${\displaystyle \frac{22}{7}}$$ です
また、5世紀には中国の祖沖之が円周率を $${\displaystyle \frac{355}{113}=3.141592\cdots}$$ としました
この値を『密率』と呼んでいます
一方、$${\displaystyle \frac{22}{7}}$$ のことは『約率』と呼んでいます
1590年頃にドイツではルドルフ・ファン・クーレンが円周率に興味を持ち計算を始めました
最終的に小数第35位まで求め、また本として出版もしたためドイツでは円周率のことを『ルドルフ数』ともいいます
1681年には関孝和が暦の作成にあたって円周率の近似値が必要になったため、正 131,072 $${(=4 \times 2^{15})}$$ 角形を使って小数第 16 位まで計算し、最終的に採用した近似値は「3.14159 26535 9微弱」というものでした
このように色々な人が興味からまたは必要に迫られて円周率と関わってきました
アルキメデスにチャレンジ
下の図のように正六角形から正十二角形にするだけでもかなり円周に近づきます
それでは実際にアルキメデスのように外接96角形の周の長さから円周率を求めてみましょう

外接正六角形
まずは外接正六角形から……

1辺の半分の長さを求めるには現代では1:2:√3の比を使うわけですが、アルキメデスの時代には√3はないので、唐突に153:306で三平方の定理から
265.003……を得ているようです
この3つの数が当時から知られていたのか、天啓でもたらされたのか、大きな図を描いて推測したのか分かりませんが中々に正確な数値です
これで、外接正六角形の1辺の半分の長さと円の半径の比が求まりました
外接正12角形

OB′は∠AOBの二等分線ですから
OA:OB=AB′:BB′
両辺の比の右側に左側を加えて
OA:(OA+OB)=AB′:(AB′+BB′)
OA:(OA+OB)=AB′:AB
外項を入れ替えて
AB:(OA+OB)=AB′:OA
両辺を入れ替えて
AB′:OA=AB:(OA+OB)
=153:(265+306)
=153:571
これで、外接正12角形の1辺の半分の長さと円の半径の比が求まりました
外接正24角形
続いて正24角形ですが、OB′の長さが必要になります

OB′ ²:AB′ ²=(OA²+AB′ ²):AB′ ²
=(571²+153²):153²
=349450:153²
=(591²+169):153²
OB′:AB′=591+$${\displaystyle \mathsf{\frac{1}{8}}}$$+0.017……:153
そして正12角形と同じように式を変形させていくと
OB′′は∠AOB′の二等分線ですから
OA:OB′=AB′′:B′B′′
両辺の比の右側に左側を加えて
OA:(OA+OB′)=AB′′:(AB′′+B′B′′)
OA:(OA+OB′)=AB′′:AB′
外項を入れ替えて
AB′:(OA+OB′)=AB′′:OA
両辺を入れ替えて
AB′′:OA=AB′:(OA+OB′)
=153:571+591+$${\displaystyle \mathsf{\frac{1}{8}}}$$
=153:1162+$${\displaystyle \mathsf{\frac{1}{8}}}$$
外接正48角形と外接正96角形
外接正24角形と同じように求めていきます
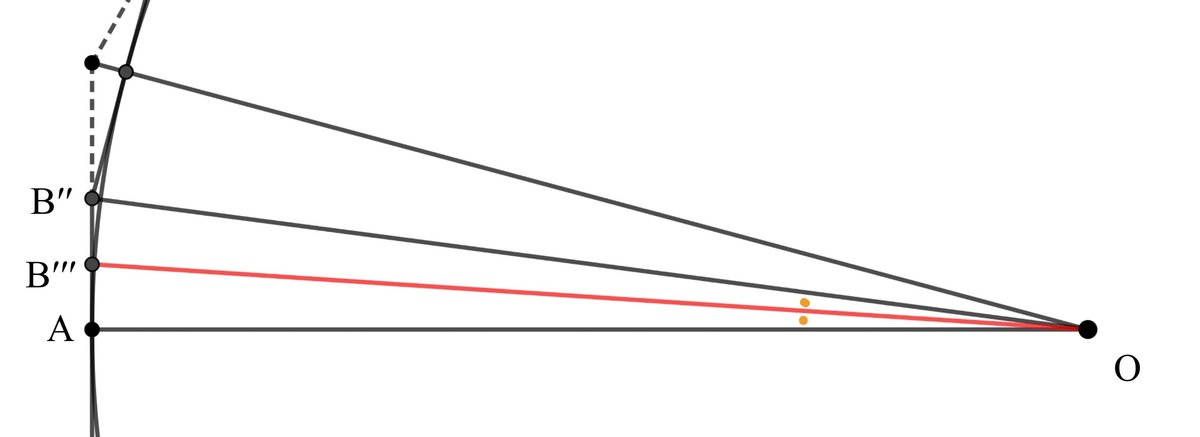
OB′′:AB′′=1172$${\displaystyle\mathsf{\frac{1}{8}}}$$+0.028……:153
となり
OB′′′は∠AOB′′の二等分線ですから
OA:OB′′=AB′′′:B′′B′′′
OA:(OA+OB′′)=AB′′′:(AB′′′+B′′B′′′)
OA:(OA+OB′′)=AB′′′:AB′′
AB′′:(OA+OB′′)=AB′′′:OA
AB′′′:OA=AB′′:(OA+OB′′)
=153:2334+$${\displaystyle \mathsf{\frac{1}{4}}}$$

正96角形も同じです
OB′′′:AB′′′=2339$${\displaystyle\mathsf{\frac{1}{4}}}$$+0.0088……:153
となり
AB′′′′:OA=AB′′′:(OA+OB′′′)
=153:4673+$${\displaystyle \mathsf{\frac{1}{2}}}$$
円周率へ
以上で正96角形の1辺の半分の長さと半径の比が分かったので円周率を求めてみたいと思います
$${円周率=\displaystyle \frac{正 \mathsf{96}角形の周の長さ}{直径}}$$ ですから
$${\displaystyle 円周率=\frac{153\times 2\times 96}{\displaystyle4673{\frac{1}{2}}\times 2}=3+\frac{1335}{9347}=3+\frac{1}{7.001\cdots}\fallingdotseq3\ \frac{1}{7}=\frac{22}{7}}$$
それにしても最初の√3の近似値といい、途中の計算の巧みさといい、あらためてアルキメデスの凄さが分かりますね
ということで7月22日は円周率の日なのです
