Lec7: 単回帰分析⑤望ましい推定量とGauss-Markov定理

皆さんこんにちは。矢野です。ここ2週間バタバタしており、更新が出来ませんでした。今日からまた更新していくので、最後までお付き合いいただければ幸いです。

さて、今日取り扱うのは、『望ましい推定量とは何か』ということです。以前、モンテカルロシミュレーションで単回帰分析を行った際、出てきた推定量の値が本当に統計的に有意であると言えるのかを検証する方法としてt検定を使用しました。今回は、もっと根本的な問題を扱います。そもそも、我々がt検定を行う際に想定する真の値とは本当に真の値なのでしょうか。また、本当の真の値はどうやったら検討がつくのでしょうか。

上の写真で挙げたように、サンプル数やどのサンプルを使うかによって、微妙に推定量の値が違うことが分かります。(一番上はβ1=1.979708(データは上から1番目～100番目の値を使用)、2番目の写真ではβ1=1.937979(101番目～200番目のデータを使用)、3番目の写真ではβ1=1.86005(201番目～300番目のデータを使用)、4番目の写真ではβ1=2.259004(1番目～10番目のデータを使用))

今回は真の値がβ1=2になるように設定したので、まあこんなものか、片づけられますが、普通は真の値はわかりません。このとき、望ましい推定量とはどのようなものであると言えるでしょうか。

ここで、『不偏性』『効率性』『有効性』という言葉がキーワードになります。

不偏性とは少なくとも期待値が真の値に一致することです。

不偏性が満足されることで、少なくとも期待値は真の値に一致するわけですから、知りたい真の値を把握することが出来るようになります。

効率性とは分散が最小であることを意味します。

いくら期待値が真の値に一致するといっても、バラツキが大きければ係数βの値を信用することが出来なくなります。分散が小さいと、より高い精度で真の値を推測することが出来るわけです。

最後に一致性について、これは推定量と真の値が一致するという意味です。

サンプル数を無限大にしたとき、推定量β^は真の値βに収束するという仮定です。当たり前ですが、真の値ではない別の値に近づくようでは回帰分析の意味がありませんので、この仮定は満たされてないと困るわけです。

これらをまとめると、

厳密には③の仮定も満たされているわけですが、今回は望ましい分布を図示するため、不偏性、効率性を満足している分布を示しています。図の赤い分布は不偏性、効率性ともに満たされています。一方で、青い分布は期待値が真の値に一致しているため不偏性は満足していますが、バラツキが大きいので効率性は満足していません。また黒い分布は期待値も真の値からかけ離れていますし、分散も大きいため不偏性、効率性ともに満足していません。

このように、不偏性、効率性、(一致性)を満足した推定量のことを最良線形不偏推定量(Best Linear Unbiased Estimator: BLUE)と言います。我々が回帰分析を行ったときは、出てきた推定量がBLUEであるかどうかを検討する必要があります。

では、推定量はどのような条件下でBLUEになるのでしょうか。ポイントは誤差項uiにあります。誤差項uiについて、OLS推定のための次のような仮定があります。(逆に言えば次の仮定を満たしていない場合はOLSとして不適切です)

上記の仮定のうち、仮定Ⅰ～Ⅳを満足している場合、推定量は不偏性を持ちます。また、仮定Ⅰ～Ⅵを満足している場合、推定量は不偏性と効率性を持ちます。仮定Ⅶに関しては、サンプル数が十分大きい場合は無視して大丈夫です。サンプル数が10個など、少ない場合にのみ気を付けなければいけない仮定です。

仮定Ⅰ～Ⅵを満足する場合、OLS推定量は最良線形不偏推定量になります。この定理のことをGauss-Markov定理と言います。

卒業論文においては、必ず仮定Ⅰ～Ⅵが満たされているか、つまり出てきた推定量が最良線形不偏推定量であるかdiscussionする必要があります。特に仮定Ⅳが満たされているかは極めて重要です。そうしたことも踏まえ、仮定Ⅰ～Ⅶの説明を最後行って今日は終わりにします。

仮定Ⅰ：線形モデルとして記述できる。

これは簡単です。モデルが足し算の形として書けていればOKです。普通は心配しなくて大丈夫です。

ただ、対数を取った時に足し算の形になってもOKです。説明変数や被説明変数の対数を取るとどうなるかについては来週説明します。

仮定Ⅱ：説明変数はバラツキが存在する

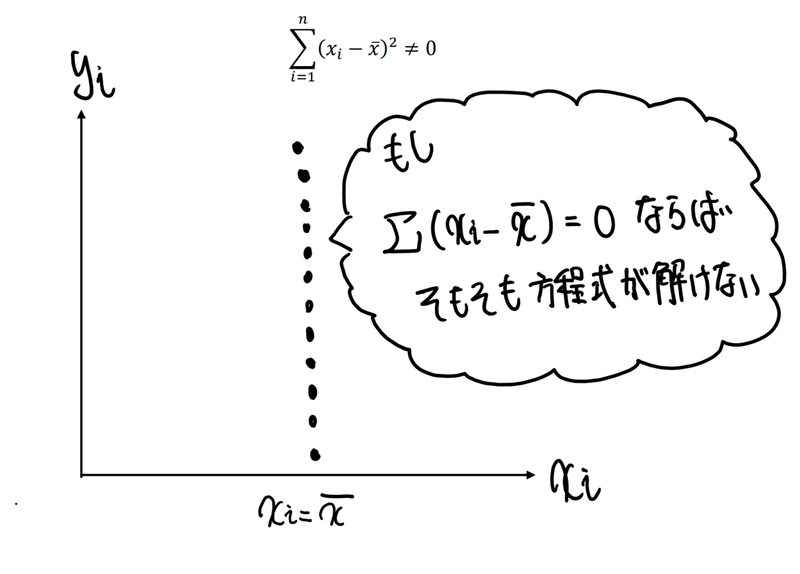
これも普通は心配ありません。そもそも、説明変数xiのデータが全て1とか同じ数字になることは基本あり得ませんからね。

仮定Ⅲ：標本(xi,yi)は独立かつ同一の分布に従う

難しい表現がなされていますが、簡単に言うと標本が無作為に抽出されていることを意味します。例えば、収入と学力との因果関係を調べたい場合、偏差値70以上の高校の生徒だけを調べるとバイアスがかかってしまいますね。ちゃんと無作為にバイアスがかからないように調べました、ということです。この仮定が満たされているかは、必ずデータを確認するようにしてください。どのような手法で得られたデータなのかを把握しておく必要があります。

仮定Ⅳ：誤差項の条件付期待値は0である。E(ui|xi)=0

仮定の意味は、説明変数xiを固定(つまり同じxiどうしを集めたもの)したときの誤差項uiの期待値が0、つまり直線上にのるということを意味します。例えば、身長と体重の関係を調べたいとき、同じ身長170cmの人の誤差項の期待値は必ず0になるということです。

この仮定は曲者です。仮定Ⅰ～Ⅲと違って、よほどのことが無い限り満たされることはありません。何故満たされないのかについては、中級(学部3年生から学部4年生向け)レベルの知識が必要なので、だいぶ後で述べることになると思いますが、これが満たされていない限り、OLS推定量は因果関係を掴んだ理想的な最良線形不偏推定量にはなりません。そして、単回帰分析では殆どこの仮定を満たすことはありません。ではどうすればいいのか、一つの方法はあと2週間後くらいから始まる重回帰分析です。説明変数の数を増やそう!ということです。いずれにせよ、卒業論文ではこの仮定については重点的に議論する必要があります。

卒業論文の段階では、この仮定は満たされていなくても構いません。ただし、何故満たされていないのか、どうすれば満たされるようになるのか、については詳細な考察を書く必要があります。自身のモデルの限界を示し、今後の課題を提供するのも研究においては重要な事です。

仮定Ⅴ：誤差項uiは互いに独立

誤差項とはあくまでどう頑張っても説明をつけることが出来ない部分のことです。誤差項同士が相関を持ったりする場合、説明がついてしまうので、それはおかしいよね、ということになります。ただし、この後扱う時系列回帰分析の場合はこの仮定が満たされていない場合が殆どなので注意が必要です。(時系列回帰分析自体は上級トピックです。修士論文ですら、よほどのことが無い限り使いません。博士論文以上で金融政策の検証を行いたい場合によく使います。私も量的緩和やマイナス金利政策について調べていますが、時系列回帰分析は使っていません。)

仮定Ⅵ：誤差項の分散は均一である

誤差項のバラツキはどこでも一定、という仮定です。これも実は満たされていないケースも多いため注意が必要です。(分散不均一：heteroscedasticity)分散が不均一かどうかを調べるには、Breusch-Pagan検定やWhite検定といった検定を使いますが、初学者向けではないためここでは割愛します。

そして、Excelで回帰分析を行う場合、分散不均一性は考慮してくれません。なので、この仮定をちゃんと考慮したい場合は統計ソフトを使う必要があります。オススメはStataです。Stataの場合

reg yy x1 ,vce(rubust)

と最後にvce(rubust)と打ち込むだけで不均一分散を考慮した頑健な(robustness)標準誤差を使った回帰分析を実行してくれます。多分これが一番簡単です。他にも一般化最小二乗法(Generalized Least Squares: GLS)を使う方法もありますが、これも上級トピック(大学院修士1年生コアコースレベル)です。

仮定Ⅶ：誤差項は正規分布に従う

この仮定はあまり気にしなくて大丈夫です。ただデータ数があまりにも少ない場合はちゃんと考慮する必要があります。まあ、そもそもデータ数が少ない場合は精度の高い推定が出来なくなるのであまり意味がないのですが....なので、この仮定は基本無視して大丈夫です。卒業論文にも明記する必要はありません。

いかがだったでしょうか。長々と書いてしましましたが、今日扱った内容は回帰分析の、計量経済学の最も重要な基本中の基本です。この内容がしっかり理解できれば、一気に中級トピックをマスターすることが出来ます。なので、Gauss-Markov定理のところは重点的に学習しておいてくださいね。

来週は単回帰分析最後になります。ダミー変数と対数変換を扱います。いずれも良く使うので、是非マスターしてください。全然難しくないので、また来週も気楽にお付き合いくださいね!

Best,

Daiki YANO