厳密な三角比の表を作ろう①「15°単位の三角比」（凪ヶ丘）

みなさんこんにちは！凪ヶ丘と申します。
私は数学や音楽、鉄道やプログラミングに興味があるので、そのことについて書いていこうと思っています。

さて、みなさんは三角比表というものを覚えていますか？
三角比(sin, cos, tanなど)の値を0°～90°まで1°単位で記した表のことですが、これらの値は無理数なので、表に載っている値は必ずしも厳密ではありません。そこで、加法定理などを用いて三角比の値を厳密に求めようと思いました。

今回はまず、簡単に求められるものから求めていこうと思います。

45°

$${sin45° = \dfrac{1}{\sqrt2}}$$
$${cos45° = \dfrac{1}{\sqrt2}}$$
$${tan45° = 1}$$

30°

$${sin30° = \dfrac{1}{2}}$$
$${cos30° = \dfrac{\sqrt3}{2}}$$
$${tan30° = \dfrac{1}{\sqrt3} = \dfrac{\sqrt3}{3}}$$

60°

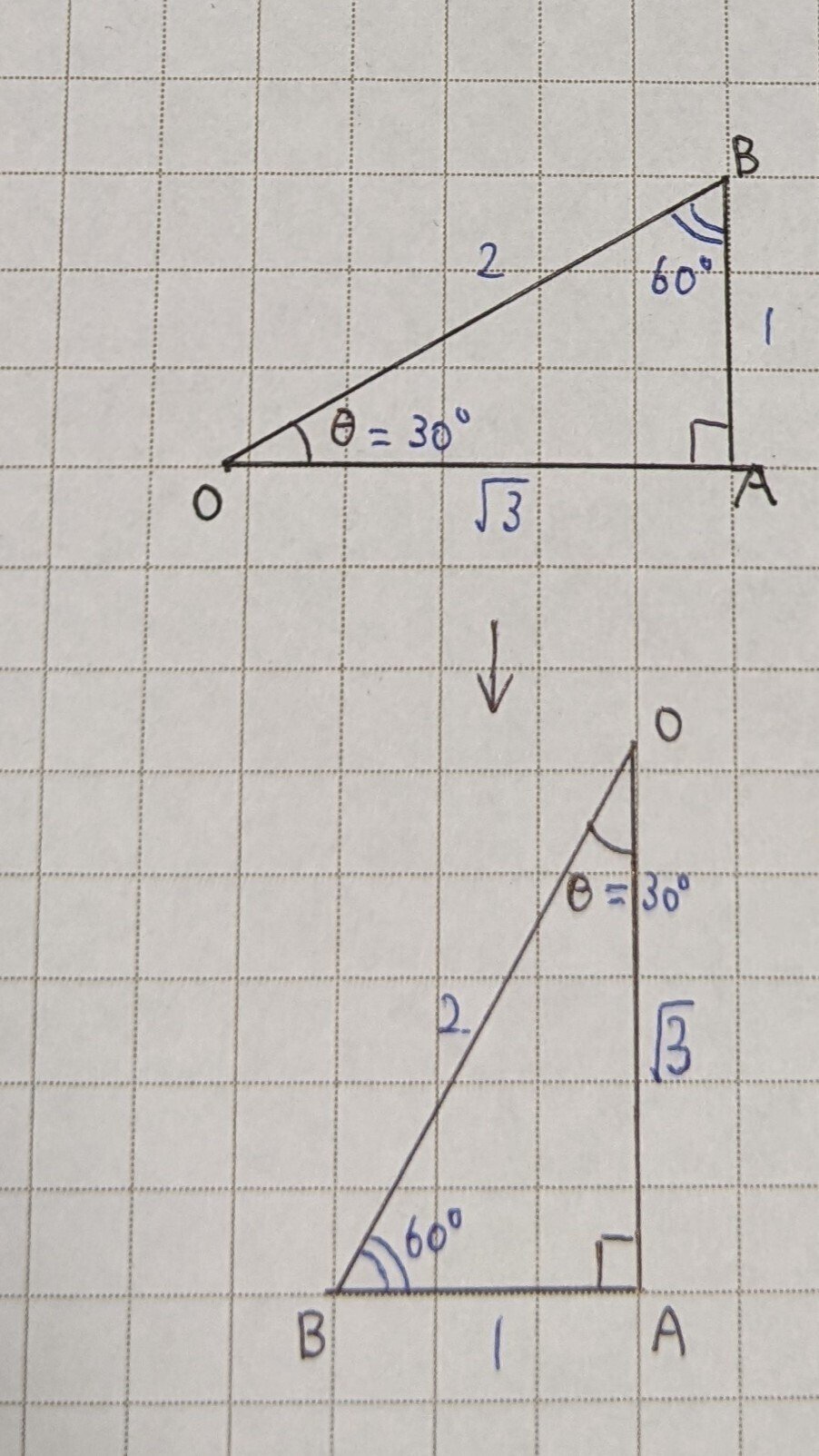
ここで三角比の変換公式
$${sin(90° - θ) = cosθ}$$
$${cos(90° - θ) = sinθ}$$
$${tan(90° - θ) = \dfrac{1}{tanθ}}$$
を使うと、
$${sin60° = cos30° = \dfrac{\sqrt3}{2}}$$
$${cos60° = sin30° = \dfrac{1}{2}}$$
$${tan60° = \dfrac{1}{tan30°} = \sqrt3}$$と表せます。

15°は少し大変ですね。このようにして表します。

15°

$${sin15° = \dfrac{1}{\sqrt6 + \sqrt2} = \dfrac{\sqrt6 - \sqrt2}{4}}$$
$${cos15° = \dfrac{2 + \sqrt3}{\sqrt6 + \sqrt2} = \dfrac{\sqrt6 + \sqrt2}{4}}$$
$${tan15° = \dfrac{1}{2 + \sqrt3} = 2 - \sqrt3}$$
また、
$${sin75° = cos15° = \dfrac{2 + \sqrt3}{\sqrt6 + \sqrt2} = \dfrac{\sqrt6 + \sqrt2}{4}}$$
$${cos75° = sin15° = \dfrac{1}{\sqrt6 + \sqrt2} = \dfrac{\sqrt6 - \sqrt2}{4}}$$
$${tan75° = \dfrac{1}{tan15°} = 2 + \sqrt3}$$
となります。

よって、現時点での表は

15°刻みの表

です。次回以降更に細かい値に取り組んでいこうと思います。
拝読してくださりありがとうございました。