輪切りスイカの原理

【問】リンゴでもスイカでも、球形の物をちょうど半分に切れば
　　　皮の部分の面積は等しくなります。
(1)　さらに半球を高さが２等分になるように切ると、
　　できた２つの物の皮の部分の面積は、さてどちらが大きいか？

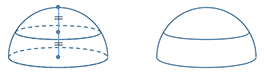
(2)　半球を高さが３等分になるように切る場合は、どうだろう？
(3)　次の定理を証明せよ。
　　スイカでもリンゴでも、球形の１つの物を
　　同じ厚さでスライスすると、皮の面積は等しくなる。

　(1) だけ、もしくは (2) だけやろうとしても、たぶん無理でしょう。結局は (3) を言わなきゃ (1) も (2) も言えないんじゃないかな。
　(3) はすなわち「ある球面を平行な２つの平面で切ってできる帯状の面積は、切る場所によらず、２平面の高さのみで決まる」ということです。ですから (1) では「２つの物の表面積は等しい」が、(2) では「３つの物の表面積は等しい」が答えです。
　直感的には中程（中心に近い部分）よりも端っこ（中心から遠い部分）の方が皮の面積が大きくなるように感じるのではないでしょうか。ところがきちんと計算してみると「中心に近い部分でも、中心から遠い部分でも、厚さが同じなら皮にあたる部分の面積は同じ」になります。またこのことから「球面を高さが n 等分になるように切ると、できた n 個の物の表面積はどれも等しくなる」こともわかります。（ただし、切って新たにできる平面の面積は除く。以下、同じ）
　この定理、「球帯の定理」と言います。別名「輪切りスイカの法則」もしくは「リンゴ皮むきの原理」とも言います。いや、ごめんなさい。いずれも、私がいま勝手に名前をつけました。ですから、そのワードでいまネット検索してもヒットしないでしょう（そのうち有名になるかもしれませんが）。

　ところで、半径 r の球の表面積が「$${S=4\pi r^2}$$」であることは中学生でも知っています。けれども「なぜそうなるか？」という説明は、中学・高校を通じて教科書のどこにも書いてありません。半径 r の球の体積が「$${V=\dfrac{4}{3}\pi r^3}$$」になることは高校の数学Ⅲでようやくきちんと説明されますが、球の表面積については最後まで説明されないのです。とは言え、微分積分を学んだ高校生なら、その考え方を理解したり面積を計算したりすることはできるでしょう。
　ここで「球全体の表面積を求める方法」をいくつか紹介しましょう。１つ目は「球をたくさんの錐体に小分けして再びかき集める」方法。この方法なら計算もほとんど要りません。２つ目は「球の体積 V(r) を半径 r で微分する」方法。機械的に微分する公式を知っていれば、即座にできます。とは言え、どちらも球の体積が「$${V=\dfrac{4}{3}\pi r^3}$$」であることを使いますので、結局のところ高校の数学Ⅲの知識を使っていることになりますが。
　ところで、その２つの方法では「球全体の表面積」を求めることはできても、残念ながら「球面を帯状に切った部分の面積」を求めることはできません。結局のところ、上の定理を証明するには「まともに積分する」するしかなさそうです。
　前置きが長くなりました。では、やってみましょう。

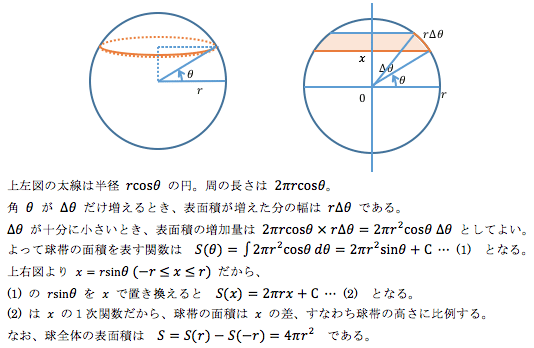
上左図の太線は半径 $${r\cos\theta}$$ の円。周の長さは $${2\pi r\cos\theta}$$。
角 $${\theta}$$ が $${\Delta \theta}$$ だけ増えるとき、表面積が増えた分の幅は $${r \Delta \theta}$$ である。
$${\Delta \theta}$$ が十分に小さいとき、
　　表面積の増加量は $${2\pi r\cos\theta \times r \Delta \theta=2\pi r^2\cos\theta \Delta \theta}$$ としてよい。
よって球帯の面積を表す関数は
　　$${S(\theta)=\int2\pi r^2\cos\theta\:d \theta=2\pi r^2\sin\theta+C}$$ … (1)　となる。
上右図より $${x=r\sin\theta\;(-r\leqq x\leqq{r})}$$ だから、
　　(1) の $${\theta}$$ を $${x}$$ で置き換えると $${S(x)=2\pi rx+C}$$ … (2)　となる。
(2) は $${x}$$ の１次関数だから、
　　球帯の面積は $${x}$$ の差、すなわち球帯の高さに比例する。
なお、球全体の表面積は $${S=S(r)-S(-r)=4\pi r^2}$$ である。

　この手の問題、わかってしまえば簡単です。でも、自分で苦労してやるからこそ、わかった後で簡単に感じるのだろうと思います。
　直感に反するように思うからこそ、証明してみる価値がある。最初は直感に反するように思えたことが、納得してしまえば「そりゃそうだ」と思える。実は私自身だいぶ苦労したのですが、私自身にとっても楽しい問題でした。

◇　　　　　　　◇　　　　　　　◇

〜 人はなぜ円周率に熱くなるのか？ 〜
▷ 円周率とは？　　　　
▷ お年玉問題　　　　　
▷ 輪切りスイカの原理