円周率とは？

　何千年も前から人は「円周率の大きさをより精度良く求める」ことに精を出してきました。そしてその動きは今も続いています。
　時を経て、円周率がいろんな場面に立ち現れることを人は知り、そして世界に潜む円周率を探し出し、炙り出すことに熱を上げるようになりました。
　3月14日に結婚して「円周率と同じように、私たちの愛は永遠に続く」と言ってるカップルがいました。私は「πラジアン＝180°、つまり半周分だ」と言ってやりました。
　すなわち円周率は、我々の歴史であり、友であり、人生の指針でもあるのです。

円周率とは？

【1】 円周率とはなんでしょうか？　定義してください。
　　　円周率とは ＿＿＿＿＿＿＿＿______________________ のことです。

【2】（Ａ）円周率は _____ から始まります。 （← １ケタの数字を入れる）
　　（Ｂ）円周率は（割り切れる ／ 割り切れない）小数です。（← 選ぶ）
　　（Ｃ）円の面積は ______________ で求められます。（← 式を入れる）

【3】上の（Ａ）,（Ｂ）,（Ｃ）から１つ選んで、
　　　なぜそう言えるのかを説明してください。

　「知ってる」ことと「分かってる」ことと「説明できる」ことはそれぞれ別物。みんなが当然知ってる円周率。使いこなしている円周率。でも、実はよくわかってない。まして他人に説明できない。そういうことを実感させるのが狙いです。

《解答例 ＆ 解説》
【1】 円周率とは「 円の直径に対する円周の長さの比」  のことです。
　　　　　　　　　　（or 直径1の円の周の長さ）

（誤答例）「円周率とは 3.14・・・のことです」
　　　　→ 「・・・」 ってナンだ？
　　　　　そんなアバウトなもんじゃ定義とは言えんでしょ。

　　　　「円周率とは 3.14159 の近似値 のことです」
　　　　→ それを言うなら逆だ。
　　　　　「3.14159 は円周率の近似値である」なら正しいが。

　　　　「円周率とは π のことです」
　　　　→「円周率を π で表す」ということなら意味は通るが、
　　　　　円周率の説明になってない。

【2】（Ａ）　円周率は　3　から始まります。
　　（Ｂ）　円周率は　割り切れない　 小数です。
　　（Ｃ）　円の面積は　半径×半径×円周率　で求められます。
　これは簡単ですね。全員正解です。生徒たちは「なにをいまさら ・・・」と思ったことでしょう。

ところが【2】を説明しようとすると、出来そうなのに出来ないんですね。
【3】 １つずつ見ていきましょう。
　まず（Ｂ）から。
白状しますが、私はなぜだか知りません。だから、当然説明できません。
これに答えるのは、高校数学のレベルを超えている。中高生には無理だ。
というわけで、（Ｂ）を選んだら、もう絶望的。（Ａ）か（Ｃ）を選ぼう。

　次に（Ｃ）。
小学校での説明は、下のようなもの。きちんとやるのは、高校「数学Ⅲ」。

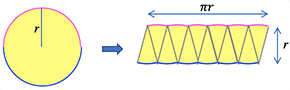
　最後に（Ａ）。
これなら中学生にも説明できます。ですから、選ぶなら、これがおススメ。
とはいえ、なかなか思いつかないでしょうけれど。では、証明いきます。

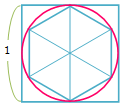
直径 1 の円の周の長さは π 。
直径 1 の円に内接する正六角形の周の長さは 3 。
直径 1 の円に外接する正方形の周の長さは 4 。
下図より、3＜π＜4 である。よって、円周率は 「3」 から始まる。//

ところで、「3」の次の数（小数第１位の数）が何か知っていますか？
あっ、ご存知ですか。それは素晴らしい。では、説明してください。（←無理でしょうけど）

東大の過去問から

【問題】 円周率が 3.05 より大きいことを証明せよ。
　　　　　　　　　　　（2003年東大入試　前期理系にて出題）

　高校範囲の余弦定理を使ったり、２重根号を外したりして解く方法がありますが、以下では中学範囲だけで解いてみます。

《解１》　半径 1 の円に内接する正８角形の１辺の長さを c とする。

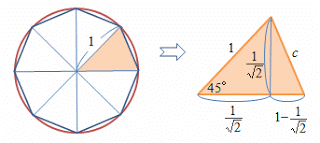
上図より　c^2 ＝ (1/√2)^2＋(1－1/√2)^2
　　　　　　　＝ 2－√2 ＞ 2－1.415 ＝ 0.585
（∵ √2＜1.415　← これが怪しいというなら、両辺を２乗せよ）
よって、c ＞ √0.585 ＞ 0.764　（← 両辺を２乗すれば確認できる）
一方、上図において「円周の長さ ＞ 正８角形の周の長さ」だから　
　　　　　　　　　　2π ＞ 8c
以上から、　π ＞ 4c ＞ 3.056 ＞ 3.05

《解２》　半径 1 の円に内接する 正12角形 の１辺の長さを c とする。

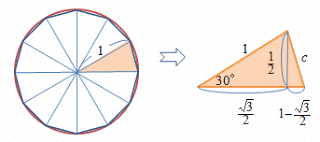
上図より　c^2 ＝ (1/2)^2＋(1－√3/2)^2
　　　　　　　＝ 2－√3 ＞ 2－1.733 ＝ 0.267
　　よって、c ＞ √0.267 ＞ 0.516
一方、上図において「円周の長さ ＞ 正12角形の周の長さ」だから　
　　　　　　　　2π ＞ 12c
　　以上から、　π ＞ 6c ＞ 3.096 ＞ 3.05

《解３》　要は多角形の辺の数が多くなれば良いわけで、必ずしも正多角形である必要はない。多分、次のやり方が、計算は最も楽。

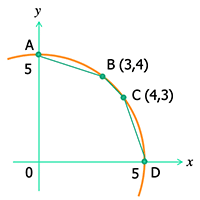
上図のように原点中心 , 半径５の円上に
　　　　A(0 , 5) , B(3 , 4) , C(4 , 3) , D(5 , 0) をとる。
　第 2 , 3 , 4 象限にも同じように点をとって、十二角形を考える。
　AB＝CD＝√10 , BC＝√2 だから 十二角形の周の長さは 4(2√10＋√2)。
　円周の長さは 10π である。
　また、√10＞3.16　,　√2＞1.41　が成り立つ。
以上から、10π＞4(2√10＋√2)＞4×(2×3.16＋1.41) ＝30.92＞30.5
　よって、π＞3.05 が成り立つ。

　ところで、この東大の【問題】「π＞3.05 を示せ」は、先に挙げた中学生向きの【問題】「円周率は __ から始まる」に比べてほんの少ししか精度が上がっていないんですね。しかも上限が不問なわけですから、「円周率は __ から始まる」の方がよほど高級だと私は思うのですが、いかがでしょうか。

◇　　　　　　◇　　　　　　◇

〜 人はなぜ円周率に熱くなるのか？ 〜
▷ 円周率とは？　　　　
▷ お年玉問題　　　　　
▷ 輪切りスイカの原理