
論理式の真偽を定義する
記号論理では「かつ(∧),または(∨),ならば(⇒),~でない(上バー)」の4つの記号を使って式(論理式)を立てます。そして、あらゆる論理式は「真(正しい)」か「偽(正しくない)」のどちらかに必ず決まります。
このことは、コンピュータの仕組みとそっくりなのです。コンピュータの内部では、究極的には「電気が流れている(on)」か「流れていない(off)」かのどちらかの状態しかありません。要するにデジタルということですが。
記号論理は、いわば「機械的な論理」です。「これこれの命令を送れば、これこれの動きをする」というように、必ず決まった動きをします。ある命令に対する動きは、いつも同じです。気まぐれに動いたりはしません。また、命令の出し方にはルール(文法)があって、厳密にそれに守らなければなりません。命令にあいまいさは許されません(コンピュータならエラーになります)。これが、ここでいう論理性です。
ところで、これが「議論の論理(普段使いの論理)」とどんな関係があるかというと、大いにあるのです。日常言語の細かいニュアンスまで表現することは出来ませんが、その骨格は(よほどグダグダの議論でなければ)やっぱり記号論理で表現できる形になっているはずからです。自分で議論を組み立てるためにも、他人の議論の骨格を身極めるためにも、記号論理に通じておくことは有益です。
ただし、記号論理で日常言語を十全に表現できるわけではありません。日常言語には、論理学ではとうてい収まりきれないほどの豊かさ・細やかさがあります。
以下、真を1で、偽を0で表しています。
論理式を真理値を定義する
○ 4つのパーツ
一例を挙げて、一般化して、論理式の真理値を定義します。
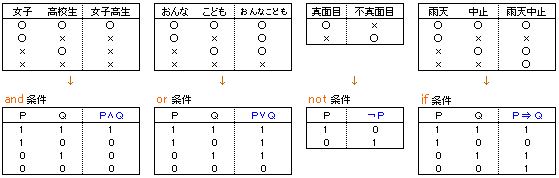
※「雨天中止」と言った場合、
「晴天(雨天でない)の場合にどうするか?」には何も触れていない。だから、晴天の場合には中止してもしなくてもウソを言ったことにはならない。よって、右端の表の3行目と4行目は真である。
○ 集合のベン図 と 電気回路
直感的にも把握しよう。
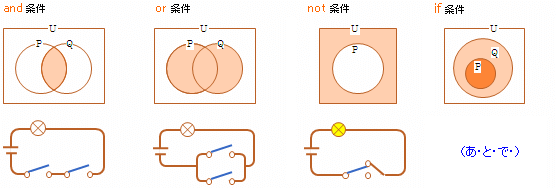
※ 電気回路の図において、
スイッチが P , Q にあたり、電球が論理式 P∧Q , P∨Q , ¬P にあたる。
P , Q がなりたつときスイッチを on に、なりたたないときスイッチを off にすると、それぞれの論理式が 真 のとき電球がつき、偽 のとき電球がつかない。(上図はすべてのスイッチが off の状態)
if 条件の具体例(ベン図でも理解しておこう)
命題 「x が 4 の倍数 ⇒ x は偶数」は 真
命題 「x が素数 ⇒ x は奇数」 は 偽
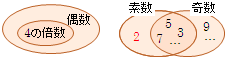
一般に、「P ⇒ Q が真」≡「P ⊂ Q」
≡:同値 P ⊂ Q:PはQの部分集合
○ 論理式の定義
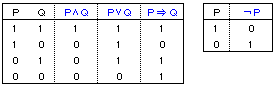
再度まとめると、下表のようになります。これが定義にあたります。この章で知っておくべきことは、これですべてです。これだけを使って、これからもっと複雑な論理式の真偽を判定していきます。そしてさらに、日常会話や議論を論理式で表して、表に1と0を書き込みながら筋が通った論か否かを判定していきます。
論理と言葉のズレ
前の節で論理式で扱う4つのパーツを定義しましたが、それと日常の感覚とではなにかとズレがあります。ここでそのズレを洗い出します。というのは、このあと学習を進める上で、そのズレがしばしば意識に現れて混乱するだろうと思うのです。ですから、早い段階でそれを知った方がむしろ理解しやすいだろうと思いますので、そうします。
ところで、なぜズレが生じるかというと、記号論理がいわば杓子定規だからです。それに対して言葉は、あいまいといえばあいまいで、豊かといえば豊かだからです。言葉には常に背景があり、ニュアンスがあり、裏があります。人は言葉から、語っていないものを読み取ったり汲み取ったりする力があります。けれども、論理はそんなものを処理できるはずがありません。
論理をうまく使いこなすためにも、論理と効用と限界を見極めるためにも、論理と言葉のズレをわきまえておくことは重要です。論理と言葉のズレは、and 条件(∧)にも or 条件(∨)にも not 条件(バー)にも if 条件(⇒)にもあります。これから1つずつ見ていきましょう。
まず、and 条件のズレから。
○ 順接と逆接を区別しない
次の2つの文章を比べてみてください。
◇ あいつはケチで、そして金持ちだ
◇ あいつは金持ちなのに、ケチだ
国語的にいうと前者は順接で、後者は逆接ということになるのでしょうが、論理式ではどちらも「金持ち、かつ、ケチ」(P∧Q)で、そこに区別はありません。

○ 順序を区別しない
次の2つの文章を比べてみてください。
◇ レストランに行って、ごはんを食べる。
◇ ごはんを食べて、レストラン行く。
昼時に誰かに「レストラン行ってごはん食べよっ」と言われれば「うん、そうしよう」と言いそうですが、「ごはん食べてレストラン行こっ」と言われたら「えっ、そんなに食えないよ」と思うんじゃないでしょうか。でも、論理的にはこの2つは同じです。どちらも「レストランに行く、かつ、ごはん食べる」ということですから。「レストランに行く」のをPと、「ごはんを食べる」をQとして、前者を「P∧Q」、後者を「Q∧P」と表したところで、両者は同値(どちらも全く同じ)です。
他に例を挙げるなら、「結婚して子供ができる」のと「子供ができて結婚する」のとでは、(倫理的には大違いでも)論理学的には全く同じだということです。人にとって時間の順序はとても大事なことですが、(意外にも?)記号論理は時間を扱えないのです。
次に、or 条件のズレ。
○ or には2種類ある?
レストランのメニューにこう書いてあったとします。「食後にコーヒーまたは紅茶がつきます」と。さて、この場面で「両方ください!」と言ったら・・・、論理学的にはそれでもいいはずなのです。「コーヒーまたは紅茶」という言い方は「コーヒーも紅茶も両方とも」の場合を含みますから。でも、普通はダメですよね。
実際、日本語で「または」というとき、「両方」を含まないことがしばしばあります。いや、「両方」を含まない方がむしろ普通かもしれません。「大きいつづらか(または)小さいつづら」と言われて、欲張りな婆さんもさすがに両方を背負って帰ろうとはしませんでした。
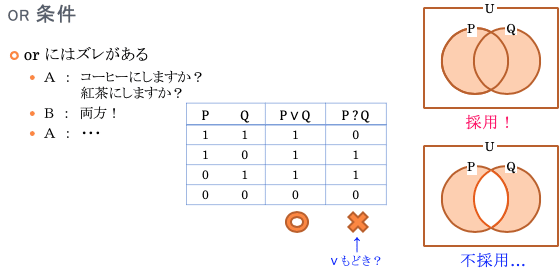
でも論理学的には、「PまたはQ」というとき、それは「PとQの少なくともどちらか一方」という意味ですから、「PとQの両方」の場合を含みます。集合の図でいうと、論理学では右上図を採用しているということです。日本語的には右下図のような意味で使われることが現実には多いのですが、こちらは不採用だということです。右下図のような意味を表にすると表の右端のようになりますが、これは「∨」ではなくて、いわば「∨もどき?」であって、論理学では使わないということです。
続いて、not 条件のズレ。
○ グレーゾーンを考えない
論理学では、世界をPとPにきれいに二分して考えます。グレーゾーンは一切考えません。
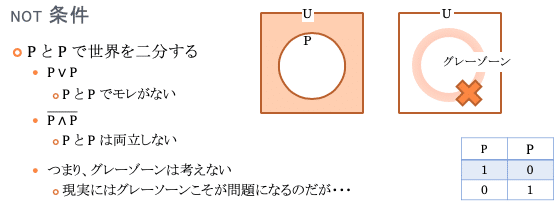
でも、現実世界で問題になるのは、まさにそのグレーゾーンなんですね。シロかクロかがはっきりしないから、考えたり議論したり裁判になったりするわけです。ところが、論理はそんなグレーゾーンを最初から想定しないということです。
否定の例として先ほど「真面目」と「不真面目」を挙げましたが、現実には「特に真面目というわけでもなく、さりとて不真面目でもない、まぁ普通」という状態がありそうですが、論理ではそれは許されないということです。
考えてみると、「グレーソーンを考えない」というのは、なかなか厳しい条件と言えるかもしれません。
最後に、if 条件のズレについて。ここが最も間違えやすいところなので、2つの視点で取り上げます。
○ 「偽 ⇒ 真」と「偽 ⇒ 偽」はどちらも真

先ほど言いました。「『雨天中止』と言った場合、『晴天(雨天でない)の場合にどうするか?』には何も触れていない。だから、晴天の場合には中止してもしなくてもウソを言ったことにはならない。よって、上表の3行目と4行目は真である」と。
同じことを違う例で説明しましょう。さて、次の命題は真でしょうか、偽でしょうか。
○ 4>5 ならば 4>3 である … ①
○ 1>5 ならば 1>3 である … ②
こう言われるとピンとこないかもしれませんね。では、次の命題はどうでしょうか。
○ x>5 ならば x>3 である … ③
これが真であることは分かると思います。さて、③が真であるというのは「x がどんな値であっても成り立つ」という意味ですね。①は x=4 の場合、②は x=1 の場合ですから、「x がどんな値であっても成り立つ」なら、①も②も成り立つ、すなわち真だとしなければ整合性が取れないわけです。もちろん、
○ 7>5 ならば 7>3 である … ④
も真です。これは③において x=7 の場合ですが、上表でいうと1行目に当たります。
では、続いて、次の命題の真偽はどうでしょうか。
○ x>3 ならば x>5 である … ⑤
これは偽ですね。なぜ偽かというと反例があるからです。x=4 の場合は成り立ちませんね。つまり x=4 が反例になるわけです。ということは、
○ 4>3 ならば 4>5 である … ⑥
は偽です。このことは上表でいうと2行目に当たります。ところで、
○ 1>3 ならば 1>5 である … ⑦
は⑤において x=1 の場合ですが、これは偽ではありません。x=1 は⑤の反例になりませんから。つまり⑦は真です。上表の4行目に当たります。
確認します。命題③は真です。だから命題①,②,④も真です。
命題⑤は偽です。だから命題⑥は偽です。でも命題⑦は真です。なお命題④と⑦はどちらも上表の4行目「偽 ならば 偽」に当たります。これは真です。
以上、真理表と整合性が取れていますね。
○ 「ならば」は因果関係を表さない
日本語で「○○ならば△△」というとき、「○○が原因となって、△△という結果が生じる」ように聞こえがちです。けれども、結論を言ってしまうと、論理の「⇒(ならば)」が示すのはあくまでも包含関係(含む、含まれるの関係)であって、論理はどうやっても因果関係(原因と結果の関係)を導いたりはしません。
言い換えると、こういうことです。論理は「どんな場合に?」という問いには答えてくれる(可能性がある)が、「なぜ?」には何も答えてくれない、ということです。
例を挙げましょう。たとえば命題「4の倍数は偶数である」(「xが4の倍数 ⇒ xは偶数である」)は真ですが、別に「4の倍数であることが原因となって、偶数という結果を生じている」わけではありません。あくまでも「4の倍数の集合は、偶数の集合の部分集合だ」と言っているにすぎません。
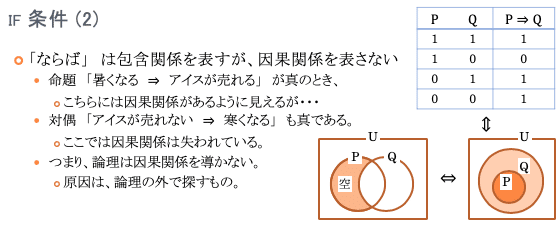
他の例を挙げましょう。「気温が上がると、アイスが売れる」(「気温が上がる ⇒ アイスが売れる」)という文を考えてみます。これは、文を読む限り、「気温上昇が原因となって、結果として売り上げがアップする」というような因果関係が感じられるでしょう。けれども、です。この文の対偶をとってみてください(「対偶」については後ほど説明します)。
命題「気温が上がる ⇒ アイスが売れる」の対偶は、「アイスが売れない ⇒ 気温が上がらない(≒下がる)」です。でも、この文からは因果関係は読み取れないでしょう。「アイスの売れ行きが原因となって、それが気温に影響を与える」なんてありえない話ですね。
ところで、元の命題とその対偶とは論理的には同値(まったく同じ)です。2つの命題が同値であるにもかかわらず、それぞれから異なった内容を解釈したのでは、論理が破たんしているというより、論理学そのものが破たんします。
ですから、先ほどの命題「気温が上がる ⇒ アイスが売れる」についても、因果関係と受け取らずに、とことん包含関係だけを読み取るべきです。右図のように「暑い日は、アイスが売れる日の一部である」と。言い換えれば、「暑くないのにアイスが売れる日もありうる」(×印、たとえば祭の日とか)ということです。
(実習1のまとめ)
ここで1時間目終了です。この時間は、まず論理式の4つのパーツを定義しました。この後の学習を通して、知っておかなければならないことはこれですべてです。
また、論理と言葉のズレについて、混乱しそうな点をいくつか挙げました。定義というのは約束事ですから無条件に受け入れるのも一つの手ですが、この後の実習でもしばしば引っかかりそうなところなので、後で無用の混乱を避けるために、先手を打ってオープンにしちゃいました。
◇ ◇ ◇
〜 デジタルな論理式 〜
▷ 論理式の真偽を定義する
▷ 論理式の真偽判定の仕方
▷ 論理式の練習問題
▷ 真理表の限界
この記事が気に入ったらサポートをしてみませんか?
