産業保健職のための疫学・統計学‐データの分析手法：重回帰分析-3重回帰分析の結果を理解する3(決定係数)

重回帰分析の結果を理解するシリーズの最後の記事です。この記事では決定係数とよばれる指標について解説していきます。

モデルはデータをどれくらい説明できるか？

ここまでの記事は、データに対して線を引くための数式（モデルと今後は呼びます）の結果、一つ一つの変数について推定値や95％信頼区間についての話をしてきました。

ここからは、モデル全体がどれくらいデータを説明できているかの指標として、決定係数と呼ばれるものについて解説していきます。決定係数はRの実行結果では、以下の青い資格で囲まれた部分に記載があります。左側が通常の決定係数で、右側が調整された決定係数です。

決定係数

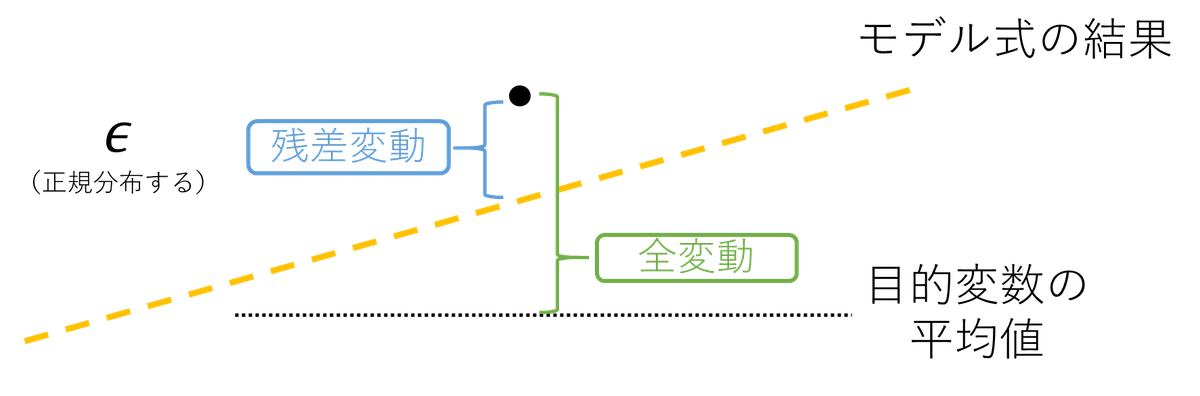
決定係数を考えるために、次のような状況を考えましょう。黄色の線が重回帰分析で推定されたモデル式だとします。そのとき、一つのデータが黒い点で表されていたとしましょう。

この時、黒い点と、モデル式の結果である黄色の点線は一致しません。データとモデル式との間には、基本的にはズレが生じるからです。重回帰分析の結果と、データとの間のズレのことを、残差変動と言ったりします。（$${\epsilon}$$、イプシロンという記号で表すことがあります。)

この残差変動、「正規分布する」ということが重回帰分析の大前提ですので、$${\epsilon}$$の分布は正規分布であるということも押さえておいてください。

それで、目的変数の平均値も同じように考えてあげます。黒い点はたくさんあるデータの一部で、たくさんあるデータの平均値が目的変数の平均値とします。

このとき、目的変数の平均値とデータとの間のズレのことを全変動といいます。

全変動の一部をモデル式が説明している部分（下図赤色）と、モデル式だけでは説明しきれない部分（下図青色、偶然の変動、残差変動）に分割して考えてあげると、

次の式のように数式を立てると、残差変動と全変動の数字を利用して、全変動の二乗のうち、モデルが説明している変動の二乗がどれくらいの割合を占めているかということを考えることができます。この、残差変動と全変動で計算できる指標が、決定係数と呼ばれるもので、この値が大きければ大きいほど、青色の残差変動の部分が少ないと考えることができ、モデルが説明している変動が大きく、データに対して良い線が引けていると考えることができます。（なお、$${\Sigma}$$記号は足し合わせるという意味の記号です。自分で計算する場合などでなければあまり気にしなくてＯＫです）

決定係数の例

データと線の関係を比較して、決定係数がどのように変わってくるかを見てみましょう。

下図の左側でデータ（青い点）が、重回帰分析で引いた線（黄色の点線）により沿ってあるということは見た目で明らかです。図の右側の黄色の点線と青い点よりも、よりデータが線に近いところにありますね？

それで、決定係数をそれぞれ計算してあげます。左側が0.759、右側が0.559で見た目通り、決定係数を利用して考えても、左側のモデルの方がデータの変動をよくとらえています。

調整済み決定係数

最初の重回帰分析結果にもどりましょう。この分析結果において、決定係数は0.4823という値になっています。これだけでも良いのかもしれませんが、実は決定係数には弱点があります。それは、重回帰分析のモデルに含む変数の数が多いほどその値が大きく出てしまうという問題です。

ちょっと実験してみます。$${y=2x+3}$$という関係性があるデータを作ってみます。回帰分析で引いた線も、データにちゃんとそっていますね？

下図の上にある表がグラフのデータです。Yの値は、Xの値に基づいて、$${y=2x+3}$$となるように計算されています（残差変動も考慮されています）。E1からE5の変数は、YやXとまったく関係なく、ランダムに0から10の数字を発生させています。そのため、このE1からE5変数を重回帰分析に入れたとしても、なんの関係もなく、意味がない行為のはずです。

このとき、$${y=\beta_0+\beta_1x}$$というモデル式で重回帰分析を行った場合に、決定係数は0.7633である一方、$${y=\beta_0+\beta_1x + \beta_2E_1\cdots + \beta_6E_5 }$$と、E1からE5までをモデル式に入れた場合の決定係数は、0.7708と、0.7633よりわずかではありますが上昇しています。

このように、意味のない変数でもモデルにたくさん変数を加えると、決定係数が高くでてしまうという弱点があります。そのため、二つのモデルのデータに対する説明度合を比べたいような場合は、決定係数ではなく、モデルの変数の数で調整した調整済み決定係数（Adjusted R-squared）という指標を用いる必要があります。
上の図の例では、YとXしか使っていないモデルでは調整済み決定係数の値は0.7609ですが、XとE1からE5まで全部使ったモデルは0.756となっており、決定係数とは逆に、変数をたくさん使うと、説明できている部分が低下しています。

まとめ

　一連の記事で重回帰分析の考え方について解説してきました。モデルを作る側になるのであれば、モデルチェックと呼ばれる、データがモデルを当てはめてよいものなのか、利用した式が本当にそれでよいのかなどを確認することを実施しなければならず、それだけで記事が5本は最低でもかけてしまうのですが、あくまで重回帰分析のイメージをつかんでもらうこのシリーズとしてはスコープから外れるため、興味がある方はぜひ成書や教科書で学んでください。

　もし、モデルを作れるようになれば、産業保健領域やヒューマンリソース領域ででてくるデータに対して、いままでより深く考察することや、単純集計では太刀打ちできない複雑な調整などができるようになるはずです。

　重回帰分析は強力なツールですが、弱点もあります。目的とする変数（Ｙ）がBMIや成績などの連続数と呼ばれるデータであればよい適応ですが、病気があるない・退職するしない・体重が減った増えたなどの「ある」
か「ない」かの2択を説明したい場合は、重回帰分析ではうまくいきません。

2択を説明する機会は医学系でよく遭遇します。そのような場合は、オッズという考え方を利用したロジスティック回帰分析という手法がよく用いられます。

次以降の記事ではロジスティック回帰分析の読み方や考え方について解説していきます。

PS 応援いただける場合は、この記事購をぜひご購入ください。