産業保健職のための疫学・統計学‐データの分析手法：重回帰分析-3重回帰分析の結果を理解する2(標準誤差、95％信頼区間)

一つ前の記事の続きです。この記事では標準誤差、95％信頼区間について解説していきます。

真の値と推定値

標準誤差について理解するために、重回帰分析で推定している推定値はどのようなものかを、点に対する線とは違う視点から見ておきましょう。

私たちが分析しようとしているデータ（下図、手元のデータ）は、世の中のすべてのデータからのほんの一部を取り出してみています。重回帰分析は、この手元のデータから色々な制限の下、分析を行い、推定値（$${\hat{\beta}}$$、ベータハット）をだしています。

この$${\hat{\beta}}$$は、もしこの世のすべてのデータを入手して同じように分析した場合に出てくる真の値($${\beta}$$、ハットはついていません)とは違います。

重回帰分析よりもう少しシンプルな状況でこの関係を見てみましょう。公平なサイコロを無限にふった場合の平均値を$${\beta}$$とします。このベータ、計算上は期待値という数値を計算することで3.5だということがわかっています。

さて、公平なサイコロを10回ふった結果の平均値を調べていましょう。お手元にサイコロがあれば、10回ふってもらってもよいですし、今回は、3,1,5,1,2,6,5,2,1,3という結果を流用いただいても大丈夫です。

この10回の結果、今回は2.9となりました。なので、真の平均値3.5とは違う値です（お手元のサイコロを振って平均値が3.5となった場合は何度か降りなおしてみてください。3.5と違う数字になるはずです。）。真の平均値とデータから得られる平均値が違うというところ、ご理解いただけましたでしょうか？

推定値の分布は？

この「サイコロを10回ふってその平均値をとる」という試みを10万回ほど繰り返してみましょう。10万回のうち最初の3回が次のような結果でした。
（10万回の手作業は無理なので、R言語でプログラムを組んでシミュレーションをしてみました）

10万回の試行の結果は次のようなヒストグラムになります。この形、どこかで見おぼえありませんか？正規分布です。推定をたくさん繰り返すと、推定値の分布は正規分布する（ことが多い）ことが知られています。（詳しくは中心極限定理というキーワードで調べてみてください。）

標準誤差

さて、私たちは真の値である$${\beta}$$を知ることができません。その代わり、手元のデータから推定した$${\hat{\beta}}$$の数値を$${\beta}$$の代わりとして議論を進めなければなりません。このとき、「$${\hat{\beta}}$$の分布の幅広さ」がどれくらいか？を表すのが標準誤差と呼ばれる指標です。

「$${\hat{\beta}}$$の分布の幅広さ」について、サイコロを10回ふった平均の分布と、サイコロを20回ふった平均の分布を見比べてみましょう。10個の平均の分布のほうが、20個の平均の分布より幅が広いことわかりますでしょうか？これは、極端な例を考えると当たり前で、10個の平均が1となる確率を考えると、$${\left(\frac{1}{6}\right)^{10}}$$と計算されますが、20個だと、$${\left(\frac{1}{6}\right)^{20}}$$です。真の平均値を中心に正規分布することには変わりませんが、極端に外れた値が出現する可能性が、データの個数が多いと低くなるため、分布の幅が狭くなります。データの数が多いと、推定した値の幅が小さくなるのは重回帰分析でも同様です。

まとめると、10回のサイコロを振った結果の平均値が2.9だったとすると、この推定した$${\hat\beta=2.9}$$という結果がどれくらい真の$${\beta}$$に近いのか？ということを表すのに、標準誤差を利用して、この標準誤差はデータそのもののばらつき、分散と、データの個数によって決まってきます。

標準誤差の具体的な計算方法は統計ソフトがやってくれますが、推定された値、$${\hat\beta}$$の分布の幅が標準誤差であるというイメージは非常に大切なため、押さえておいてください。また言い換えると、標準誤差が小さいと、推定値がより真の値に近いかもしれない、信頼できるという風に考えることもできます。

95％信頼区間

標準誤差、つまりは推定値の分布の幅の話を理解いただけたら、統計学ですごくよく出てくる95％信頼区間という指標について話を進めることができます。

まず、標準正規分布と呼ばれる、平均が0で、幅を表す分散の指標が1の正規分布を考えます。この標準正規分布、－1.96から1.96の範囲が全体の95％の面積を占めます。ということは、標準正規分布から数字をたくさん発生させると、95％の数字は-1.96から1.96の間のどこかに収まるということになります。

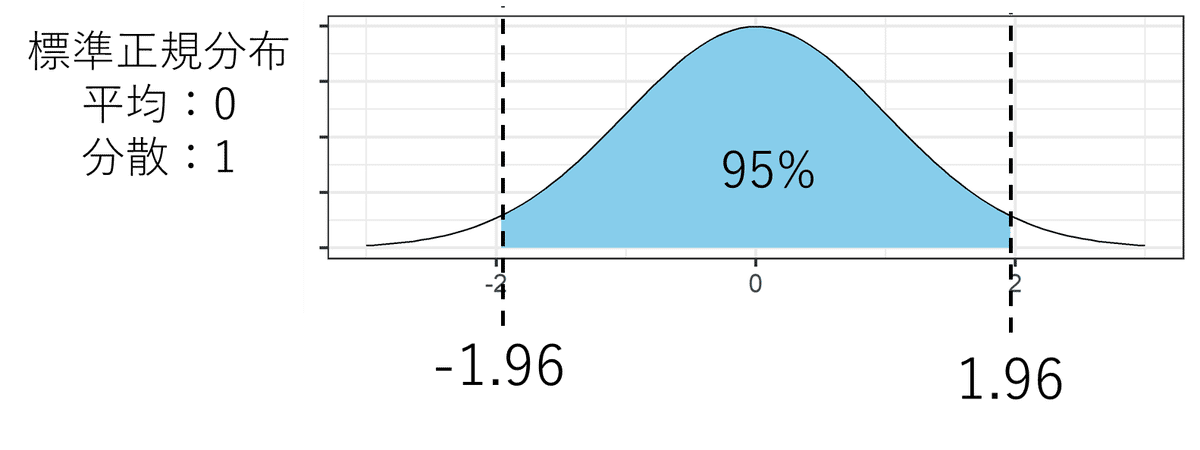
この標準正規分布、$${\hat{\beta}}$$だけ平行移動して、その幅を標準誤差だけ広げてみましょう。そうすると、－1.96から1.96の範囲は、$${\hat{\beta}-(1.96\times標準誤差)}$$から$${\hat{\beta}＋(1.96\times標準誤差)}$$の範囲になります。この範囲が95％信頼区間と呼ばれる範囲です。これ、もし推定値、$${\hat{\beta}}$$が正規分布のちょうど真ん中であった場合の、95％の数字がでてくる範囲になります。

この95％信頼区間が何を表しているのか、少し解釈がややこしいのですが、次の図を見てください。真の値、$${\beta}$$は自然界ですでに確定している値ですが、私たちはその真の値はわかりません。

入手したデータからは、推定値である$${\hat{\beta}}$$と、標準誤差から計算できる、もし推定値が正規分布のちょうど真ん中の数字であった場合の95％の数字がでてくる範囲を示しています。

もし、この推定値$${\hat{\beta}}$$と95%信頼区間をたくさん繰り返して求めたらどういうことが起きるでしょうか？$${\hat{\beta}}$$は平均を真の$${\beta}$$として正規分布する指標であるため、5%の出現する$${\hat{\beta}}$$に伴う95%信頼区間は真の$${\beta}$$を含まないはずです。つまり、95％信頼区間をたくさん発生させると、その95％個の信頼区間が真の$${\beta}$$をその信頼区間に含むはずです。逆に5％個は真の$${\beta}$$をその中に含みません。

よくある間違いが、95％信頼区間の中には95％の確率で$${\beta}$$がその範囲の中に含まれているというものです。「目の前の95%信頼区間が$${\beta}$$をその中に含んでいる確率が95%である」が正しい解釈となりますので、違いをぜひ押さえておいてください。

重回帰分析の解釈

お疲れさまでした。多分一番理解するのが難しいのが標準誤差と95％信頼区間ですが、ここまでの内容を抑えていると重回帰分析の結果を解釈することができます。

例えば、これまで例としていた重回帰分析ですが、年齢の95％信頼区間は、-0.04から0.03でゼロをまたいでいます。ということは、もしこの95％信頼区間が真の$${\beta}$$を含む95％信頼区間だった場合、$${\beta}$$はマイナスかプラスの値のどちらでも取ることができるということになります。それだと、帰無仮説、$${\beta=0}$$を否定することができず、帰無仮説が棄却できないので、有意差はないことになります。

逆に、年齢以外の変数では有意差がついており、その95％信頼区間はゼロをまたいでおらず、明らかにプラスの値かマイナスの値であることがしめされています。

いかがでしたでしょうか？次は分析全体の評価について話をすすめていきます。