
machine learning for artists
書籍執筆のための調査をしていたら「アーティストのための機械学習」というサイトを見つけたので紹介しておきます。
p5.js で伝わるだろうか、processingのデモだ。
じゃんけんの分類からStyleGANのGoogle Colabのコードなどもある。
引っ越し前のサイトにはなかなかいい読み物もある
日本語版もあるし、デモもある。
ニューラルネットワーク


MNISTのデモなんだけどこれを手で触って確認するのはいいね


ニューラルネットワークの中をのぞく
ニューラルネットワークの訓練
https://ml4a.github.io/images/figures/opt2a.gif
この素晴らしいビジュアライゼーションはAlec Radfordによるもので、今まで説明したさまざまな勾配の更新方法の特徴的な振る舞いを示しています。モーメンタム法とネステロフ加速勾配降下法(NAG)は「下り坂を転がる」速度が付きすぎて最適な経路をオーバーシュートする傾向があることに対し、標準的なSGDは適切な経路を取るものの遅すぎることに注意してください。適応的手法であるAdaGrad、AdaDelta、RMSProp(Adamもここに含まれます)はパラメータごとの柔軟性があることで、これらの問題を回避する傾向があります。

ハイパーパラメータとその評価, 過学習
過学習とは、モデルがトレーニングセットを正確に予測するように最適化され過ぎてしまい、(学習の本来の目的である)未知のデータに対応する汎用性が失われてしまっている状態のことを指します。これはモデルが、トレーニングセットに含まれるノイズまで拾って、データに完全に沿うように大きくねじ曲がってしまった場合にも起こります。
過学習とは、アルゴリズムがある種のインチキをしているのだと考えることもできます。知っているデータに対してだけ誤差が最小限になるようにして、見せ掛けだけの高得点を出せるとあなたを信じ込ませようとしているのです。これはファッションの仕組みを学ぼうとしているのに、70年代のディスコにいる人々の写真しか見たことがなくて、ベルボトム、デニムジャケット、厚底の靴が全てだと思っているようなものです。親しい友達や家族にもそんな人がいるかもしれませんね。
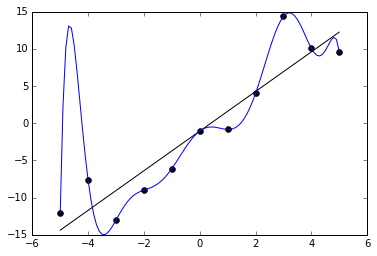
下のグラフで例を見ることができます。黒い点で示された11個のサンプルに対して適合するように、2つの関数を訓練します。1つは直線で、大まかにデータの特徴を捉えています。もう1つはとても曲がりくねった線で、全てのサンプルに完璧に一致しています。一見、後者の方が誤差が少ない(実際に0です)ので、トレーニングデータに対して良く適合しているように思えるかもしれません。しかしそれは潜在的なばらつきをうまく捉えることができておらず、未知のデータに対しては残念な性能しか出せないでしょう。
交差検証とハイパーパラメータの選択
上記の手順は過学習と戦う良い手始めになりますが、それだけでは不十分です。最適化を始める前に決めなくてはいけない重要なことがいくつかあります。どんなモデル構造を使うべきでしょうか。いくつの層と隠れたニューロンが必要でしょうか。学習率とその他のハイパーパラメータはどのように設定するべきでしょうか。単純に違う設定を試して、テストセットに対して最も良い結果を出すものを選ぶこともできます。しかし問題はこれらのハイパーパラメータを特定のテストセットだけに最適化し、任意のデータや未知のデータに適応できなくなってしまう危険があるということです。これもまた過剰な適応を行ってしまっていることになります。
これを解決するにはデータを2つではなく、トレーニングセット、検証セット、テストセットの3つに分ける方法があります。通常、データ全体の70%か80%がトレーニングセットに割かれ、残りが均等に検証セットとテストセットに分けられます。トレーニングセットを使って訓練を行い、検証セットを使って評価をして、最適なハイパーパラメータを求め、またいつ訓練を止めれば良いか(通常、検証セットに対しての精度が改善しなくなった時)を知ります。交差検証という手法がより望ましい場合もあります。トレーニングセットと検証セットは合わせていくつかの(例えば10個)等しいサイズに分けられ、それぞれの分割された部分が順番に検証セットとして用いられます。ひとつの検証セットが継続的に使われることもあります。検証の後、ずっと残して置いたテストセットを用いて最後の評価をおこないます。
訳注:交差検証ではトレーニングセットと検証セットを別々に用意するのではなく、同じデータセットを分割したものを交代で用います。例えば10個に分けたセットそれぞれに1〜10と番号を付けた場合、まず2〜10でトレーニングを行い、1で検証、次は1、3〜10でトレーニング、2で検証、というように順番に役割を交代させます。
最近では、多くの研究者が訓練プロセス自体の中でモデルの構造とハイパーパラメータを学習する方法を工夫し始めています。Google Brainの研究者はこれをAuto MLと呼んでいます。このような手法は機械学習において、未だに人間の手を必要とする退屈な部分を自動化する大きな可能性を秘めており、おそらくは誰かが問題を定義してデータセットを提供するだけで機械学習が行えるような未来を指し示しています。
正則化
正則化とは、過学習を防止するため、または好ましくない状態が起こりにくくするために、ニューラルネットワークに制約を課すことを指します。 過学習が起こるケースの1つに、重みが大きくなりすぎる場合があります。この時、上記の例で見たように関数がトレーニングセットに含まれたノイズを拾って大きくカーブしてしまうことがあります。

この正則化項は、先ほどのように大きな重みを積み重ねてひどく曲がりくねることのないようなパラメータを、勾配降下法が見つける助けになります。この他にも、L1距離または「マンハッタン距離」を用いたものなど、異なる種類の正則化項があります。これらは微妙に異なる特性を持ちますが効果としてはほぼ同じです。
ドロップアウト
ドロップアウトは2014年にNitish Srivastavaらによって導入された正則化のための巧妙なテクニックです。訓練を行う際にドロップアウトがある層に対して適用されると、接続されたニューロンのうち一定の割合(これはハイパーパラメータで一般的には20%から50%に設定されます)を無効化(ドロップアウト)します。ドロップアウトするニューロンは、訓練の間ランダムに入れ替えられます。ニューロンが必ずそこにあるとは限らなくなるため、結果としてネットワークがいくつかのニューロンに極端に依存する傾向を減らすことができます。これはネットワークがよりバランスのとれた表現を学ぶよう矯正し、過学習を防ぎます。下記はオリジナルの論文からの図解です。

過学習に対抗するため、訓練の間ドロップアウトはニューロンのいくつかをランダムに非活性化する。出典:Srivastavaらによる論文
もう1つ、正則化の変わった方法には入力に少しのノイズを加えるやり方があります。この他にも沢山の方法が提案されていますがその効果はまちまちであり、ここでは詳しく説明しません。
バックプロパゲーション
ここまで、ニューラルネットワークのパラメータを決定するための勾配降下アルゴリズムと、それをアレンジした適応的手法、またモーメンタム法などをいくつか紹介しました。どの手法を選択しても、ネットワークの重みおよびバイアスに対する損失関数の勾配を計算する必要があります。これは簡単な作業ではありません。なぜかを知るために、どうやってこれを求めるのかについて考えてみましょう。

それではどのように重みを求めるのでしょうか。事実これは、バックプロパゲーションが開発されるまでニューラルネットワークの訓練の大きな障害となっていました。誰がバックプロパゲーション(英語では「バックプロップ」と略記します)を発明したのかは論争の的になっており、多くの人々が歴史の中で別々の時期に再発明したり、様々な問題に適用される同様の概念を見つけたようです。バックプロパゲーションは、主にニューラルネットワークに関連付けられるものの、連続的微分可能な多変数関数の勾配の計算が含まれるあらゆる問題に使用することができます。そのため、その開発はニューラルネットワークの発展とはある程度並行して行われました。2014年にはJürgen Schmidhuberがバックプロパゲーションの開発の背景にある関連研究のレビューをまとめています。
バックプロパゲーションは、David Rumelhart、Geoffrey Hinton、Ronald J. Williamsによる1986年の画期的な論文の中で初めて、勾配降下法によりニューラルネットワークを最適化するタスクに用いられました。その後の研究は80年代と90年代に、最初に畳み込みネットワークに適用したYann LeCunによって行われました。ニューラルネットワークの成功は彼らとそのチームの努力によるところが大きいのです。
バックプロパゲーションの仕組みを全て説明するのは本書の範囲外です。その代わりに、この段落ではバックプロパゲーションに何ができるのかについて、基本的で大まかな考え方を説明し、技術的な説明はいくつかの参考文献に任せます。基本的な考えでは、バックプロパゲーションを用いると、単純な手法のようにパラメータごとに1つのフォワードパスを実行するのではなく、ネットワークのフォワードパスとバックワードパスで勾配のすべての要素を計算することができるようになります。これは微積分の連鎖率を利用することで可能になります。連鎖律を用いると、微分を個々の関数部分の積に分解できます。すべての接続に沿ったフォワードパスの差分を追跡、記録することで、フォワードパスの最後に損失項を求め、それを層ごとに「逆方向に誤差を伝播」して勾配を計算できます。これにより、バックワードパスはフォワードパスとほぼ同じ計算量で済むため訓練は劇的に加速し、ディープニューラルネットワークの勾配降下法は解決可能な問題になります。
バックプロパゲーションの導出方法についての詳しい技術的説明は下記のリンクを参照してください。
Further reading
How the backpropagation algorithm works by Michael Nielsen
Further reading
Hacker's guide to Neural Networks by Andrej Karpathy
Further reading
Deep Learning Basics: Neural Networks and Stochastic Gradient Descent by Alex Minnaar
Further reading
[Video] Back Propagation Derivation for Feed Forward Artificial Neural Networks by Sully Chen
Further reading
[Video] Neural network tutorial: the back-propagation algorithm (2 parts) by Ryan Harris
Further reading
Calculus on Computational Graphs: Backpropagation by Chris Olah
Further reading
A Step by Step Backpropagation Example by Matt Mazur
本章をここまでを読んだ皆さんは、本章の冒頭に登場する登山者のアナロジーの意味が分かってきたことでしょう。そうであれば、おめでとうございます。ニューラルネットワークがどのようにして訓練されるかについて理論と実践を十分に理解したので、この分野の実際の科学研究がより親しみすく思えるでしょう。何年もの間、多くの科学者は、バックプロパゲーションに対する多様かつ風変りな拡張を提案してきました。Geoffrey Hinton自身を含む他の研究者らは、機械学習はバックプロパゲーションから先へ進み、やり直さなければならないと提案しています。しかし本書の執筆時点では、バックプロパゲーションによる勾配降下法は、ニューラルネットワークやその他の多くの機械学習モデルの訓練の最も有力なパラダイムであり続け、しばらくの間はその道を歩み続けるように見えます。
続くいくつかの章では、より進んだトピックについて見ていきます。次の章では、畳み込みニューラルネットワークや特に本書の核であるアートやクリエイティブな目的への応用について紹介します
畳み込みニューラルネットワーク
福島のネオコグニトロン(1982)
ヒューベルとウィーセルの実験は、福島邦彦がニューラルネットワークで視覚野の階層的で構成的な視覚野の仕組みを模すことを試みたネオコグニトロンを考案した際に、インスピレーションとして直接言及されています。ネオコグニトロンはスライディングウィンドウを用いることで、階層になったそれぞれの層が前の層から画像の中の位置に関わらずパターンを検出することのできる構造を持った初めてのネットワークでした。

誰が翻訳したんだろ・・・これは日本人による日本語だよな・・・と思ったら稗田くんだった(東工大・世界文明センター時代の「メディアアート」の受講生)。いい仕事するじゃないか・・・!
Kenichi Yoneda
https://twitter.com/kyndinfo
カナダにでアーティストやっていたと思ったんだけど現在はドイツで活動しているのかな。
「つくる人をつくる」ってこういうところに効いてくるんだな・・・
ml4a_ さんを応援していきたい
むしろありがとうという気持ち
この記事が気に入ったらサポートをしてみませんか?
