三次元極座標(球座標)ラプラシアン表式の直観的な導出方法
イントロ
ラプラシアンは物理を学ぶ際に最も重要な作用素のひとつです。
ラプラシアンとは一体何なのか。おそらく最も初等的には、3次元直交座標 (x, y, z) を設定した上で

と定義します。
例えば (x, y, z) の関数

には

というように作用します。これを計算するのは面倒ですが、地道に計算すればできるでしょう。
ところが、物理ではしばしば系が球対称な状況を考えます。その場合、直交座標系を用いるよりも、球座標系 (r, θ, φ) を用いたほうが記述が簡単になります。
では、関数が (r, θ, φ) の関数として表されている場合、ラプラシアンはどのように作用するでしょうか?たとえば

に対してはどうでしょう?
そこで
「3次元直交座標系で定義されたラプラシアンを、球座標のことばで書き直したい」
この note では、球座標ラプラシアンの表式を簡単に思い出せる方法を紹介したいと思います。
愚直な方法
たとえば物理学科の学部の授業では、しばしば練習問題として球座標ラプラシアンの表式を計算させられます。その方法は、まず

という関係を通して、(x, y, z) の関数が (r, θ, φ) の関数になっていると考えます。たとえば上で定義した関数 u(x, y, z) も (r, θ, φ) の関数になっていて、少し計算すると実は
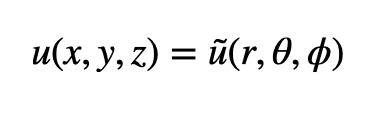
であることがわかります。両辺を入れ替えれば、逆に (r, θ, φ) の関数が (x, y, z) の関数になっていると読むこともできます。この場合、上の変数変換の式を r, θ, φ について解いて

と書いておきます。ただし、tan^{-1} の値域は場合に応じて適当に取ります。
さて、u を x で偏微分するのはいかにも面倒ですが、u~ を r や θ, あるいは φ で偏微分するのは簡単です。u を x で偏微分した結果を u~ のことばで表すとどうなるでしょうか。このようなときには、連鎖律
を用います。演算子として

という関係があり、y, z に関する偏微分についても同様です。これを用いれば、たとえば

というような計算ができます。
二階微分となると面倒ですが、計算すべきことははっきりしています。\partial / \partial x を二度作用させれば良いのですから、球座標のことばで書くと

ここで気をつけなければならないのは、ひとつめの括弧の中にある微分演算子はふたつめの括弧の中にある係数にも作用するということです。たとえばそれぞれの括弧の第一項からくる寄与には、(\partial r/ \partial x)^2 (\partial/ \partial r)^2 に加えて、橙で示した微分演算子が黄緑で示した係数に作用して与える項が含まれます。このような寄与を計算するために (r, θ, φ) を (x, y, z) で偏微分して得られる全部で9通りの係数を書き下しておきます。

ちなみにこれらを並べた行列はヤコビ行列
と呼ばれています。これらを用いて計算すると、先の二つめの括弧の第一項からくる寄与は

y, z に関する二階微分についても同様の計算を並べて書きました。これらを加えると

となって、球座標ラプラシアンの第一項を与えます。次に、先の二つめの括弧の第二項からくる寄与は、y, z に関する二階微分についても同様の計算を並べて書くと

これらの和は

これは、球座標ラプラシアンの第二項を与えます。最後に、先の二つめの括弧の第三項からくる寄与は、y, z に関する二階微分についても同様の計算を並べて書くと

これらの和は
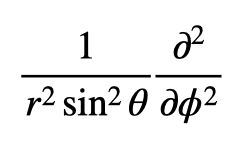
となって球座標ラプラシアンの第三項を与えます。以上の計算から、三次元ラプラシアンの球座標表示は

となります。
計算が煩雑だった割には、最後に得た式の形が綺麗に感じないでしょうか。今の導出方法では見えていない何かが背後にあると見て、各項の意味するところを明らかにしておきたいところです。
直観的な方法
ここで目指すのは、上で得た球座標ラプラシアンの表式が自然に見えるような直観的説明を与えることです。
そのために前提となる知識として、「△u は ∇u という流れの発散である」ということをはじめに説明します。簡単のために、x 方向に話を限りましょう。x 方向に流れている川があり、各点での水流が j(x) [L/s/m^2]であるとします。つまり、位置 x において、1 秒間に x 方向に流れる水量が、y および z 方向の断面積 1 m^2 あたり j(x) L であるとします。このとき、流れの導関数 j'(x) [L/s/m^3]は位置 x における 1m^3 あたりの水の湧き出しを表します。なぜなら、位置 x よりも 0.5 m 上流の流れは j(x-0.5m) ですが、0.5 m 下流では j(x+0.5m) であって、これらの差 j(x+0.5m)-j(x-0.5m) ≒ j'(x)×1m は位置 x の前後 0.5 m の範囲から湧いた水量に他ならないからです。同様に、流れの密度ベクトル (jx, jy, jz) に対して \partial jx / \partial x + \partial jy / \partial y + \partial jz / \partial z という量を計算すると、これは流れの単位体積あたり湧き出し量を表します。湧き出しのことを発散とも呼びます。
さて、ラプラシアンが関数 u(x, y, z) に作用すると

と書いてわかるように、(\partial u / \partial x, \partial u / \partial y, \partial u / \partial z) という流れの発散を与えます。
もうひとつ準備として、球座標が三次元直交座標系の空間内にどのように張られているかを思い描けなければいけません。

この図は、点 (r, θ, φ) の周りの微小体積を表しています。各変数の値を少し動かした場合に、(x, y, z) 空間内で点の移動する長さを把握しておきましょう。
以上を踏まえて、△u を計算してみます。「流れ」の密度を表すベクトルを ∇u と書くと、上の図で dr, rdθ, rsinθdφ の三方向は直交しているので、直交座標系 (x, y, z) を用いて ∇u = (\partial u / \partial x, \partial u / \partial y, \partial u / \partial z) と書けるのと同様に

ここで、各成分は dr, rdθ, rsinθdφ の各方向への流れの密度を表します。これを用いて、上図の微小体積からの湧き出し量を計算しましょう。

この図で黄色く塗った面からの流入量は 流れ密度×面積 で

と計算できます。一方で

この面からの流出量は
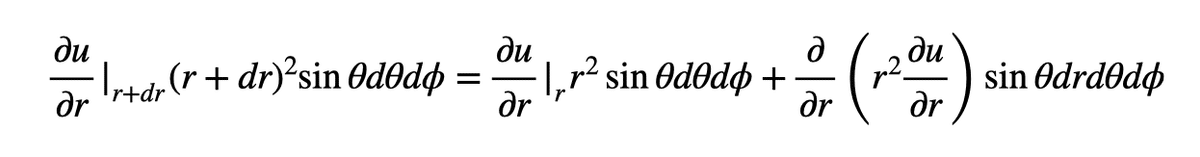
ここで、右辺第一項は上で求めた流入量です。したがって、dr 方向からの単位体積あたり湧き出しへの寄与は、右辺第二項を体積要素 r^2 sinθ drdθdφ で割って

となります。これが、球座標ラプラシアンの第一項に他なりません。他の方向についても同様にして、dθ 方向については

この面への流入量が

なので、反対側の面からの流出量との差をとって体積要素で割ると

これは球座標ラプラシアンの第二項です。dφ 方向については

この面への流入量が

ですから、反対側の面からの流出量との差をとって体積要素で割ると

これは球座標ラプラシアンの第三項です。
ということで、このような方法をとれば煩雑な計算をすることなく、直ぐに正しい表式にたどり着けます。言葉や図で述べた部分が多いため、やや厳密さに欠けるように見えるかもしれませんが、よく見比べると実は本質的に愚直な計算と同じ計算になっていることが解ります。個人的な感想としては、愚直な計算ができることが第一に重要ですが、今回述べた考え方も身につけていると、その意味が直観的に見えてなお良い、くらいでしょうか。
この記事が気に入ったらサポートをしてみませんか?
