ユニークレクタングル（とＢＵＧ）を考える

参考になる問題を紹介します。

問題１

　　問題　⇒　問題はYahoo! 知恵袋の質問から
　右側 中央と下のブロックにまたがって ユニークレクタングルがあります。それで１が決まって あとは簡単に解けますが、この解き方がとにかく眩しくて、他の解き方が全く浮かびません。

問題２

　Yahoo! 知恵袋の質問 の問題です。
　数字候補の対称性を２回使って解ける とても面白い問題です。

とても特徴的な数字候補の並びになっています。

・・・｜・・・｜・・・
・・・｜・・ａ｜・・ｄ
・・・｜・・ｂ｜・・ｃ
－－－＋－－－＋－－－
・・・｜・・・｜・・・
・・・｜・・・｜・・・
・・・｜・・・｜・・・
－－－＋－－－＋－－－
・・・｜・・・｜・・・
・・・｜・・・｜・・・
・・・｜・・・｜・・・

ａｂとｃｄはどちらも どちらか９ で、ｂとｄはどちらも ７９どちら です。
すると、
ａ９なら ｂ７ ｃ９ ｄ７ となり、ａｂｃｄが ７９の確定できない矩形 となります。
なので、ａｃは９になりません。

すると、

・・・｜・・・｜・・・
・・・｜・・・｜・・・
・・・｜・・・｜・・☆
－－－＋－－－＋－－－
・・・｜・・・｜・・・
・・・｜・・・｜・★・
・・・｜・・・｜・・・
－－－＋－－－＋－－－
・・・｜・・・｜・・・
・・・｜・・・｜・・・
・・・｜・・・｜・・・

☆★だけが数字候補が３つで、それ以外は数字候補は２つ となります。
なので、☆２でなければ★２となり、★２でなければ☆２となります（ＢＵＧ）。
☆★のどちらが２とは決められませんが、どちらか（あるいは 両方）が２なら ★の右（☆の下にもなっています）には２が入らないとわかり、ここを７と確定できます。

補足

ＢＵＧについては同じような問題が 次のページに公開されていました。
Bivalue Universal Grave Or BUG:
　Working Methodology, Types, Examples & Everything You Need to Know

r3c2=2 (if r7c2=7) or r5c3=2(if r8c3=8) → r4c2=8

問題３

　Yahoo! 知恵袋の質問 の問題です。
　ユニークレクタングルが２つ重なっている面白い問題です。

・・・｜・・・｜・・・
・・・｜・・・｜・・・
・・・｜・・・｜・・２
－－－＋－－－＋－－－
・・・｜・・・｜・・・
・・・｜・ｈ・｜・ｄ・
・・・｜ａｉ・｜・ｅ・
－－－＋－－－＋－－－
・・・｜・・・｜・・・
・・・｜ｂ・・｜・ｆ・
・・・｜ｃ・・｜・ｇ・

ａ１なら ｇ２（∵Unique Rectangles ｂｃｆｇ）で ｅ８、
ａ１でなければ ｅ８（∵Unique Rectangles ｈｉｄｅ） 、
ｅ８を確定できます。

問題４

　問題　⇒　問題はYahoo! 知恵袋の質問から
　ユニークレクタングルではありませんが、同じ考え方で解きます。
　ユニークセルとでもいうべき解き方です。

問題５

　問題　⇒　問題はYahoo! 知恵袋の質問から
　ユニークレクタングルではありませんが、同じ考え方で解きます。
　ダブル・ユニークレクタングルとでもいうべき問題です。

問題６

　問題　⇒　ナンプレ京 次の一手ナンプレ から
　ユニークレクタングルは こんな風に使うこともできる －
　なるほどのアイデアです。

問題７

　Yahoo! 知恵袋の質問 の問題です。

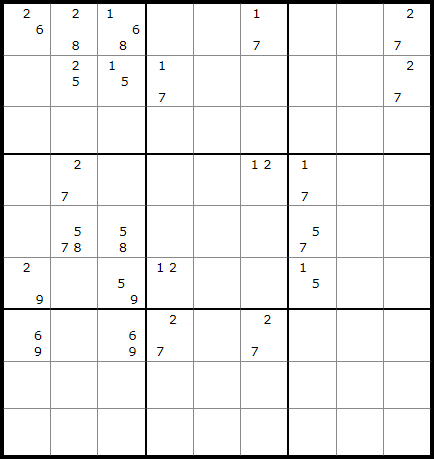
一見すると ＢＵＧの問題ですが、よく見るとＢＵＧの問題ではありません。
しかし ＢＵＧの考え方が使えます。

左側３ブロックの上段・中段以外は 候補数字がすべて２つ組です。
なので 左側上段・中段の２ブロックで答えが決まります。
そして ブロック内に候補が３つある数字のみが重要で、
ここでは 左上段の２と 左中段の５がそれに該当しますが、
左上段の２は全部２つ組になっているので除外できます。
考えるべき数字は 左中段の５です。

ーｂｃ ーーー ーーー
ーーー ーーー ーーー
ーーー ーーー ーーー

ーーー ーーー ーーー
ーｄａ ーーー ーーー
ーーー ーーー ーーー

ーーー ーーー ーーー
ーーー ーーー ーーー
ーーー ーーー ーーー

ａ８とすると、ｂ８から ｃは１６どちらか ｄは５７どちらか となって 候補数字がすべて２つ組となり、答えは一意に決まらないとわかります。
それで ａ８ではなくａ５と決まって 残りすべても決まります。