資金600万から資産1億円に到達する方法(その1、コイントスモデルに簡略化して考える)
知人から「600万円貯金があるけどどうしたら良いかな?1億円目指してFIREしたいんだけど。やっぱ個別株をタイミング見て買うのが良いかな?」、と相談を受けました。「うーん、どうかな、その方法だと資金を全部溶かす可能性が高いです」と返事をしました。最適な方法はなんでしょう?
結論から言うとインデックス投資一択です、あと本業に集中しましょう。なぜか?そこに至るための考え方をQ&A形式で解説してみます。根拠のない話をではなく数学的なモデル化、またPythonを用いたシミュレーションでも検討していきます。
下記の目次で作成しますが随時記事を継ぎ足していきます。また目次も変わって行きますので変更するかもしれません。
モデルの簡略化(コイントスの場合)
短期的なマイナスは織り込もう、資産推移は逆正弦分布する
ランダムウォーク~幾何ブラウン運動へ
タイミングをみて投資することはできない
テクニカル指標は嘘だ 市場は最適化している
株式投資で最強なのは逆説的だが株価を見ないこと
インデックスへほったらかし投資が最適解
レバレッジ投資はどうですか?
今回はモデルを簡略化してコイントスをモデルに考えます。
1.モデル簡略化してコイントス(50%の可能性で1万づつ増えるが50%の可能性で1万づつ減る場合)で考える
Q. コイントスを考えます。確率50%で当たれば1万円増える、逆に外れると1万円減るというゲームを考えます。このときに600万円からはじめて1億円に到達する可能性はどれくらいでしょうか?
上記の問いに答えるために下記のような計算をしていきます。
目標金額到達確率の導出
まず一般的な解を求めます。特定のゲームで勝つ確率 (p) と負ける確率 (q = 1 - p) を持ち、初期資金 (I) からスタートして目標金額 (T) に到達する前に破産する確率を導出するプロセスを解説します。この問題は確率過程、特にランダムウォークとマルコフ連鎖を用いてモデル化されます。
問題の定式化
勝つ確率: (p)
負ける確率: (q = 1 - p)
初期資金: (I)
目標金額: (T)
確率過程のモデル化
各試行で資金を増やすか減らすかは、独立した試行として扱われ、これをランダムウォークやマルコフ連鎖の一例として分析します。
再帰関係の定義
投資家(というよりはギャンブラー)が任意の資金額 (I) から破産する確率は、以下の再帰関係によって定義されます。
$$
P_{\text{ruin}}(I) = p \cdot P_{\text{ruin}}(I + 1) + q \cdot P_{\text{ruin}}(I - 1)
$$
ここで
$$
P_{\text{ruin}}(I + 1) と P_{\text{ruin}}(I - 1)
$$
はそれぞれ、資金が I + 1 と I - 1 の場合の破産確率を表します。
境界条件
資金が 0 の場合、投資家はすでに破産しており、破産確率は 1 です。
資金が目標金額 (T) に到達した場合、投資家は破産しておらず、破産確率は 0 です。
解の導出
再帰関係と境界条件を基に、破産確率の一般解を求めます。このプロセスには、差分方程式の解法が用いられ、結果は特性方程式の解析によって導出されます。最終的に、以下の一般解が得られます。
$$
P_{\text{reach}}(I) = \frac{1 - \left(\frac{q}{p}\right)^I}{1 - \left(\frac{q}{p}\right)^T}
$$
この式は、投資家が初期資金 (I) からスタートして目標金額 (T) に到達する確率を示しています。
$$
P_{\text{ruin}}(I) = \frac{\left(\frac{q}{p}\right)^I - \left(\frac{q}{p}\right)^T}{1 - \left(\frac{q}{p}\right)^T}
$$
この式は、投資家が初期資金 (I) からスタートして目標金額 (T) に到達する前に破産する確率を示しており、ゲームの勝敗確率比$${(\frac{q}{p}) }$$を用いて計算されます。
p=0.5、勝ち負けの可能性がいずれも50%の場合
(p = 0.5) の場合、つまり勝つ確率と負ける確率が等しい公平なゲームの場合、破産確率と目標金額に到達する確率の計算は簡略化されます。このシナリオでは、(q = 1 - p = 0.5) となり、勝つ確率と負ける確率が等しくなるため、特定の初期資金 (I) から目標金額 (T) に到達する確率は、資金の相対的位置に基づいて直接計算することができます。
(p = 0.5) の場合の解
公平なゲームの場合、投資家が目標金額 (T) に到達する確率は、初期資金 (I) と目標金額 (T) の比によって直接求めることができます。このとき、破産確率は初期資金 (I) が目標金額 (T) に対して占める割合に基づいて計算され、次のように表されます。
$$
P_{reach}(I) = \frac{I}{T}
$$
この式は、初期資金が全体の目標金額に対してどれだけの割合を占めているかを示し、その割合が直接、目標金額に到達する確率となります。
注意点
(p = 0.5) のケースでは、ゲームの性質上、勝つか負けるかの確率が等しいため、長期的には資金の増減が相殺されることが期待されます。しかし、実際の試行回数においては、ランダムな変動により短期的な資金の増減が生じることがあります。
この解析は理論的なモデルに基づいており、実際のゲームや投資戦略に適用する際には、リスク管理や資金配分の観点から慎重に検討する必要があります。
資金600万円で1億円の資産を形成できる可能性(勝率50%の場合)
(p = 0.5) の場合、つまり勝つ確率と負ける確率が等しい公平なゲームで、初期資金が 600 万円、目標金額が 1 億円(10000 万円)の場合の確率を求めます。
解
公平なゲームの場合、投資家が目標金額に到達する確率は、初期資金 (I) と目標金額 (T) の比によって直接求めることができます。
$$
P_{reach}(I) = \frac{I}{T}
$$
ここで、
(I = 600) 万円
(T = 10000) 万円
代入して計算すると、
$$
P_{reach}(600) = \frac{600}{10000} = 0.06
$$
したがって、(p = 0.5) の公平なゲームで初期資金 600 万円からスタートした場合、1 億円の資産を形成できる確率は 6% となります。逆にいうと94%は破産します。五分五分のギャンブルで1億円を形成できる可能性は高くありません。
勝率が50%より高い場合
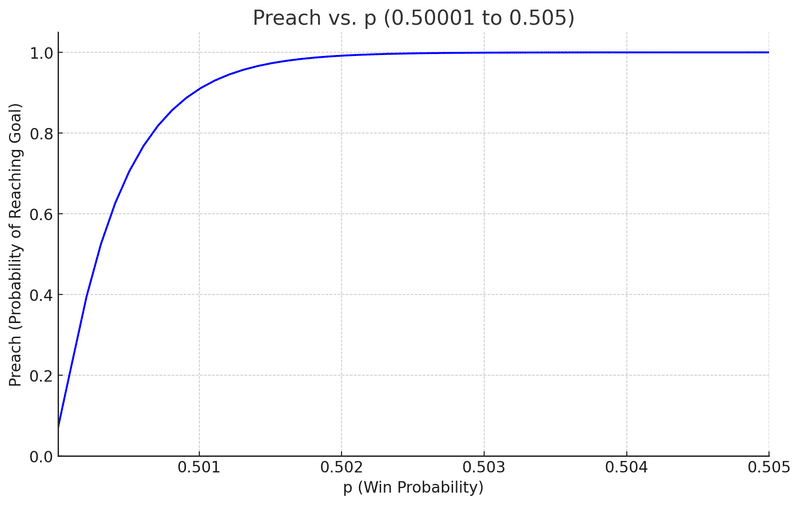
例えばp=0.51の場合はほぼ100%目標金額に到達します。p=0.501、すなわち50.1%と0.1%でも勝率が高いと90.1%となり、勝率が50.5%ですと99.9%となります。勝率が高い場合は目標金額到達率は跳ね上がります。
import numpy as np
import matplotlib.pyplot as plt
# 初期資金と目標金額を定義
I = 600 # 初期資金
T = 10000 # 目標金額
# pの値を0.50001から0.505まで0.0001刻みで生成
p_values_fine_tuned = np.arange(0.50001, 0.50501, 0.0001)
# Preachの値を格納するリスト
Preach_values_fine_tuned = []
# 各pに対してPreachを計算
for p in p_values_fine_tuned:
q = 1 - p
Preach_fine_tuned = (1 - (q/p)**I) / (1 - (q/p)**T)
Preach_values_fine_tuned.append(Preach_fine_tuned)
# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(p_values_fine_tuned, Preach_values_fine_tuned, marker='', linestyle='-', color='blue')
plt.title('Preach vs. p (0.50001 to 0.505)')
plt.xlabel('p (Win Probability)')
plt.ylabel('Preach (Probability of Reaching Goal)')
plt.grid(True)
plt.xlim(0.50001, 0.505)
plt.ylim(0, 1.05)
plt.show()
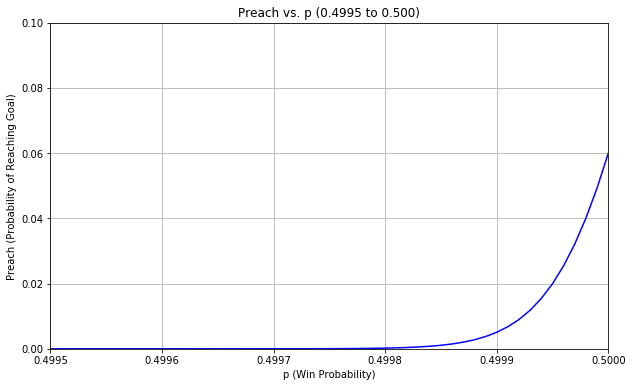
逆に勝率が50%よりわずかでも低いとどうでしょう?勝率はガクンと減ってしまいます。勝率が49.99%ですと資産1億円到達確率は0.51%、49.98%ですと0.02%とほぼ絶望的になります。
import numpy as np
import matplotlib.pyplot as plt
# 初期資金と目標金額を定義
I = 600 # 初期資金
T = 10000 # 目標金額
# pの値を0.4995から0.5まで0.00001刻みで生成
p_values_fine_tuned = np.arange(0.4995, 0.50, 0.00001)
# Preachの値を格納するリスト
Preach_values_fine_tuned = []
# 各pに対してPreachを計算
for p in p_values_fine_tuned:
q = 1 - p
Preach_fine_tuned = (1 - (q/p)**I) / (1 - (q/p)**T)
Preach_values_fine_tuned.append(Preach_fine_tuned)
# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(p_values_fine_tuned, Preach_values_fine_tuned, marker='', linestyle='-', color='blue')
plt.title('Preach vs. p (0.4995 to 0.500)')
plt.xlabel('p (Win Probability)')
plt.ylabel('Preach (Probability of Reaching Goal)')
plt.grid(True)
plt.xlim(0.4995, 0.50)
plt.ylim(0, 0.1)
plt.show()
ここから言えるメッセージは
"勝率の期待値が50%を超える投資をする、50%を下回る投資はしない"
という事になります。
勝率が50%を超えていると1億円に到達する可能性は極めて高いが時間がかかる
ここまで読まれた方は勝率が50%より高い投資(勝負)をすれば1億円に到達できるだね、簡単。でもなんでみんなできないの?と思うでしょう。時間がどれくらいかかるかを計算してみます。
目標金額 (T) に到達するまでの試行回数の期待値$${ (E[I])}$$ は、投資家が所持する金額の二乗に比例するという性質があります。具体的には、次の公式を使用して計算することができます。
公式
公平なゲームの場合、目標金額 (T) に到達するまでの試行回数の期待値 (E[I]) は以下の式で表されます。
$$
E[I] = I \times (T - I)
$$
この公式は、目標金額に到達するまでの平均試行回数を示しており、初期資金 (I) と目標金額 (T) に依存します。
計算
初期資金 (I = 600) 万円
目標金額 (T = 10000) 万円
これらの値を公式に代入して計算します。
公平なゲーム((p = 0.5))において、初期資金 (I = 600) 万円、目標金額 (T = 10000) 万円の場合、目標金額に到達するまでのゲームの試行回数の期待値は 5,640,000 回と計算されます。これは、平均して約 564万回のゲームを行う必要があることを意味します。ではp=0.6ですとどうでしょう?60%の可能性で1万円の投資額が1年で2倍になる、40%の可能性で投資額は0になる、そのような投資をイメージしてください。何年で1億円に到達しますか?
これは定式が存在しないためPythonでシミュレーションしてみます。勝率が60%(p=0.6)の場合に1億円に到達する可能性はほぼ100%ですが、約47,000回施行しないといけない、1年間で1回の投資とすると47,000年かかる計算です。p=0.51の場合はどうでしょう?この場合も1億円に到達する可能性はほぼ100%ですが、到達するまでに約470,000回施行しないといけない計算になります。
import numpy as np # numpyライブラリのインポート
# パラメータの設定
p = 0.6 # 勝つ確率
I = 600 # 初期資金
T = 10000 # 目標金額を1億円に設定
simulations = 100 # シミュレーション回数
reach_counts = 0 # 目標金額に到達した回数
trial_counts_when_reached = [] # 目標金額に到達した場合の試行回数を格納するリスト
# シミュレーションの実行
for _ in range(simulations):
funds = I # 現在の資金を初期資金で初期化
trials = 0 # 試行回数を0で初期化
while funds > 0 and funds < T:
if np.random.rand() < p:
funds += 1 # 勝った場合、資金を1単位増やす
else:
funds -= 1 # 負けた場合、資金を1単位減らす
trials += 1
if funds >= T:
reach_counts += 1
trial_counts_when_reached.append(trials)
# 目標金額に到達する確率と到達した場合の平均試行回数の計算
reach_probability = reach_counts / simulations
average_trials_when_reached = np.mean(trial_counts_when_reached) if trial_counts_when_reached else 0
print("目標金額に到達する確率:", reach_probability)
print("到達した場合の平均試行回数:", average_trials_when_reached)
時間を短縮するために1回の掛け金を増やせば良いのではないか?
例えば勝率60%の場合に1回の投資額(掛け金)を10万としてみます。その場合でも1億円に到達する可能性はほぼ100%ですが、施行回数は約4700回となります。では1回の投資額(掛け金)を100万にしてみます。そうすると資産1億円の到達可能性は91%となり、施行回数は約470回となります。投資額を思い切って300万にしてみます、そうすると資産1億の到達確率は54%、試行回数は142回となりました。
import numpy as np # numpyライブラリのインポート
# パラメータの設定
p = 0.60 # 勝つ確率
I = 600 # 初期資金
T = 10000 # 目標金額を1億円に設定
simulations = 100 # シミュレーション回数
reach_counts = 0 # 目標金額に到達した回数
trial_counts_when_reached = [] # 目標金額に到達した場合の試行回数を格納するリスト
# シミュレーションの実行
for _ in range(simulations):
funds = I # 現在の資金を初期資金で初期化
trials = 0 # 試行回数を0で初期化
while funds > 0 and funds < T:
if np.random.rand() < p:
funds += 300 # 勝った場合、資金を300単位増やす
else:
funds -= 300 # 負けた場合、資金を300単位減らす
trials += 1
if funds >= T:
reach_counts += 1
trial_counts_when_reached.append(trials)
# 目標金額に到達する確率と到達した場合の平均試行回数の計算
reach_probability = reach_counts / simulations
average_trials_when_reached = np.mean(trial_counts_when_reached) if trial_counts_when_reached else 0
print("目標金額に到達する確率:", reach_probability)
print("到達した場合の平均試行回数:", average_trials_when_reached)掛け金を変えた場合は上記の例ではPythonのシミュレーションで出していますが実は一般解が求まります。
掛け金を (n) 倍にすることで初期資金 (I) と目標金額 (T) をそれぞれ (n) で割った新しい初期資金 (I' = I/n) と新しい目標金額 (T' = T/n)と考えることができます。
目標金額に到達する確率の式は次のように更新されます。
既存の式:
$$
P_{\text{reach}}(I) = \frac{1 - \left(\frac{q}{p}\right)^I}{1 - \left(\frac{q}{p}\right)^T}
$$
新しい初期資金 (I') と新しい目標金額 (T') を用いた場合の更新された式は、次のようになります。
$$
P_{\text{reach}}(I') = \frac{1 - \left(\frac{q}{p}\right)^{I'}}{1 - \left(\frac{q}{p}\right)^{T'}}
$$
ここで、(I' = I/n) と (T' = T/n) です。したがって、具体的には次の式に置き換えられます。
$$
P_{\text{reach}}\left(\frac{I}{n}\right) = \frac{1 - \left(\frac{q}{p}\right)^{\frac{I}{n}}}{1 - \left(\frac{q}{p}\right)^{\frac{T}{n}}}
$$
この式は、掛け金を (n) 倍に調整した場合の新しい条件下での目標金額に到達する確率を示しており、掛け金の調整が初期資金と目標金額のスケールにどのように影響するかを考慮しています。勝率が50%より高い場合は、1回の掛け金を増やすと勝率は低下します。
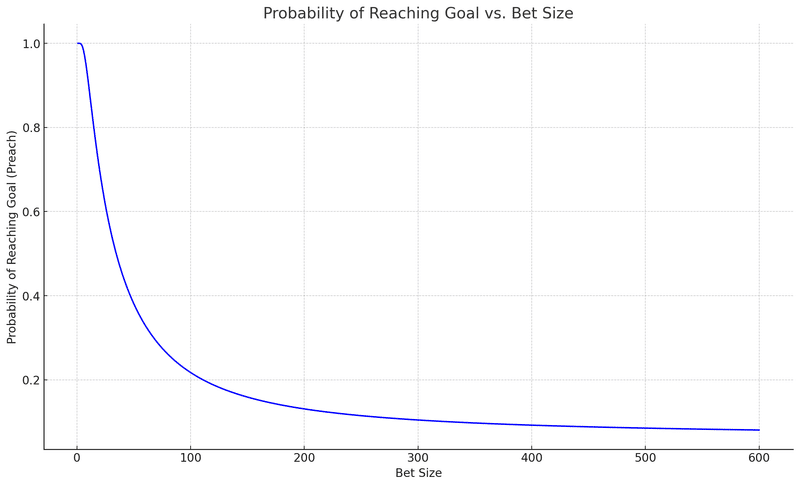
勝率が50.1%の場合に投資額を1~600まで変化させると勝率は下図のように下がっていきます。
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
p = 0.51 # 勝つ確率
q = 1 - p # 負ける確率
I = 600 # 初期資金
T = 10000 # 目標金額
bet_range = range(1, 601) # 掛け金の範囲 (1~600)
# Preachの計算
Preach_values = [(1 - (q/p)**(I/bet)) / (1 - (q/p)**(T/bet)) for bet in bet_range]
# グラフの描画
plt.figure(figsize=(14, 8))
plt.plot(bet_range, Preach_values, marker='', linestyle='-', color='blue')
plt.title('Probability of Reaching Goal vs. Bet Size')
plt.xlabel('Bet Size')
plt.ylabel('Probability of Reaching Goal (Preach)')
plt.grid(True)
plt.show()ここから言えるメッセージは
"勝率が高い場合でも1回の投資額を増やすと破産する可能性が高まる”
という事になります。絶対にこれはいける、という投資案件があったとします、それは何%の勝率ですか?、本当にあなたしか知らない情報をもとにした投資ですか?、投資額は適切ですか?というメッセージになります。
疲れたのでまた元気があるときに続きを書きます。
この記事が気に入ったらサポートをしてみませんか?
