
Statistical Mechanics: Theory and Molecular Simulation Chapter 4 - The canonical ensemble
Statistical Mechanics: Theory and Molecular SimulationはMark Tuckermanによって著された分子シミュレーションに関連した熱・統計物理学,及び量子力学の参考書になります。
現時点では(恐らく)和訳がないこともあり,日本での知名度はあまりないような気がしますが,被引用数が1300を超えていることを考えると海外では高く認知されている参考書みたいです。
本記事では,Chapter 4(The canonical ensemble)の章末問題の和訳とその解答例を紹介します。解答例に間違いが見受けられた場合はお知らせいただけると助かります。
Problem 4.1
式(4.8.15)のNose–Poincareハミルトニアンのミクロカノニカル分配関数が物理的なハミルトニアン$${\mathcal{H}(\mathbf{r},\mathbf{p})}$$のカノニカル分配関数と等価であることを示せ。式(4.8.15)に含まれるパラメータ$${g}$$の値をどう選ぶべきか?
$$
\begin{align*}
\tilde{\mathcal{H}}_{\rm N}&=\left(\mathcal{H}_{\rm N}(\mathbf{r},s,\mathbf{p},p_s)-\mathcal{H}_{\rm N}^{(0)}\right)s\\
\mathcal{H}_{\rm N}(\mathbf{r},s,\mathbf{p},p_s)&=\sum_{i=1}^N\frac{\mathbf{
p}_i^2}{2m_is^2}+U(\mathbf{r}_1,\cdots,\mathbf{r}_N)+\frac{p_s^2}{2Q}+gk_{\rm B}T\ln s
\end{align*}\tag{4.8.15}
$$
Nose–Poincareハミルトニアンのミクロカノニカル分配関数を$${\Omega}$$とすると
$$
\begin{align*}
\Omega&\propto\int{\rm d}^N\mathbf{r}\int{\rm d}^N\mathbf{p}\int{\rm d}s\int{\rm d}p_s\delta\left(\tilde{\mathcal{H}}_{\rm N}-0\right)\\
&=\int{\rm d}^N\mathbf{r}\int{\rm d}^N\mathbf{p}\int{\rm d}s\int{\rm d}p_s\delta\left(\left\{\sum_{i=1}^N\frac{\mathbf{
p}_i^2}{2m_is^2}+U(\mathbf{r}_1,\cdots,\mathbf{r}_N)+\frac{p_s^2}{2Q}+gk_{\rm B}T\ln s-\mathcal{H}_{\rm N}^{(0)}\right\}s\right)\\
&=\int{\rm d}^N\mathbf{r}\int{\rm d}^N\mathbf{p}_s\int{\rm d}s\int{\rm d}p_ss^{dN}\delta\left(\left\{\sum_{i=1}^N\frac{\mathbf{
p}_i^2}{2m_i}+U(\mathbf{r}_1,\cdots,\mathbf{r}_N)+\frac{p_s^2}{2Q}+gk_{\rm B}T\ln s-\mathcal{H}_{\rm N}^{(0)}\right\}s\right)\\
&=\int{\rm d}^N\mathbf{r}\int{\rm d}^N\mathbf{p}\int{\rm d}s\int{\rm d}p_ss^{dN}\delta\left(\left\{\mathcal{H}(\mathbf{r},\mathbf{p})+\frac{p_s^2}{2Q}+gk_{\rm B}T\ln s-\mathcal{H}_{\rm N}^{(0)}\right\}s\right)\\
&=\int{\rm d}^N\mathbf{r}\int{\rm d}^N\mathbf{p}\int{\rm d}s\int{\rm d}p_ss^{dN}\frac{\delta\left(s-\exp\left(-\frac{\mathcal{H}(\mathbf{r},\mathbf{p})+\frac{p_s^2}{2Q}-\mathcal{H}_{\rm N}^{(0)}}{gk_{\rm B}T}\right)\right)}{gk_{\rm B}T}\\
&=\frac{1}{gk_{\rm B}T}\int{\rm d}^N\mathbf{r}\int{\rm d}^N\mathbf{p}\int{\rm d}p_s\exp\left(-\frac{dN}{g}\frac{\mathcal{H}(\mathbf{r},\mathbf{p})+\frac{p_s^2}{2Q}-\mathcal{H}_{\rm N}^{(0)}}{k_{\rm B}T}\right)\\
&=\frac{1}{gk_{\rm B}T}\exp\left(\frac{dN}{g}\frac{\mathcal{H}_{\rm N}^{(0)}}{k_{\rm B}T}\right)\left\{\int{\rm d}p_s\exp\left(-\frac{dN}{g}\frac{\frac{p_s^2}{2Q}}{k_{\rm B}T}\right)\right\}\int{\rm d}^N\mathbf{r}\int{\rm d}^N\mathbf{p}\exp\left(-\frac{dN}{g}\frac{\mathcal{H}(\mathbf{r},\mathbf{p})}{k_{\rm B}T}\right)
\end{align*}
$$
と式変形できる。
$${g=dN}$$に選ぶことにより,
$$
\begin{align*}
\Omega&\propto\int{\rm d}^N\mathbf{r}\int{\rm d}^N\mathbf{p}\exp\left(-\frac{\mathcal{H}(\mathbf{r},\mathbf{p})}{k_{\rm B}T}\right)
\end{align*}
$$
となり,これは$${\mathcal{H}(\mathbf{r},\mathbf{p})}$$のカノニカル分配関数と等価であることを意味する。
Problem 4.2
運動量$${p}$$と座標$${q}$$の一次元系に熱浴の役割を果たす変数を組み合わせた拡張系が以下の運動方程式に従うとする。
$$
\begin{align*}
\dot{q}&=\frac{p}{m}\\
\dot{p}&=F(q)-\frac{p_{\eta_1}}{Q_1}p-\frac{p_{\eta_1}}{Q_2}\left[(k_{\rm B}T)p+\frac{p^3}{3m}\right]\\
\dot{\eta}_1&=\frac{p_{\eta_1}}{Q_1}\\
\dot{\eta}_2&=\left[(k_{\rm B}T)+\frac{p^2}{m}\right]\frac{p_{\eta_2}}{Q_2}\\
\dot{p}_{\eta_1}&=\frac{p^2}{m}-k_{\rm B}T\\
\dot{p}_{\eta_2}&=\frac{p^4}{3m^2}-(k_{\rm B}T)^2
\end{align*}
$$
a. これらの運動方程式がハミルトン系ではないことを示せ。
b. 以下のエネルギーが保存されることを示せ。
$$
\begin{align*}
\mathcal{H}'&=\frac{p^2}{2m}+U(q)+\frac{p_{\eta_1}^2}{2Q_1}+\frac{p_{\eta_2}^2}{2Q_2}+k_{\rm B}T(\eta_1+\eta_2)
\end{align*}
$$
c. 4.9節におけるハミルトン系ではない場合の形式化を用いることにより,これらの運動方程式が物理的なハミルトニアン$${\mathcal{H}=p^2/2m+U(q)}$$のカノニカル分布を生成することを示せ。
d. これらの運動方程式はマクスウェル-ボルツマン分布$${P(p)\propto\exp(-\beta p^2/2m)}$$の2次モーメントまでで揺らぎを調整するよう設計されている。モーメントの任意の次数$${M}$$を扱う方程式は以下の通りとなる。
$$
\begin{align*}
\dot{q}&=\frac{p}{m}\\
\dot{p}&=F(q)-\sum_{n=1}^M\sum_{k=1}^n\frac{p_{\eta_n}}{Q_n}\frac{(k_{\rm B}T)^{n-k}}{C_{k-1}}\frac{p^{2k-1}}{m^{k-1}}\\
\dot{\eta}_n&=\left[(k_{\rm B}T)^{n-1}+\sum_{k=2}^n\frac{(k_{\rm B}T)^{n-k}}{C_{k-2}}\left(\frac{p^2}{m}\right)^{k-1}\right]\frac{p_{\eta_n}}{Q_n}\\
\dot{p}_{\eta_n}&=\frac{1}{C_{n-1}}\left(\frac{p^2}{m}\right)^n-(k_{\rm B}T)^n
\end{align*}
$$
ここで,$${C_n=\prod_{k=1}^n(1+2k), C_0:=1}$$である。
これらの方程式(及びN粒子系への拡張)はLiuとTuckermanによって初めて導入された。
この場合,以下のエネルギーが保存されること,及び$${\mathcal{H}=p^2/2m+U(q)}$$のカノニカル分布が生成されることを示せ。
$$
\begin{align*}
\mathcal{H}'&=\frac{p^2}{2m}+U(q)+\sum_{n=1}^M\frac{p_{\eta_n}^2}{2Q_n}+k_{\rm B}T\sum_{n=1}^M\eta_n
\end{align*}
$$
a. $${\mathbf{x}:=\begin{bmatrix}q& p & \eta_1& \eta_2&p_{\eta_1}&p_{\eta_2}\end{bmatrix}^{\rm T}}$$とおくと,
$$
\begin{align*}
\nabla_{\mathbf{x}}\cdot\dot{\mathbf{x}}&=-\frac{p_{\eta_1}}{Q_1}-\frac{p_{\eta_2}}{Q_2}\left[k_{\rm B}T+\frac{p^2}{m}\right]\\
&=-(\dot{\eta}_1+\dot{\eta}_2)\\
&\neq 0
\end{align*}
$$
となるため,この系はハミルトン系ではない。
b.
$$
\begin{align*}
\frac{{\rm d}\mathcal{H}'}{{\rm d}t}&=\frac{p\dot{p}}{m}+\frac{\partial U}{\partial q}\dot{q}+\frac{p_{\eta_1}\dot{p}_{\eta_1}}{Q_1}+\frac{p_{\eta_2}\dot{p}_{\eta_2}}{Q_2}+k_{\rm B}T(\dot{\eta}_1+\dot{\eta}_2)\\
&=\frac{p\dot{p}}{m}-F(q)\dot{q}+\frac{p_{\eta_1}\dot{p}_{\eta_1}}{Q_1}+\frac{p_{\eta_2}\dot{p}_{\eta_2}}{Q_2}+k_{\rm B}T(\dot{\eta}_1+\dot{\eta}_2)\\
&=\frac{p}{m}\left(F(q)-\frac{p_{\eta_1}}{Q_1}p-\frac{p_{\eta_1}}{Q_2}\left[(k_{\rm B}T)p+\frac{p^3}{3m}\right]\right)-F(q)\frac{p}{m}+\frac{p_{\eta_1}}{Q_1}\left(\frac{p^2}{m}-k_{\rm B}T\right)+\frac{p_{\eta_2}}{Q_2}\left(\frac{p^4}{3m^2}-(k_{\rm B}T)^2\right)+k_{\rm B}T\left(\frac{p_{\eta_1}}{Q_1}+\left[(k_{\rm B}T)+\frac{p^2}{m}\right]\frac{p_{\eta_2}}{Q_2}\right)\\
&=0
\end{align*}
$$
c. $${\kappa=-(\dot{\eta}_1+\dot{\eta}_2)=\dot{w}}$$より,$${\sqrt{g}=\exp(-w)=\exp(\eta_1+\eta_2)}$$となる。
$${E:=\mathcal{H}'(\mathbf{x})}$$として全系に対する分配関数を計算すると,
$$
\begin{align*}
\mathcal{Z}&=\int{\rm d}\mathbf{x}\sqrt{g}\delta(\mathcal{H}'(\mathbf{x})-E) \\
&=\int{\rm d}\mathbf{x}\exp(\eta_1+\eta_2)\delta\left(\frac{p^2}{2m}+U(q)+\frac{p_{\eta_1}^2}{2Q_1}+\frac{p_{\eta_2}^2}{2Q_2}+k_{\rm B}T(\eta_1+\eta_2)-E\right) \\
&=\int{\rm d}q\int{\rm d}p\int{\rm d}\eta_1\int{\rm d}p_{\eta_1}\int{\rm d}p_{\eta_2}\exp(\eta_1)\exp\left(\frac{E-\left(\frac{p^2}{2m}+U(q)+\frac{p_{\eta_1}^2}{2Q_1}+\frac{p_{\eta_2}^2}{2Q_2}\right)}{k_{\rm B}T}-\eta_1\right)\\
&=\left\{\exp\left(\frac{E}{k_{\rm B}T}\right)\int{\rm d}\eta_1\int{\rm d}p_{\eta_1}\exp\left(-\frac{p_{\eta_1}^2}{2Q_1k_{\rm B}T}\right)\int{\rm d}p_{\eta_1}\exp\left(-\frac{p_{\eta_2}^2}{2Q_2k_{\rm B}T}\right)\right\}\int{\rm d}q\int{\rm d}p\exp\left(-\frac{\frac{p^2}{2m}+U(q)}{k_{\rm B}T}\right)\\
\therefore \mathcal{Z}&\propto\int{\rm d}q\int{\rm d}p\exp\left(-\frac{\mathcal{H}(q,p)}{k_{\rm B}T}\right)
\end{align*}
$$
d.
$$
\begin{align*}
\frac{{\rm d}\mathcal{H}'}{{\rm d}t}&=\frac{p\dot{p}}{m}-F(q)\dot{q}+\sum_{n=1}^M\frac{p_{\eta_n}\dot{p}_{\eta_n}}{Q_n}+k_{\rm B}T\sum_{n=1}^M\dot{\eta}_n\\
&=\frac{p}{m}\left\{F(q)-\sum_{n=1}^M\sum_{k=1}^n\frac{p_{\eta_n}}{Q_n}\frac{(k_{\rm B}T)^{n-k}}{C_{k-1}}\frac{p^{2k-1}}{m^{k-1}}\right\}-F(q)\frac{p}{m}+\sum_{n=1}^M\frac{p_{\eta_n}}{Q_n}\left\{\frac{1}{C_{n-1}}\left(\frac{p^2}{m}\right)^n-(k_{\rm B}T)^n\right\}+k_{\rm B}T\sum_{n=1}^M\left[(k_{\rm B}T)^{n-1}+\sum_{k=2}^n\frac{(k_{\rm B}T)^{n-k}}{C_{k-2}}\left(\frac{p^2}{m}\right)^{k-1}\right]\frac{p_{\eta_n}}{Q_n}\\
&=-\sum_{n=1}^M\sum_{k=1}^n\frac{p_{\eta_n}}{Q_n}\frac{(k_{\rm B}T)^{n-k}}{C_{k-1}}\frac{p^{2k}}{m^{k}}+\sum_{n=1}^M\frac{p_{\eta_n}}{Q_n}\left\{\frac{1}{C_{n-1}}\left(\frac{p^2}{m}\right)^n-(k_{\rm B}T)^n\right\}+\sum_{n=1}^M\left[(k_{\rm B}T)^{n}+\sum_{k=1}^{n-1}\frac{(k_{\rm B}T)^{n-k}}{C_{k-1}}\left(\frac{p^2}{m}\right)^{k}\right]\frac{p_{\eta_n}}{Q_n}\\
&=-\sum_{n=1}^M\frac{p_{\eta_n}}{Q_n}\frac{1}{C_{n-1}}\frac{p^{2n}}{m^{n}}+\sum_{n=1}^M\frac{p_{\eta_n}}{Q_n}\frac{1}{C_{n-1}}\left(\frac{p^2}{m}\right)^n\\
&=0
\end{align*}
$$
$${\sqrt{g}=\exp(\sum_{n=1}^M\eta_n)}$$より,
$$
\begin{align*}
\mathcal{Z}&=\int{\rm d}\mathbf{x}\sqrt{g}\delta(\mathcal{H}'(\mathbf{x})-E) \\
&=\int{\rm d}\mathbf{x}\exp\left(\sum_{n=1}^M\eta_n\right)\delta\left(\frac{p^2}{2m}+U(q)+\sum_{n=1}^M\frac{p_{\eta_n}^2}{2Q_n}+k_{\rm B}T\sum_{n=1}^M\eta_n-E\right) \\
&=\int{\rm d}q\int{\rm d}p\left(\prod_{n=1}^{M-1}\int{\rm d}\eta_n\right)\left(\prod_{n=1}^{M}\int{\rm d}p_{\eta_n}\right)\exp\left(\sum_{n=1}^{M-1}\eta_n\right)\exp\left(\frac{E-\left(\frac{p^2}{2m}+U(q)+\sum_{n=1}^M\frac{p_{\eta_n}^2}{2Q_n}\right)}{k_{\rm B}T}-\sum_{n=1}^{M-1}\eta_n\right)\\
&=\left\{\exp\left(\frac{E}{k_{\rm B}T}\right)\left(\prod_{n=1}^{M-1}\int{\rm d}\eta_n\right)\left(\prod_{n=1}^{M}\int{\rm d}p_{\eta_n}\exp\left(-\frac{p_{\eta_n}^2}{2Q_nk_{\rm B}T}\right)\right)\right\}\int{\rm d}q\int{\rm d}p\exp\left(-\frac{\frac{p^2}{2m}+U(q)}{k_{\rm B}T}\right)\\
\therefore \mathcal{Z}&\propto\int{\rm d}q\int{\rm d}p\exp\left(-\frac{\mathcal{H}(q,p)}{k_{\rm B}T}\right)
\end{align*}
$$
Problem 4.3
a. 一次元運動する質量$${m}$$の単粒子に対するNose–Hoover方程式を考える。運動方程式は以下のとおりである。
$$
\begin{align*}
\dot{p}&=-\frac{p_{\eta}}{Q}p\\
\dot{\eta}&=\frac{p_{\eta}}{Q}\\
\dot{p}_{\eta}&=\frac{p^2}{m}-k_{\rm B}T
\end{align*}
$$
これらの方程式が以下の2つの保存則に従うことを示せ。
$$
\begin{align*}
C&=\frac{p^2}{2m}+\frac{p_{\eta}^2}{2Q}+k_{\rm B}T\eta&=:\mathcal{H}'\\
K&=p{\rm e}^{\eta}
\end{align*}
$$
b. 物理的な運動量$${p}$$の分布関数は
$$
\begin{align*}
f(p)&=\frac{\sqrt{2Q}}{\sqrt{p^2(C-(p^2/2m)+k_{\rm B}T\ln(p/K))}}
\end{align*}
$$
となり,マクスウェル-ボルツマン分布とは異なることを示せ。
参考までにマクスウェル-ボルツマン分布の場合は以下の式で表される。
$$
\begin{align*}
f(p)&=\frac{1}{\sqrt{2\pi m k_{\rm B}T}}\exp(-p^2/2mk_{\rm B}T)
\end{align*}
$$
c. $${f(p)}$$の分布をプロットし,図4.9で示される分布と一致することを示せ。

d. 節4.11のアルゴリズムを用いて運動方程式を積分するプログラムを書き,数値計算で得られる分布がcでプロットした分布に一致することを確かめよ。
e. 次に,同じ単粒子に対して$${M=2}$$の場合のNose-Hoover chain方程式を考える。
$$
\begin{align*}
\dot{p}&=-\frac{p_{\eta_1}}{Q}p\\
\dot{\eta}_k&=\frac{p_{\eta_k}}{Q}\\
\dot{p}_{\eta_1}&=\frac{p^2}{m}-k_{\rm B}T-\frac{p_{\eta_2}}{Q}p_{\eta_1}\\
\dot{p}_{\eta_2}&=\frac{p_{\eta_1}^2}{Q}-k_{\rm B}T
\end{align*}
$$
ここで,$${k=1,2}$$である。これらの運動方程式は$${p}$$に対してマクスウェル-ボルツマン分布を生成することを示せ。
f. 節4.11のリウヴィルベースの積分法を用いて実装した場合,数値計算でマクスウェル-ボルツマン分布を正確に生成することができるであろうか?
ヒント:$${p(0)>0}$$,もしくは$${p(0)<0}$$の場合にどのように時間発展するかを考えよ
g. 外力がなく,式(4.9.27)の保存則に従う場合,式(4.8.19)で生成される一般分布を導出せよ。
$$
\begin{align*}
\dot{\mathbf{r}}_i&=\frac{\mathbf{p}_i}{m_i}\\
\dot{\mathbf{p}}_i&=\mathbf{F}_i-\frac{p_{\eta}}{Q}\mathbf{p}_i\\
\dot{\eta}&=\frac{p_{\eta}}{Q}\\
\dot{p}_{\eta}&=\sum_{i=1}^N\frac{\mathbf{p}_i^2}{m_i}-dNk_{\rm B}T
\end{align*}\tag{4.8.19}
$$
$$
\begin{align*}
\mathbf{P}{\rm e}^{\eta}&=\mathbf{K}
\end{align*}\tag{4.9.27}
$$
ヒント:保存則は重心運動量$${\mathbf{P}}$$に関するものであるため,重心運動量,座標$${(\mathbf{R}, \mathbf{P})}$$と$${d(N-1)}$$個の相対座標$${\mathbf{r}_1',\mathbf{r}_2',\cdots}$$と相対運動量$${\mathbf{p}_1',\mathbf{p}_2',\cdots}$$の正準変換を導入するのが有効である。
h. $${\sum_{i=1}^N\mathbf{F}_i=\mathbf{0}}$$のとき,Nose-Hoover chain方程式は重心運動量以外の全変数に対して正確なカノニカル分布を生成することを示せ。
i. 最後に,式(4.10.7)の場合は$${\sum_{i=1}^N\mathbf{F}_i=\mathbf{0}}$$にであったとしても運動量に関する保存則が成立しないことを示せ。つまり,この場合は全変数に対して正確なカノニカル分布が生成されることになる。
$$
\begin{align*}
\dot{\mathbf{r}}_i&=\frac{\mathbf{p}_i}{m_i}\\
\dot{\mathbf{p}}_i&=\mathbf{F}_i-\frac{p_{\eta_1,i}}{Q_1}\mathbf{p}_i\\
\dot{\eta}_{j,i}&=\frac{p_{\eta_{j,i}}}{Q_j}&j=1,\cdots,M\\
\dot{p}_{\eta_{1,i}}&=\left[\frac{\mathbf{p}_i^2}{m_i}-dk_{\rm B}T\right]-\frac{p_{\eta_{j+1,i}}}{Q_{j+1}}p_{\eta_j}\\
\dot{p}_{\eta_{j,i}}&=\left[\frac{p_{\eta_{j-1,i}}^2}{Q_{j-1}}-k_{\rm B}T\right]-\frac{p_{\eta_{j+1,i}}}{Q_{j+1}}p_{\eta_j}&j=2,\cdots,M-1\\
\dot{p}_{\eta_{M,i}}&=\left[\frac{p_{\eta_{M-1,i}}^2}{Q_{M-1}}-k_{\rm B}T\right]
\end{align*}\tag{4.10.7}
$$
a.
$$
\begin{align*}
\dot{C}&=\frac{p}{m}\dot{p}+\frac{p_{\eta}}{Q}\dot{p}_{\eta}+k_{\rm B}T\dot{\eta}\\
&=\frac{p}{m}\left(-\frac{p_{\eta}}{Q}p\right)+\frac{p_{\eta}}{Q}\left(\frac{p^2}{m}-k_{\rm B}T\right)+k_{\rm B}T\frac{p_{\eta}}{Q}\\
&=0\\
\dot{K}&=\left(\dot{p}+p\dot{\eta}\right){\rm e}^{\eta}\\
&=\left(-\frac{p_{\eta}}{Q}p+p\frac{p_{\eta}}{Q}\right){\rm e}^{\eta}\\
&=0
\end{align*}
$$
b. $${\nabla_{\mathbf{x}}\cdot\dot{\mathbf{x}}=-p_{\eta}/Q=-\dot{\eta}\rightarrow \sqrt{g}=\exp(-w)=\exp(\eta)}$$より,
$$
\begin{align*}
f(p)&=\int{\rm d}\eta\int{\rm d}p_{\eta}\exp(\eta)\delta\left(\frac{p^2}{2m}+\frac{p_{\eta}^2}{2Q}+k_{\rm B}T\eta-C\right)\delta\left(p{\rm e}^{\eta}-K\right)\\
&=\int{\rm d}\eta\int{\rm d}p_{\eta}\exp(\eta)\frac{Q}{\sqrt{2Q\left(C-\frac{p^2}{2m}-k_{\rm B}T\eta\right)}}\left\{\delta\left(p_{\eta}-\sqrt{2Q\left(C-\frac{p^2}{2m}-k_{\rm B}T\eta\right)}\right)+\delta\left(p_{\eta}+\sqrt{2Q\left(C-\frac{p^2}{2m}-k_{\rm B}T\eta\right)}\right)\right\}\frac{\delta\left(\eta-\ln(K/p)\right)}{K}\\
&=\int{\rm d}\eta\exp(\eta)\frac{2Q\delta\left(\eta-\ln(K/p)\right)}{K\sqrt{2Q\left(C-\frac{p^2}{2m}-k_{\rm B}T\eta\right)}}\\
&=\frac{2Q}{p\sqrt{2Q\left(C-\frac{p^2}{2m}+k_{\rm B}T\ln(p/K)\right)}}\\
&=\frac{\sqrt{2Q}}{\sqrt{p^2\left(C-\frac{p^2}{2m}+k_{\rm B}T\ln(p/K)\right)}}\\
\end{align*}
$$
c. & d. $${\mathbf{x}:=\begin{bmatrix}p&\eta&p_{\eta}\end{bmatrix}^{\rm T}}$$に対して,
$$
\begin{align*}
{\rm i}\mathcal{L}&=\dot{\mathbf{x}}\cdot\nabla_{\mathbf{x}}\\
&=-\frac{p_{\eta}}{Q}p\frac{\partial}{\partial p}+\frac{p_{\eta}}{Q}\frac{\partial}{\partial \eta}+\left(\frac{p^2}{m}-k_{\rm B}T\right)\frac{\partial}{\partial p_{\eta}}\\
&={\rm i}\mathcal{L}_{1}+{\rm i}\mathcal{L}_{\rm NH}\\
{\rm i}\mathcal{L}_{1}&:=-\frac{p_{\eta}}{Q}p\frac{\partial}{\partial p}\\
{\rm i}\mathcal{L}_{\rm NH}&:=\frac{p_{\eta}}{Q}\frac{\partial}{\partial \eta}+\left(\frac{p^2}{m}-k_{\rm B}T\right)\frac{\partial}{\partial p_{\eta}}
\end{align*}
$$
と定義し,以下の時間発展演算子を用いて数値積分することを考える。
$$
\begin{align*}
\exp\left({\rm i}\mathcal{L}\Delta t\right)&\simeq\exp\left({\rm i}\mathcal{L}_{\rm NH}\frac{\Delta t}{2}\right)\exp\left({\rm i}\mathcal{L}_1\Delta t\right)\exp\left({\rm i}\mathcal{L}_{\rm NH}\frac{\Delta t}{2}\right)
\end{align*}
$$
上記の時間発展演算子を用いた場合,$${t\rightarrow t+\Delta t}$$に対する位相空間ベクトルの更新は
$$
\begin{align*}
\begin{bmatrix}p(t+\Delta t)\\\eta(t+\Delta t)\\ p_{\eta}(t+\Delta t)\end{bmatrix}&=\begin{bmatrix}p(t)-\frac{p_{\eta}\left(t+\frac{\Delta t}{2}\right)}{Q}p(t)\Delta t\\\eta\left(t+\frac{\Delta t}{2}\right)+\frac{p_{\eta}\left(t+\frac{\Delta t}{2}\right)}{Q}\frac{\Delta t}{2}\\ p_{\eta}\left(t+\frac{\Delta t}{2}\right)+\left\{\frac{p(t+\Delta t)^2}{m}-k_{\rm B}T \right\}\frac{\Delta t}{2}\end{bmatrix}\\
\eta\left(t+\frac{\Delta t}{2}\right)&=\eta(t)+\frac{p_{\eta}(t)}{Q}\frac{\Delta t}{2}\\
p_{\eta}\left(t+\frac{\Delta t}{2}\right)&=p_{\eta}\left(t\right)+\left\{\frac{p(t)^2}{m}-k_{\rm B}T \right\}\frac{\Delta t}{2}
\end{align*}
$$
となる。
pythonによるサンプルコードを以下に示す。
import numpy as np
import matplotlib.pyplot as plt
# Parameters
kT = 1
m = 1
Q = 1e-1
dt = 1e-3
n_step = 10000
p_ini = 1
eta_ini = 0
p_eta_ini = 0.1
# Define functions
def f(x, C_f, K_f):
if x == 0:
return 0
a = C_f - 0.5 * x ** 2 / m + kT * np.log(x / K_f)
if a > 0:
return np.sqrt(2 * Q) / np.sqrt(x ** 2 * a)
else:
return 0
def C(p, eta, p_eta):
return 0.5 * p ** 2 / m + 0.5 * p_eta ** 2 / Q + kT * eta
def K(p, eta):
return p * np.exp(eta)
# --- below is the code --- #
# Plot the analytical solution of f(p)
C_ini = C(p_ini, eta_ini, p_eta_ini)
K_ini = K(p_ini, eta_ini)
x = np.linspace(0, 2, 100)
y = [f(p, C_ini, K_ini) for p in x]
x = np.concatenate([np.flip(-x), x])
y = np.concatenate([np.flip(y), y])
plt.plot(x,y)
plt.xlabel("p")
plt.ylabel("f(p)")
plt.savefig("f(p)_ana.png")
plt.figure()
#-------------------------------------------------#
# Integrate the equations of motion and sample p values numerically
p_list = [p_ini]
eta_list = [eta_ini]
p_eta_list = [p_eta_ini]
C_list = [C_ini]
K_list = [K_ini]
for i in range(n_step):
eta_half = eta_list[-1] + 0.5 * p_eta_list[-1] * dt / Q
p_eta_half = p_eta_list[-1] + 0.5 * (p_list[-1] ** 2 / m - kT) * dt
p_list.append(p_list[-1] - p_eta_half * p_list[-1] * dt / Q)
eta_list.append(eta_half + 0.5 * p_eta_half * dt / Q)
p_eta_list.append(p_eta_half + 0.5 * (p_list[-1] ** 2 / m - kT) * dt)
C_list.append(C(p_list[-1], eta_list[-1], p_eta_list[-1]))
K_list.append(K(p_list[-1], eta_list[-1]))
header = 'i, p, eta, p_eta, C, K'
result = np.array([np.arange(len(p_list)), p_list, eta_list, p_eta_list, C_list, K_list]).T
with open('result.csv', 'wb') as f:
np.savetxt(f, result, header = header, delimiter=",")
plt.hist(p_list, density = True, bins=101)
plt.xlabel("p")
plt.ylabel("f(p)")
plt.xlim([0,2])
plt.savefig("f(p)_numerical.png")
plt.figure()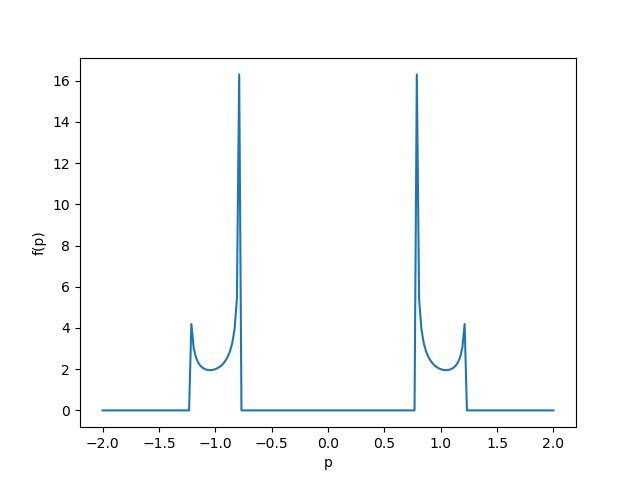

e.
$$
\begin{align*}
f(p)&=\int{\rm d}\eta_1\int{\rm d}\eta_2\int{\rm d}p_{\eta_1}\int{\rm d}p_{\eta_2}{\rm e}^{\eta_1+\eta_2}\delta\left(\frac{p^2}{2m}+\frac{p_{\eta_1}^2+p_{\eta_2}^2}{2Q}+k_{\rm B}T(\eta_1+\eta_2)-C\right)\delta\left(p{\rm e}^{\eta_1}-K\right)\\
&=4\pi Q\int{\rm d}\eta_1\int{\rm d}\eta_2\int{\rm d}p_r{\rm e}^{\eta_1+\eta_2}\delta\left(\frac{p^2}{2m}+p_r^2+k_{\rm B}T(\eta_1+\eta_2)-C\right)\delta\left(p{\rm e}^{\eta_1}-K\right)\\
&=2\pi Q\int{\rm d}\eta_1\int{\rm d}\eta_2\int{\rm d}p_{r}{\rm e}^{\eta_1+\eta_2}\frac{\delta\left(p_r-\sqrt{C-\left(\frac{p^2}{2m}+k_{\rm B}T(\eta_1+\eta_2)\right)}\right)}{\sqrt{C-\left(\frac{p^2}{2m}+k_{\rm B}T(\eta_1+\eta_2)\right)}}\frac{\delta\left(\eta_1-\ln(K/p)\right)}{K}\\
&=\frac{2\pi Q}{K}\int{\rm d}\eta_1\int{\rm d}\eta_2\frac{{\rm e}^{\eta_1+\eta_2}\delta\left(\eta_1-\ln(K/p)\right)}{\sqrt{C-\left(\frac{p^2}{2m}+k_{\rm B}T(\eta_1+\eta_2)\right)}}\\
&=\frac{2\pi Q}{p}\int{\rm d}\eta_2\frac{{\rm e}^{\eta_2}}{\sqrt{C-\left(\frac{p^2}{2m}+k_{\rm B}T(\ln(K/p)+\eta_2)\right)}}\\
&=\frac{2\pi Q}{p\sqrt{k_{\rm B}T}}\int_{-\infty}^{\frac{C-\frac{p^2}{2m}}{k_{\rm B}T}-\ln(K/p)}{\rm d}\eta_2\frac{{\rm e}^{\eta_2}}{\sqrt{\left(\frac{C-\frac{p^2}{2m}}{k_{\rm B}T}-\ln(K/p)\right)-\eta_2}}\\
&=\frac{2\pi Q}{p\sqrt{k_{\rm B}T}}\exp\left(\frac{C-\frac{p^2}{2m}}{k_{\rm B}T}-\ln(K/p)\right)\left(\Gamma\left(\frac{1}{2},0\right)-\Gamma\left(\frac{1}{2},\infty\right)\right)\\
&=\frac{2\pi Q\exp\left(\frac{C}{k_{\rm B}T}\right)}{K\sqrt{k_{\rm B}T}}\exp\left(-\frac{{p^2}}{2mk_{\rm B}T}\right)\\
&\propto \frac{\exp\left(-\frac{{p^2}}{2mk_{\rm B}T}\right)}{\sqrt{2\pi mk_{\rm B}T}}
\end{align*}
$$
f. $${p{\rm e}^{\eta_1}=K}$$が保存するため,$${p(0)>0}$$から時間発展した場合,$${p(t)<0}$$となることは(数値計算上で$${K}$$の保存則が著しく破綻しない限り)ない。$${p(0)<0}$$についても同様である。
g. 以下の相対座標を考える。
$$
\begin{align*}
\mathbf{R}&:=\frac{\sum_{i=1}^Nm_i\mathbf{r}_i}{\sum_{i=1}^Nm_i}\\
&=:\frac{\sum_{i=1}^Nm_i\mathbf{r}_i}{M}\\
\mathbf{r}_k'&:=\mathbf{r}_k-\frac{\sum_{l=1}^Nm_i\mathbf{r}_i}{\sum_{l=1}^{k-1}m_l}\ \ \ \ {\rm for}\ k=2,\cdots,N\\
&=:\mathbf{r}_k-\frac{\sum_{l=1}^Nm_i\mathbf{r}_i}{m_k'}\\
\end{align*}
$$
対応する正準運動量は以下のようになる。
$$
\begin{align*}
\mathbf{P}&:=M\dot{\mathbf{R}}\\
\mathbf{p}_k'&:=\mu_k\dot{\mathbf{r}}_k'\ \ \ \ {\rm for}\ k=2,\cdots,N\\
\mu_k&:=\frac{m_{k-1}'m_k}{m_k'}
\end{align*}
$$
相対座標とその正準共役な運動量を用いた場合,nose-hooverの分配関数$${\mathcal{Z}}$$は以下の式で与えられる。
$$
\begin{align*}
\mathcal{Z}&=\int{\rm d}^{N-1}\mathbf{r}'\int{\rm d}^{N-1}\mathbf{p}'\int{\rm d}\mathbf{R}\int{\rm d}\mathbf{P}\int{\rm d}\eta\int{\rm d}p_{\eta}{\rm e}^{-dN\eta}\delta\left(\frac{1}{2M}\mathbf{P}^2+\mathcal{H}(\mathbf{r}',\mathbf{p}')+\frac{p_{\eta}^2}{2Q}+dNk_{\rm B}T\eta-\mathcal{H}'\right)\delta\left(\mathbf{P}{\rm e}^{\eta}-\mathbf{K}\right)\\
&=V\int{\rm d}^{N-1}\mathbf{r}'\int{\rm d}^{N-1}\mathbf{p}'\int{\rm d}\eta\int{\rm d}p_{\eta}{\rm e}^{-d(N-1)\eta}\delta\left(\mathcal{H}(\mathbf{r}',\mathbf{p}')+\frac{\mathbf{K}^2{\rm e}^{-2\eta}}{2M}+\frac{p_{\eta}^2}{2Q}+dNk_{\rm B}T\eta-\mathcal{H}'\right)\\
\end{align*}
$$
h. サイズ$${M}$$のNose-Hoover chainの分配関数をg. の場合と同様に相対座標とその正準共役な運動量を用いて計算すると,
$$
\begin{align*}
\mathcal{Z}&=\int{\rm d}^{N-1}\mathbf{r}'\int{\rm d}^{N-1}\mathbf{p}'\int{\rm d}\mathbf{R}\int{\rm d}\mathbf{P}\left\{\prod_{j=1}^M\int{\rm d}\eta_j\right\}\left\{\prod_{j=1}^M\int{\rm d}p_{\eta_j}\right\}{\rm e}^{dN\eta+\sum_{j=2}^M\eta_j}\delta\left(\mathcal{H}(\mathbf{r}',\mathbf{p}')+\frac{\mathbf{P}^2}{2M}+\sum_{j=1}^M\frac{p_{\eta_j}^2}{2Q_j}+dNk_{\rm B}T\eta_1+k_{\rm B}T\sum_{j=2}^M\eta_j-\mathcal{H}'\right)\delta\left(\mathbf{P}{\rm e}^{\eta_1}-\mathbf{K}\right)\\
&=V\int{\rm d}^{N-1}\mathbf{r}'\int{\rm d}^{N-1}\mathbf{p}'\int{\rm d}\mathbf{P}\left\{\prod_{j=1}^M\int{\rm d}\eta_j\right\}\left\{\prod_{j=1}^M\int{\rm d}p_{\eta_j}\right\}{\rm e}^{dN\eta+\sum_{j=2}^M\eta_j}\delta\left(\mathcal{H}(\mathbf{r}',\mathbf{p}')+\frac{\mathbf{P}^2}{2M}+\sum_{j=1}^M\frac{p_{\eta_j}^2}{2Q_j}+dNk_{\rm B}T\eta_1+k_{\rm B}T\sum_{j=2}^M\eta_j-\mathcal{H}'\right)\delta\left(\mathbf{P}{\rm e}^{\eta_1}-\mathbf{K}\right)\\
&=\frac{V}{k_{\rm B}T}\int{\rm d}^{N-1}\mathbf{r}'\int{\rm d}^{N-1}\mathbf{p}'\int{\rm d}\mathbf{P}\left\{\prod_{j=1}^{M-1}\int{\rm d}\eta_j\right\}\left\{\prod_{j=1}^M\int{\rm d}p_{\eta_j}\right\}\exp\left(-\frac{\mathcal{H}(\mathbf{r}',\mathbf{p}')+\frac{\mathbf{P}^2}{2M}+\sum_{j=1}^M\frac{p_{\eta_j}^2}{2Q_j}-\mathcal{H}'}{k_{\rm B}T}\right)\delta\left(\mathbf{P}{\rm e}^{\eta_1}-\mathbf{K}\right)\\
&=\frac{V^{\frac{M+1}{3}}\exp\left(\frac{\mathcal{H}'}{k_{\rm B}T}\right)}{k_{\rm B}T}\left\{\prod_{j=1}^M\int{\rm d}p_{\eta_j}\exp\left(-\frac{p_{\eta_j}^2}{2Q_jk_{\rm B}T}\right)\right\}\int{\rm d}^{N-1}\mathbf{r}'\int{\rm d}^{N-1}\mathbf{p}'\int{\rm d}\eta_1\exp\left(-\frac{\mathcal{H}(\mathbf{r}',\mathbf{p}')+\frac{\mathbf{K}^2{\rm e}^{2\eta_1}}{2M}+dk_{\rm B}T\eta_1}{k_{\rm B}T}\right)\\
&=\left[\frac{V^{\frac{M+1}{3}}\exp\left(\frac{\mathcal{H}'}{k_{\rm B}T}\right)}{k_{\rm B}T}\left\{\prod_{j=1}^M\sqrt{2\pi Q_j k_{\rm B}T}\right\}\left\{\int{\rm d}\eta_1\exp\left(-\frac{\frac{\mathbf{K}^2{\rm e}^{2\eta_1}}{2M}+dk_{\rm B}T\eta_1}{k_{\rm B}T}\right)\right\}\right]\int{\rm d}^{N-1}\mathbf{r}'\int{\rm d}^{N-1}\mathbf{p}'\exp\left(-\frac{\mathcal{H}(\mathbf{r}',\mathbf{p}')}{k_{\rm B}T}\right)\\
&\propto \int{\rm d}^{N-1}\mathbf{r}'\int{\rm d}^{N-1}\mathbf{p}'\exp\left(-\frac{\mathcal{H}(\mathbf{r}',\mathbf{p}')}{k_{\rm B}T}\right)
\end{align*}
$$
i.
$$
\begin{align*}
\frac{{\rm d}}{{\rm d}t}\left(\mathbf{P}{\rm e}^{\eta_{j,i}}\right)&=\left(\dot{\mathbf{P}}+\dot{\eta}_{j,i}\mathbf{P}\right){\rm e}^{\eta_{j,i}}\\
&=\left\{\sum_{k=1}^N\left(\mathbf{F}_k-\frac{p_{\eta_{1,k}}}{Q_1}\mathbf{p}_k\right)+\frac{p_{\eta_{j,i}}}{Q_j}\sum_{k=1}^N\mathbf{p}_k\right\}{\rm e}^{\eta_{j,i}}\\
\end{align*}
$$
より,$${\mathbf{P}{\rm e}^{\eta_{j,i}}}$$はたとえ$${\sum_{k=1}^N\mathbf{F}_k=\mathbf{0}}$$であっても一般的には保存しない。これだけでは運動量に関する保存量が存在しない証明をしたことにはならないが,少なくとも前問まででは存在したような保存量はなさそうである。
Problem 4.4
単位質量,単位振動数,かつ$${k_{\rm B}T=1}$$の場合の調和振動子に対する修正されたNose-Hoover方程式を考える。
$$
\begin{align*}
\dot{x}&=p-p_{\eta}x\\
\dot{p}&=-x-p_{\eta}p\\
\dot{\eta}&=p_{\eta}\\
p_{\eta}&=p^2+x^2-2
\end{align*}
$$
a. これらの方程式には以下の2つの保存則が存在することを示せ。
$$
\begin{align*}
C&=\frac{1}{2}(p^2+x^2+p_{\eta}^2)+2\eta\\
K&=\frac{1}{2}(p^2+x^2){\rm e}^{2\eta}
\end{align*}
$$
b. 物理的なハミルトニアン$${\mathcal{H}(x,p)=(p^2+x^2)/2}$$の分布関数$${f(H)}$$を決定せよ。$${f(H)}$$はカノニカル分布になる($${f(H)\propto\exp(-H)}$$)であろうか?
ヒント:2つの保存則を用いて変数$${\eta, p_{\eta}}$$を消去することを考えよ。
c. 位相空間上で軌跡をプロットした際に$${(x,p)=(0,0)}$$付近にホール(状態が存在しない領域)が存在することを示し,またホールのサイズを決める条件を求めよ。
$$
\begin{align*}
\dot{C}&=\dot{p}p+\dot{x}x+\dot{p}_{\eta}p_{\eta}+2\dot{\eta}\\
&=\left(-x-p_{\eta}p\right)p+\left(p-p_{\eta}x\right)x+\left(p^2+x^2-2\right)p_{\eta}+2\left(p_{\eta}\right)\\
&=0\\
\dot{K}&=(\dot{p}p+\dot{x}x){\rm e}^{2\eta}+(p^2+x^2)\dot{\eta}{\rm e}^{2\eta}\\
&=\left[\left\{\left(-x-p_{\eta}p\right)p+\left(p-p_{\eta}x\right)x\right\}+(p^2+x^2)\left(p_{\eta}\right)\right]{\rm e}^{2\eta}\\
&=0
\end{align*}
$$
b. $${\mathbf{x}:=\begin{bmatrix}x&p&\eta&p_{\eta}\end{bmatrix}}$$とおくと,
$$
\begin{align*}
\nabla_{\mathbf{x}}\cdot\dot{\mathbf{x}}&=-p_{\eta}\\
&=-\dot{\eta}\\
&=\dot{w}\\
\therefore \sqrt{g}&=\exp(-w)&=\exp(\eta)
\end{align*}
$$
$${C,K}$$の保存量を考慮して全変数に対する分配関数$${\mathcal{Z}}$$を計算すると,
$$
\begin{align*}
\mathcal{Z}&=\int{\rm d}\mathbf{x}\exp(\eta)\delta\left(\frac{1}{2}(p^2+x^2+p_{\eta}^2)+2\eta-C\right)\delta\left(\frac{1}{2}(p^2+x^2){\rm e}^{2\eta}-K\right)\\
&=\int{\rm d}\mathbf{x}\exp(\eta)\frac{\delta\left(p_{\eta}-\sqrt{2C-4\eta-p^2-x^2}\right)+\delta\left(p_{\eta}+\sqrt{2C-4\eta-p^2-x^2}\right)}{2\sqrt{2C-4\eta-p^2-x^2}}\delta\left(\frac{1}{2}(p^2+x^2){\rm e}^{2\eta}-K\right)\\
&=\int{\rm d}x\int{\rm d}p\int{\rm d}\eta\frac{\exp(\eta)}{\sqrt{2C-4\eta-p^2-x^2}}\delta\left(\frac{1}{2}(p^2+x^2){\rm e}^{2\eta}-K\right)\\
&=\int{\rm d}x\int{\rm d}p\int{\rm d}\eta\frac{\delta\left(\frac{1}{2}(p^2+x^2)\eta^2-K\right)}{\sqrt{2C-4\ln\eta-p^2-x^2}}\\
&=\int{\rm d}x\int{\rm d}p\int{\rm d}\eta\frac{1}{\sqrt{2C-4\ln\eta-p^2-x^2}}\frac{\delta\left(\eta-\sqrt{\frac{2K}{p^2+x^2}}\right)+\delta\left(\eta+\sqrt{\frac{2K}{p^2+x^2}}\right)}{2\sqrt{\frac{2K}{p^2+x^2}}}\\
&=\frac{1}{\sqrt{2K}}\int{\rm d}x\int{\rm d}p\sqrt{\frac{\mathcal{H}(x,p)}{C-\ln\left\{\frac{K}{\mathcal{H}(x,p)}\right\}-\mathcal{H}(x,p)}}\\
\therefore f(H)&\propto\sqrt{\frac{\mathcal{H}(x,p)}{C-\ln\left\{\frac{K}{\mathcal{H}(x,p)}\right\}-\mathcal{H}(x,p)}}
\end{align*}
$$
c.
$$
\begin{align*}
C-\ln\left\{\frac{K}{\mathcal{H}(x,p)}\right\}-\mathcal{H}(x,p)&\leq 0\\
\therefore \ln\left\{\frac{\mathcal{H}(x,p)}{K}\right\}\leq \frac{\mathcal{H}(x,p)}{K}-\frac{C}{K}
\end{align*}
$$
を満たす領域には解が存在しない。
Problem 4.5
N粒子系の相互作用が以下の2体ポテンシャルで表現される場合を考える。
$$
\begin{align*}
U(\mathbf{r},\cdots,\mathbf{r}_N)&=\sum_{i=1}^N\sum_{j>i}^Nu(|\mathbf{r}_i-\mathbf{r}_j|)
\end{align*}
$$
希薄密度の極限においては,各粒子はそれ以外の1粒子とのみ相互作用すると仮定することができる。
a. 希薄密度の極限においてカノニカル分布が以下の式で表現できることを示せ。
$$
\begin{align*}
Q(N,V,T)&=\frac{(N-1)!!V^{N/2}}{N!\lambda^{3N}}\left[4\pi\int_0^{\infty}{\rm d}r r^2{\rm e}^{-\beta u(r)}\right]^{N/2}
\end{align*}
$$
b. 同極限において動径分布関数$${g(r)}$$が$${\exp[-\beta u(r)]}$$に比例することを示せ。
c. 同極限において第二ビリアル係数が
$$
\begin{align*}
B_2(T)&=-2\pi\int_{0}^{\infty}{\rm d}rr^2f(r)
\end{align*}
$$
となることを示せ。ここで,$${f(r)={\rm e}^{-\beta u(r)}-1}$$である。
a. N個の粒子を$${N/2}$$個の2粒子のペアに分ける組み合わせは$${(N-1)!!}$$通り存在する。
また,2粒子系に対する分配関数は
$$
\begin{align*}
\int_{D(V)}{\rm d}\mathbf{r}_1\int_{D(V)}{\rm d}\mathbf{r}_2\exp\left(-\beta u(|\mathbf{r}_1-\mathbf{r}_2|)\right)&=\int_{D(V)}{\rm d}\mathbf{R}\int_{D(V)}{\rm d}\mathbf{r}\exp\left(-\beta u(r)\right)\\
&=V\int_{D(V)}{\rm d}\mathbf{r}\exp\left(-\beta u(r)\right)\\
&\simeq 4 \pi V\int_{0}^{\infty}{\rm d}r\exp\left(-\beta u(r)\right)\\
\end{align*}
$$
と計算される。
$$
\begin{align*}
\therefore Q(N,V,T)&=\frac{(N-1)!!V^{N/2}}{N!\lambda^{3N}}\left[4\pi\int_0^{\infty}{\rm d}r r^2{\rm e}^{-\beta u(r)}\right]^{N/2}
\end{align*}
$$
b.
$$
\begin{align*}
g^{(2)}(\mathbf{r}_1,\mathbf{r}_2)&\propto\int_{D(V)}{\rm d}\mathbf{r}_3\cdots\mathbf{r}_N\exp\left(-\beta\sum_{i=1}^N\sum_{j>i}^Nu(|\mathbf{r}_i-\mathbf{r}_j|)\right)\\
&=\exp\left(-\beta u(|\mathbf{r}_1-\mathbf{r}_2|)\right)\int_{D(V)}{\rm d}\mathbf{r}_3\cdots\mathbf{r}_N\exp\left(-\beta\sum_{i=2}^N\sum_{j>i}^Nu(|\mathbf{r}_i-\mathbf{r}_j|)\right)\\
&\propto \exp\left(-\beta u(|\mathbf{r}_1-\mathbf{r}_2|)\right)\\
\therefore g(r)&\propto \exp\left(-\beta u(r)\right)
\end{align*}
$$
c. 式(4.6.74)
$$
\begin{align*}
B_2(T)&\simeq -\frac{2\pi}{3k_{\rm B}T}\int_0^{\infty}{\rm d}r r^3u'(r)g(r)
\end{align*}\tag{4.6.74}
$$
に$${g(r)={\rm e}^{-\beta u(r)}}$$を代入すると,
$$
\begin{align*}
B_2(T)&= -\frac{2\pi}{3k_{\rm B}T}\int_0^{\infty}{\rm d}r r^3u'(r){\rm e}^{-\beta u(r)}\\
&=-\frac{2\pi}{3k_{\rm B}T}\left\{\left[-r^3{\rm e}^{-\beta u(r)}/\beta\right]_0^{\infty}+\frac{3}{\beta}\int_0^{\infty}{\rm d}r r^2{\rm e}^{-\beta u(r)}\right\}\\
&=-2\pi\int_0^{\infty}{\rm d}r r^2{\rm e}^{-\beta u(r)}
\end{align*}
$$
となる。$${f(r)={\rm e}^{-\beta u(r)}-1}$$とすると積分が発散してしまうため,誤植の可能性がある。
Problem 4.6
質量$${m}$$の$${N}$$粒子からなる温度$${T}$$の理想気体が半径$${a}$$,高さ$${L}$$の円筒形の容器に格納されているとする。容器は円筒の軸方向($${z}$$軸とする)に各速度$${\omega}$$で回転している。さらに,気体は重力定数$${g}$$の重力下に置かれている。それゆえ,気体のハミルトニアンは
$$
\begin{align*}
\mathcal{H}&=\sum_{i=1}^Nh(\mathbf{r}_i,\mathbf{p}_i)
\end{align*}
$$
となる。ここで,$${h(\mathbf{r}_i,\mathbf{p}_i)}$$は単粒子のハミルトニアンであり,
$$
\begin{align*}
h(\mathbf{r}_i,\mathbf{p}_i)&=\frac{\mathbf{p}_i^2}{2m}-\omega(\mathbf{r}_i\times\mathbf{p}_i)_z+mgz_i
\end{align*}
$$
である。ここで,$${(\mathbf{r}\times\mathbf{p})_z}$$は$${\mathbf{r}\times\mathbf{p}}$$の$${z}$$軸成分である。
a. 今回のようにハミルトニアンが分離できる場合,カノニカル分配関数$${Q(N,V,T)}$$は以下のように表現できることを示せ。
$$
\begin{align*}
Q(N,V,T)&=\frac{1}{N!}[q(V,T)]^N
\end{align*}
$$
ここで,
$$
\begin{align*}
q(V,T)&=\frac{1}{h^3}\int{\rm d}\mathbf{p}\int_{D(V)}{\rm d}\mathbf{r}{\rm e}^{-\beta h(\mathbf{r},\mathbf{p})}
\end{align*}
$$
である。
b. 一般的に化学ポテンシャル$${\mu(N,V,T)}$$は
$$
\begin{align*}
\mu(N,V,T)&=k_{\rm B}T\ln\left[\frac{Q(N-1,V,T)}{Q(N,V,T)}\right]
\end{align*}
$$
で与えられることを示せ。ここで,$${Q(N-1,V,T)}$$は$${N-1}$$粒子系の分配関数である。
c. この理想気体の分配関数を計算せよ。
d. この理想気体のヘルムホルツ自由エネルギーを計算せよ。
e. この理想気体の全内部エネルギーを計算せよ。
f. この理想気体の熱容量を計算せよ。
g. この理想気体の状態方程式は?
a.
$$
\begin{align*}
Q(N,V,T)&=\frac{1}{h^{3N}N!}\int{\rm d}^N\mathbf{r}\int{\rm d}^N\mathbf{p}\exp\left(-\beta\mathcal{H}(\mathbf{r},\mathbf{p})\right)\\
&=\frac{1}{h^{3N}N!}\int{\rm d}^N\mathbf{r}\int{\rm d}^N\mathbf{p}\exp\left(-\beta\sum_{i=1}^Nh(\mathbf{r}_i,\mathbf{p}_i)\right)\\
&=\frac{1}{h^{3N}N!}\int{\rm d}^N\mathbf{r}\int{\rm d}^N\mathbf{p}\prod_{i=1}^N\exp\left(-\beta h(\mathbf{r}_i,\mathbf{p}_i)\right)\\
&=\frac{1}{N!}\prod_{i=1}^N\left[\frac{1}{h^{N}}\int_{D(V)}{\rm d}\mathbf{r}_i\int{\rm d}\mathbf{p}_i\exp\left(-\beta h(\mathbf{r}_i,\mathbf{p}_i)\right)\right]\\
&=\frac{1}{N!}\left[\frac{1}{h^{3}}\int_{D(V)}{\rm d}\mathbf{r}\int{\rm d}\mathbf{p}\exp\left(-\beta h(\mathbf{r},\mathbf{p})\right)\right]^N\\
&=\frac{1}{N!}[q(V,T)]^N
\end{align*}
$$
b. ヘルムホルツ自由エネルギーを$${A(N,V,T)}$$とおくと,
$$
\begin{align*}
\mu(N,V,T)&=\left(\frac{\partial A(N,V,T)}{\partial N}\right)_{V,T}\\
&\simeq \frac{A(N,V,T)-A(N-1,V,T)}{1}\\
&=-k_{\rm B}T\ln Q(N,V,T)+k_{\rm B}T\ln Q(N-1,V,T)\\
&=k_{\rm B}T\ln\left[\frac{Q(N-1,V,T)}{Q(N,V,T)}\right]
\end{align*}
$$
c.
$$
\begin{align*}
h(\mathbf{r},\mathbf{p})&=\frac{\mathbf{p}^2}{2m}-\omega(\mathbf{r}\times\mathbf{p})_z+mgz\\
&=\frac{1}{2m}\left\{(p_x+m\omega y)^2+(p_y-m\omega x)^2+p_z^2\right\}-\frac{m\omega^2}{2}\left(x^2+y^2\right)+mgz
\end{align*}
$$
より,
$$
\begin{align*}
q(V,T)&=\frac{1}{h^{3}}\int_{D(V)}{\rm d}\mathbf{r}\int{\rm d}\mathbf{p}\exp\left(-\beta h(\mathbf{r},\mathbf{p})\right)\\
&=\frac{1}{h^{3}}\int_{D(V)}{\rm d}\mathbf{r}\int{\rm d}\mathbf{p}\exp\left[-\beta \left(\frac{1}{2m}\left\{(p_x+m\omega y)^2+(p_y-m\omega x)^2+p_z^2\right\}-\frac{m\omega^2}{2}\left(x^2+y^2\right)+mgz\right)\right]\\
&=\frac{2\pi}{h^{3}}\int_{0}^a{\rm d}rr\exp\left(\frac{\beta m\omega^2 r^2}{2}\right)\int_{0}^L{\rm d}z\exp\left(-\beta mgz\right)\int_{-\infty}^{\infty}{\rm d}p_x\exp\left(-\frac{\beta}{2m}(p_x+m\omega y)^2\right)\int_{-\infty}^{\infty}{\rm d}p_y\exp\left(-\frac{\beta}{2m}(p_y-m\omega x)^2\right)\int_{-\infty}^{\infty}{\rm d}p_z\exp\left(-\frac{\beta}{2m}p_z^2\right)\\
&=\frac{2\pi}{h^{3}}\cdot\frac{\exp\left(\frac{\beta m \omega^2a^2}{2}\right)-1}{\beta m\omega^2}\cdot\frac{1-\exp(-\beta mgL)}{\beta mg}\cdot\left(\frac{2m\pi}{\beta}\right)^{3/2}\\
&=\frac{(2\pi)^{5/2}}{h^{3}\beta^{7/2}m^{1/2}\omega^2g}\left(\exp\left(\frac{\beta m \omega^2a^2}{2}\right)-1\right)\left(1-\exp(-\beta mgL)\right)
\end{align*}
$$
$$
\begin{align*}
\therefore Q(N,V,T)&=\frac{1}{N!}[q(V,T)]^N\\
&=\frac{1}{N!}\left[\frac{(2\pi)^{5/2}}{h^{3}\beta^{7/2}m^{1/2}\omega^2g}\left(\exp\left(\frac{\beta m \omega^2a^2}{2}\right)-1\right)\left(1-\exp(-\beta mgL)\right)\right]^N\\
\end{align*}
$$
d.
$$
\begin{align*}
A(N,V,T)&=-\frac{1}{\beta}\ln Q(N,V,T)\\
&=-\frac{1}{\beta}\left[-\ln N!+N\ln\left\{\frac{(2\pi)^{5/2}}{h^{3}\beta^{7/2}m^{1/2}\omega^2g}\left(\exp\left(\frac{\beta m \omega^2a^2}{2}\right)-1\right)\left(1-\exp(-\beta mgL)\right)\right\}\right]\\
&\simeq-\frac{N}{\beta}\left[\left\{1+\frac{5}{2}\ln(2\pi)-\ln\left(h^3\beta^{7/2}m^{1/2}\omega^2g\right)+\ln\left(\exp\left(\frac{\beta m \omega^2a^2}{2}\right)-1\right)+\ln\left(1-\exp(-\beta mgL)\right)\right\}-\ln N\right]\\
\end{align*}
$$
e.内部エネルギーを$${U}$$,エントロピーを$${S}$$とすると,
$$
\begin{align*}
U&=A(N,V,T)+TS\\
&=A(N,V,T)-T\left(\frac{\partial A(N,V,T)}{\partial T}\right)_{N,V}\\
&=A(N,V,T)+\beta\left(\frac{\partial A(N,V,T)}{\partial \beta}\right)_{N,V}\\
&=\left(\frac{\partial \beta A(N,V,T)}{\partial \beta}\right)_{N,V}\\
&=N\left[\frac{7}{2\beta}-\frac{m\omega^2a^2}{2}\frac{1}{1-{\rm e}^{-\beta m\omega^2a^2/2}}-\frac{mgL}{{\rm e}^{\beta mgL}-1}\right]
\end{align*}
$$
f. 熱容量を$${C}$$とすると,
$$
\begin{align*}
C&=\frac{\partial U}{\partial T}\\
&=-k_{\rm B}\beta^2\frac{\partial U}{\partial \beta}\\
&=Nk_{\rm B}\left[\frac{7}{2}-\left(\frac{\beta m\omega^2a^2}{2}\right)^2\frac{{\rm e}^{-\beta m\omega^2a^2/2}}{(1-{\rm e}^{-\beta m\omega^2a^2/2})^2}-\frac{(\beta mgL)^2{\rm e}^{\beta mgL}}{({\rm e}^{\beta mgL}-1)^2}\right]\\
\end{align*}
$$
g. $${V=\pi a^2\times L}$$であることを考慮すると,圧力$${p}$$は
$$
\begin{align*}
p&=-\left(\frac{\partial A(N,V,T)}{\partial V}\right)_{N,T}\\
&=-\frac{1}{2\pi aL}\left(\frac{\partial A(N,V,T)}{\partial a}\right)_{N,T}-\frac{1}{\pi a^2}\left(\frac{\partial A(N,V,T)}{\partial L}\right)_{N,T}\\
&=\frac{Nm}{\pi}\left(\frac{\omega^2}{2L}\frac{1}{1-{\rm e}^{-\beta m\omega^2a^2/2}}+\frac{g}{a^2}\frac{1}{{\rm e}^{\beta mgL}-1}\right)
\end{align*}
$$
Problem 4.7
相互作用しないN個の2原子分子が一辺の長さが$${L}$$の立方体(体積$${V=L^3}$$)に閉じ込められた古典系が温度$${T}$$に保たれているとする。単分子のハミルトニアンは
$$
\begin{align*}
h(\mathbf{r}_1,\mathbf{r}_2,\mathbf{p}_1,\mathbf{p}_2)&=\frac{\mathbf{p}_1^2}{2m_1}+\frac{\mathbf{p}_2^2}{2m_2}+\epsilon|r_{12}-r_0|
\end{align*}
$$
で与えられるとする。ここで,$${r_{12}=|\mathbf{r}_1-\mathbf{r}_2|}$$は2原子分子間の原子間距離である。
a. カノニカル分配関数を計算せよ。
b. ヘルムホルツ自由エネルギーを計算せよ。
c. 全内部エネルギーを計算せよ。
d. 熱容量を計算せよ。
e. 分子の結合長の自乗平均$${\langle|\mathbf{r}_1-\mathbf{r}_2|^2\rangle}$$を計算せよ。
a. $${\mathbf{R}:=\frac{m_1\mathbf{r}_1+m_2\mathbf{r}_2}{m_1+m_2}, \mathbf{r}:=\mathbf{r}_1-\mathbf{r}_2}$$とおくと正準共役な運動量$${\mathbf{P},\mathbf{p}}$$は
$$
\begin{align*}
\mathbf{P}&=(m_1+m_2)\dot{\mathbf{R}}\\
&=:M\dot{\mathbf{R}}\\
\mathbf{p}&=\frac{m_1m_2}{(m_1+m_2)}\dot{\mathbf{r}}\\
&=:\mu\dot{\mathbf{r}}\\
\end{align*}
$$
となり,また1分子あたりのハミルトニアン$${h(\mathbf{R},\mathbf{r},\mathbf{P},\mathbf{p})}$$は
$$
\begin{align*}
h(\mathbf{R},\mathbf{r},\mathbf{P},\mathbf{p})&=\frac{\mathbf{P}^2}{2M}+\frac{\mathbf{p}^2}{2\mu}+\epsilon|r-r_0|
\end{align*}
$$
となる。
これを用いて1分子あたりの分配関数を計算すると,
$$
\begin{align*}
q(V,T)&=\frac{1}{h^6}\int_{D(V)}{\rm d}\mathbf{R}\int_{D(V)}{\rm d}\mathbf{r}\int{\rm d}\mathbf{P}\int{\rm d}\mathbf{p}\exp\left(-\beta h(\mathbf{R},\mathbf{r},\mathbf{P},\mathbf{p})\right)\\
&=\frac{1}{h^6}\int_{D(V)}{\rm d}\mathbf{R}\int_{D(V)}{\rm d}\mathbf{r}\exp\left(-\beta\epsilon|r-r_0|\right)\int{\rm d}\mathbf{P}\exp\left(- \frac{\beta\mathbf{P}^2}{2M}\right)\int{\rm d}\mathbf{p}\exp\left(- \frac{\beta\mathbf{p}^2}{2\mu}\right)\\
&=\frac{V(M\mu)^{3/2}}{h^6}\left(\frac{2\pi}{\beta}\right)^3\int_{D(V)}{\rm d}\mathbf{r}\exp\left(-\beta\epsilon|r-r_0|\right)\\
&\simeq\frac{4\pi V(M\mu)^{3/2}}{h^6}\left(\frac{2\pi}{\beta}\right)^3\left\{\int_0^{r_0}{\rm d}rr^2\exp\left(\beta\epsilon(r-r_0)\right)+\int_{r_0}^{\infty}{\rm d}rr^2\exp\left(-\beta\epsilon(r-r_0)\right)\right\}\\
&=\frac{8\pi V(M\mu)^{3/2}}{h^6}\left(\frac{2\pi}{\beta}\right)^3\left\{\frac{r_0^2}{\beta\epsilon}+\frac{1}{\beta^3\epsilon^3}\left(2-{\rm e}^{-\beta\epsilon r_0}\right)\right\}\\
\end{align*}
$$
$$
\begin{align*}
\therefore Q(N,V,T)&=\frac{1}{N!}[q(V,T)]^N\\
&=\frac{1}{N!}\left[\frac{8\pi V(M\mu)^{3/2}}{h^6}\left(\frac{2\pi}{\beta}\right)^3\left\{\frac{r_0^2}{\beta\epsilon}+\frac{1}{\beta^3\epsilon^3}\left(2-{\rm e}^{-\beta\epsilon r_0}\right)\right\}\right]^N
\end{align*}
$$
b.
$$
\begin{align*}
A(N,V,T)&=-\frac{1}{\beta}\ln Q(N,V,T)\\
&=-\frac{1}{\beta}\left(-\ln N!+N\ln\left[\frac{8\pi V(M\mu)^{3/2}}{h^6}\left(\frac{2\pi}{\beta}\right)^3\left\{\frac{r_0^2}{\beta\epsilon}+\frac{1}{\beta^3\epsilon^3}\left(2-{\rm e}^{-\beta\epsilon r_0}\right)\right\}\right]\right)\\
&\simeq\frac{1}{\beta}\left(N\ln N-N-N\ln\left[\frac{8\pi V(M\mu)^{3/2}}{h^6}\left(\frac{2\pi}{\beta}\right)^3\left\{\frac{r_0^2}{\beta\epsilon}+\frac{1}{\beta^3\epsilon^3}\left(2-{\rm e}^{-\beta\epsilon r_0}\right)\right\}\right]\right)\\
\end{align*}
$$
c.
$$
\begin{align*}
U&=\left(\frac{\partial \beta A(N,V,T)}{\partial \beta}\right)_{N,V}\\
&=\frac{N}{\beta}\left[\frac{12+4(\beta\epsilon r_0)^2-(6+\beta\epsilon r_0){\rm e}^{-\beta\epsilon r_0}}{2+(\beta\epsilon r_0)^2-{\rm e}^{-\beta\epsilon r_0}}\right]
\end{align*}
$$
d.
$$
\begin{align*}
C&=-k_{\rm B}\beta^2\frac{\partial U}{\partial \beta}\\
&=-k_{\rm B}\beta^2\epsilon r_0\frac{\partial U}{\partial \beta\epsilon r_0}\\
&=-Nk_{\rm B}(\epsilon r_0\beta)^2\frac{\partial }{\partial \beta\epsilon r_0}\left[\frac{1}{\beta\epsilon r_0}\frac{12+4(\beta\epsilon r_0)^2-(6+\beta\epsilon r_0){\rm e}^{-\beta\epsilon r_0}}{2+(\beta\epsilon r_0)^2-{\rm e}^{-\beta\epsilon r_0}}\right]\\
&=Nk_{\rm B}\frac{-6{\rm e}^{-2\beta\epsilon r_0}+(\beta\epsilon r_0)\left\{-(\beta\epsilon r_0)^3+12(\beta\epsilon r_0)^2+20(\beta\epsilon r_0)+24\right\}{\rm e}^{-\beta\epsilon r_0}-4\left\{(\beta\epsilon r_0)^2+1\right\}\left\{(\beta\epsilon r_0)^2+6\right\}}{\left\{2+(\beta\epsilon r_0)^2-{\rm e}^{-\beta\epsilon r_0}\right\}^2}
\end{align*}
$$
e.
$$
\begin{align*}
\langle|\mathbf{r}_1-\mathbf{r}_2|^2\rangle&=\frac{\int_{D(V)}{\rm d}\mathbf{r}r^2{\rm e}^{-\beta\epsilon|r-r_0|}}{\int_{D(V)}{\rm d}\mathbf{r}{\rm e}^{-\beta\epsilon|r-r_0|}}\\
&=\frac{\frac{2r_o^4}{\beta\epsilon}+\frac{24r_o^2}{\beta^3\epsilon^3}+\frac{24}{\beta^5\epsilon^5}\left(2-{\rm e}^{-\beta\epsilon r_0}\right)}{\frac{r_0^2}{\beta\epsilon}+\frac{1}{\beta^3\epsilon^3}\left(2-{\rm e}^{-\beta\epsilon r_0}\right)}
\end{align*}
$$
Problem 4.8
4.11節の積分方法を用いて,質量$${m=1}$$,振動数$${\omega=1}$$,温度$${k_{\rm B}T=1}$$の場合のNose-Hoover chain方程式を積分するプログラムを書け。以下の解析解と比較することにより,数値計算によって正しい運動量と位置の分布が得られることを実証せよ。
$$
\begin{align*}
f(p)&=\frac{1}{\sqrt{2\pi mk_{\rm B}T}}{\rm e}^{-\frac{p^2}{2mk_{\rm B}T}}\\
f(x)&=\sqrt{\frac{m\omega^2}{2\pi k_{\rm B}T}}{\rm e}^{-\frac{m\omega^2x^2}{2k_{\rm B}T}}
\end{align*}
$$
Liouville演算子は以下の通りである。
$$
\begin{align*}
{\rm i}\mathcal{L}_1&=p\frac{\partial }{\partial x}\\
{\rm i}\mathcal{L}_2&=-x\frac{\partial }{\partial p}\\
{\rm i}\mathcal{L}_{\rm NHC}&=-\frac{p_{\eta_1}}{Q}p\frac{\partial }{\partial p}+\sum_{j=1}^M\frac{p_{\eta_j}}{Q}\frac{\partial }{\partial \eta_j}+\sum_{j=1}^{M-1}\left\{G_j -p_{\eta_j}\frac{p_{\eta_{j+1}}}{Q}\right\}\frac{\partial }{\partial p_{\eta_j}}+G_M\frac{\partial }{\partial p_{\eta_M}}\\
G_1&=p^2-1\\
G_j&=\frac{p_{\eta_{j-1}}^2}{Q}-1\ \ \ (j\geq 2)\\
\end{align*}
$$
参考文献2を参考にしてpythonで実装した例を以下に示す。
# Import libraries
from fractions import Fraction
import numpy as np
import itertools
import matplotlib.pyplot as plt
### Input parameters ###
N_c = 4 # The number of decompotiosion for the operator exp(i * L_NHC * dt / 2)
dt = 0.05 # time step
n_steps = 50000 # The number of iteration
M = 2 # The number of chains
Q = 1 # The time scale parameter for all chains
# Seven weights of the Yodhida scheme for a sixth-order scheme
N_sy = 7
w = [0] * N_sy
w[0] = w[6] = 0.784513610477560
w[1] = w[5] = 0.235573213359357
w[2] = w[4] = -1.17767998417887
w[3] = 1 - 2 * np.sum(w[:3])
# Initial values of dynamical variables
x = [0.0]
p = [np.random.normal(0, 1)]
eta = np.zeros(M)
p_eta = np.random.normal(0, 1, M)
# Define functions
def updateDynamicalVariables(p_now, eta, p_eta):
for n_c, n_sy in itertools.product(range(N_c), range(N_sy)):
scale = 1.0
KE = p_now ** 2
delta_j = w[n_sy] * dt / N_c
p_eta[M - 1] += 0.25 * delta_j * (p_eta[M - 2] ** 2 / Q - 1)
for m in range(M - 2, -1, -1):
p_eta[m] *= np.exp(-0.125 * delta_j * p_eta[m + 1])
if m == 0:
p_eta[m] += 0.25 * delta_j * (KE - 1)
else:
p_eta[m] += 0.25 * delta_j * (p_eta[m - 1] ** 2 / Q - 1)
p_eta[m] *= np.exp(-0.125 * delta_j * p_eta[m + 1])
scale *= np.exp(-0.5 * delta_j * p_eta[0] / Q)
KE *= np.exp(-1.0 * delta_j * p_eta[0] / Q)
for m in range(M):
eta[m] += 0.5 * delta_j * p_eta[m]
for m in range(0, M - 1, 1):
p_eta[m] *= np.exp(-0.125 * delta_j * p_eta[m + 1])
if m == 0:
p_eta[m] += 0.25 * delta_j * (KE - 1)
else:
p_eta[m] += 0.25 * delta_j * (p_eta[m - 1] ** 2 / Q - 1)
p_eta[m] *= np.exp(-0.125 * delta_j * p_eta[m + 1])
p_eta[M - 1] += 0.25 * delta_j * (p_eta[M - 2] ** 2 / Q - 1)
p_now *= scale
return p_now, eta, p_eta
def conservedEnergy(x, p, eta, p_eta):
return 0.5 * p ** 2 + 0.5 * x ** 2 + 0.5 * np.sum(np.array(p_eta) ** 2) / Q + np.sum(eta)
###---- The below is the code ----###
# The numerical integration
x_now = x[-1]
p_now = p[-1]
H0 = conservedEnergy(x_now, p_now, eta, p_eta)
dH = 0.0
for n_step in range(1, n_steps + 1):
p_now, eta, p_eta = updateDynamicalVariables(p_now, eta, p_eta)
p_now -= 0.5 * dt * x_now
x_now += dt * p_now
p_now -= 0.5 * dt * x_now
p_now, eta, p_eta = updateDynamicalVariables(p_now, eta, p_eta)
x.append(x_now)
p.append(p_now)
H = conservedEnergy(x_now, p_now, eta, p_eta)
dH += abs(H / H0 - 1)
if n_step % 500 == 0:
err_H = dH / n_step
print(n_step, err_H)
# Export time history of physical dynamical variables to csv file
result = np.array([range(n_steps + 1), x, p]).T
header = 'n_step, x, p'
with open('time_history.csv', 'wb') as f:
np.savetxt(f, result, delimiter = ",", header = header, fmt = "%.5e")
# Plot frequencies and compare the analytical result
x_range = np.linspace(np.min(x) - 1, np.max(x) + 1, 101)
x_ana = np.exp(-0.5 * x_range ** 2) / np.sqrt(2 * np.pi)
plt.plot(x_range, x_ana, label = 'analytical')
plt.hist(x, bins = 41, density = True, label = 'numerical')
plt.legend()
plt.xlabel('x')
plt.ylabel('density')
plt.savefig('x.png')
plt.figure()
p_range = np.linspace(np.min(p) - 1, np.max(p) + 1, 101)
p_ana = np.exp(-0.5 * p_range ** 2) / np.sqrt(2 * np.pi)
plt.plot(p_range, p_ana, label = 'analytical')
plt.hist(p, bins = 41, density = True, label = 'numerical')
plt.legend()
plt.xlabel('p')
plt.ylabel('density')
plt.savefig('p.png')
plt.figure()


Problem 4.9
以下の単一のホロノミック拘束条件が課せられたN粒子系を考える。
$$
\begin{align*}
\sigma(\mathbf{r}_1,\cdots,\mathbf{r}_N)&:=\sigma(\mathbf{r})&=0
\end{align*}
$$
ガウスの最小束縛原理を用いると,運動方程式は以下のようになることを思い出そう。
$$
\begin{align*}
\dot{\mathbf{r}}_i&=\frac{\mathbf{p}_i}{m_i}\\
\dot{\mathbf{p}}_i&=\mathbf{F}_i-\left[\frac{\sum_j\mathbf{F}_j\cdot\nabla_j\sigma/m_j+\sum_{j,k}\nabla_j\nabla_k\sigma\cdot\cdot\mathbf{p}_j\mathbf{p}_k/(m_jm_k)}{\sum_j(\nabla_j\sigma)^2/m_j}\right]\nabla_i\sigma
\end{align*}
$$
節4.9の手法を利用することにより,これらの運動方程式が以下の分配関数を生成することを示せ。
$$
\begin{align*}
\Omega&=\int{\rm d}^N\mathbf{p}{\rm d}^N\mathbf{r}Z(\mathbf{r})\delta\left(\mathcal{H}(\mathbf{r},\mathbf{p})-E\right)\delta\left(\sigma(\mathbf{r})\right)\delta\left(\dot{\sigma}(\mathbf{r},\mathbf{p})\right)
\end{align*}
$$
ここで,
$$
\begin{align*}
Z(\mathbf{r})&=\sum_{i=1}^N\frac{1}{m_i}\left(\frac{\partial \sigma}{\partial \mathbf{r}_i}\right)^2
\end{align*}
$$
である。
この結果は,1983年にRyckaertとCiccottiによってはじめて導かれた。
$$
\begin{align*}
\dot{\sigma}&=\sum_i\nabla_i\sigma\cdot\mathbf{p}_i/m_i
\end{align*}
$$
であることに注意して$${\dot{\mathbf{p}}_i}$$を$${\mathbf{p}_i}$$で微分すると,
$$
\begin{align*}
\frac{\partial \dot{\mathbf{p}}_i}{\partial \mathbf{p}_i}&=-\frac{\nabla_i\sigma}{\sum_j(\nabla_j\sigma)^2/m_j}\cdot\frac{\partial }{\partial \mathbf{p}_i}\left\{\sum_{j,k}\nabla_j\nabla_k\sigma\cdot\cdot\mathbf{p}_j\mathbf{p}_k/(m_jm_k)\right\}\\
&=-\frac{\nabla_i\sigma}{\sum_j(\nabla_j\sigma)^2/m_j}\cdot\frac{\partial }{\partial \mathbf{p}_i}\left\{\sum_{j}\nabla_j\dot{\sigma}\cdot\frac{\mathbf{p}_j}{m_j}\right\}\\
&=-\frac{\nabla_i\sigma}{\sum_j(\nabla_j\sigma)^2/m_j}\cdot\sum_{j}\left\{\nabla_j\dot{\sigma}\left(\frac{\partial }{\partial \mathbf{p}_i}\cdot\frac{\mathbf{p}_j}{m_j}\right)+\frac{\mathbf{p}_j}{m_j}\left(\frac{\partial }{\partial \mathbf{p}_i}\cdot\nabla_j\dot{\sigma}\right)\right\}\\
&=-\frac{\nabla_i\sigma}{\sum_j(\nabla_j\sigma)^2/m_j}\cdot\sum_{j}\left\{\nabla_j\dot{\sigma}\frac{\delta_{ij}}{m_j}+\frac{\mathbf{p}_j}{m_j}\nabla_j\sum_k\nabla_k\sigma\frac{\delta_{ik}}{m_k}\right\}\\
&=-\frac{\nabla_i\sigma}{\sum_j(\nabla_j\sigma)^2/m_j}\cdot\left\{\frac{\nabla_i\dot{\sigma}}{m_i}+\sum_{j}\frac{\mathbf{p}_j}{m_j}\nabla_j\frac{\nabla_i\sigma}{m_i}\right\}\\
&=-\frac{\nabla_i\sigma}{\sum_j(\nabla_j\sigma)^2/m_j}\cdot\left\{\frac{\nabla_i\dot{\sigma}}{m_i}+\nabla_i\sum_{j}\frac{\mathbf{p}_j}{m_j}\frac{\nabla_j\sigma}{m_i}\right\}\\
&=-\frac{\nabla_i\sigma}{\sum_j(\nabla_j\sigma)^2/m_j}\cdot\left\{\frac{\nabla_i\dot{\sigma}}{m_i}+\frac{1}{m_i}\nabla_i\sum_{j}\frac{\mathbf{p}_j}{m_j}\nabla_j\sigma\right\}\\
&=-\frac{\nabla_i\sigma}{\sum_j(\nabla_j\sigma)^2/m_j}\cdot\frac{2\nabla_i\dot{\sigma}}{m_i}\\
\end{align*}
$$
となるため,
$$
\begin{align*}
\nabla_{\mathbf{x}}\cdot\dot{\mathbf{x}}&=\sum_{i=1}^N\frac{\partial \dot{\mathbf{p}}_i}{\partial \mathbf{p}_i}\\
&=-\frac{2\sum_{i=1}^N\nabla_i\dot{\sigma}\cdot\nabla_i\sigma/m_i}{\sum_j(\nabla_j\sigma)^2/m_j}\\
&=-\frac{{\rm d}}{{\rm d}t}\ln\left\{\sum_{i=1}^N\frac{1}{m_i}(\nabla_i\sigma)^2\right\}\\
&=-\frac{{\rm d}}{{\rm d}t}\ln\left\{Z(\mathbf{r})\right\}\\
&=\dot{w}
\end{align*}
$$
$$
\begin{align*}
\therefore \sqrt{g}&=\exp(-w)\\
&=Z(\mathbf{r})
\end{align*}
$$
以上より,微小体積要素$${{\rm d}^N\mathbf{p}{\rm d}^N\mathbf{r}Z(\mathbf{r})}$$が保存すること,及び3つの保存量が存在することを考慮すると分配関数は
$$
\begin{align*}
\Omega&=\int{\rm d}^N\mathbf{p}{\rm d}^N\mathbf{r}Z(\mathbf{r})\delta\left(\mathcal{H}(\mathbf{r},\mathbf{p})-E\right)\delta\left(\sigma(\mathbf{r})\right)\delta\left(\dot{\sigma}(\mathbf{r},\mathbf{p})\right)
\end{align*}
$$
で与えられる。
Problem 4.10
カノニカルアンサンブルにおける古典ビリアル定理は1918年にRichard C. Tolmanによって導かれた。以下のカノニカル平均
$$
\begin{align*}
\left\langle{\rm x}_i\frac{\partial \mathcal{H}}{\partial {\rm x}_j}\right\rangle&=\frac{1}{N!h^{3N}Q(N,V,T)}\int{\rm d}\mathbf{x}{\rm x}_i\frac{\partial \mathcal{H}}{\partial {\rm x}_j}{\rm e}^{-\beta\mathcal{H}(\mathbf{x})}&=k_{\rm B}T\delta_{ij}
\end{align*}
$$
が成立することを証明せよ。この結果を導く際に必要となる前提条件は何か?
$${{\rm x}_j}$$に関して部分積分すると,
$$
\begin{align*}
\left\langle{\rm x}_i\frac{\partial \mathcal{H}}{\partial {\rm x}_j}\right\rangle&=\frac{1}{N!h^{3N}Q(N,V,T)}\int{\rm d}\mathbf{x}{\rm x}_i\frac{\partial \mathcal{H}}{\partial {\rm x}_j}{\rm e}^{-\beta\mathcal{H}(\mathbf{x})}\\
&=\frac{1}{\beta N!h^{3N}Q(N,V,T)}\left\{-\int{\rm d}\mathbf{x}_{-j}\left[{\rm x}_i{\rm e}^{-\beta\mathcal{H}(\mathbf{x})}\right]_{{\rm x}_j^{\rm min}}^{{\rm x}_j^{\rm max}}+\delta_{ij}\int{\rm d}\mathbf{x}{\rm e}^{-\beta\mathcal{H}(\mathbf{x})}\right\}\\
&=k_{\rm B}T\delta_{ij}-\frac{k_{\rm B}T}{N!h^{3N}Q(N,V,T)}\int{\rm d}\mathbf{x}_{-j}\left[{\rm x}_i{\rm e}^{-\beta\mathcal{H}(\mathbf{x})}\right]_{{\rm x}_j^{\rm min}}^{{\rm x}_j^{\rm max}}
\end{align*}
$$
境界で$${{\rm e}^{-\beta\mathcal{H}(\mathbf{x})}=0}$$,もしくは$${{\rm e}^{-\beta\mathcal{H}(\mathbf{x}^{\rm min})}={\rm e}^{-\beta\mathcal{H}(\mathbf{x}^{\rm max})}}$$(周期境界条件)を仮定することにより,
$$
\begin{align*}
\left\langle{\rm x}_i\frac{\partial \mathcal{H}}{\partial {\rm x}_j}\right\rangle&=k_{\rm B}T\delta_{ij}
\end{align*}
$$
が成立する。
Problem 4.11
1成分の等方的な液体or気体の構造因子$${S(q)}$$が動径分布関数$${g(r)}$$と式(4.6.31)によって関連付けられることを示せ。
$$
\begin{align*}
S(q)&=4\pi\rho\int_{0}^{\infty}{\rm d}rr^2(g(r)-1)\frac{\sin qr}{qr}
\end{align*}\tag{4.6.31}
$$
$$
\begin{align*}
S(q)&=\frac{1}{N}\left\langle\sum_{i,j}\exp\left({\rm i}\mathbf{q}\cdot(\mathbf{r}_i-\mathbf{r}_j)\right)\right\rangle\\
&=1+\frac{1}{N}\left\langle\sum_{i\neq j}\exp\left({\rm i}\mathbf{q}\cdot(\mathbf{r}_i-\mathbf{r}_j)\right)\right\rangle\\
&=1+\frac{1}{N}\left\langle\int{\rm d}\mathbf{r}\int{\rm d}\mathbf{r}'\exp\left({\rm i}\mathbf{q}\cdot(\mathbf{r}-\mathbf{r}')\right)\sum_{i\neq j}\delta(\mathbf{r}-\mathbf{r}_i)\delta(\mathbf{r}'-\mathbf{r}_j))\right\rangle\\
&=1+\frac{1}{N}\int{\rm d}\mathbf{r}\int{\rm d}\mathbf{r}'\exp\left({\rm i}\mathbf{q}\cdot(\mathbf{r}-\mathbf{r}')\right)\left\langle\sum_{i\neq j}\delta(\mathbf{r}-\mathbf{r}_i)\delta(\mathbf{r}'-\mathbf{r}_j))\right\rangle\\
&=1+\frac{1}{N}\int{\rm d}\mathbf{r}\int{\rm d}\mathbf{r}'\exp\left({\rm i}\mathbf{q}\cdot(\mathbf{r}-\mathbf{r}')\right)N(N-1)\left\langle\delta(\mathbf{r}-\mathbf{r}_1)\delta(\mathbf{r}'-\mathbf{r}_2))\right\rangle\\
&=1+\rho V\int{\rm d}\mathbf{r}\int{\rm d}\mathbf{r}'\exp\left({\rm i}\mathbf{q}\cdot(\mathbf{r}-\mathbf{r}')\right)g^{(2)}(\mathbf{r},\mathbf{r'})\\
\end{align*}
$$
ここで,重心座標$${\mathbf{R}=(\mathbf{r}+\mathbf{r}')/2}$$と相対座標$${\mathbf{r}''=\mathbf{r}-\mathbf{r}'}$$を導入し,$${\mathbf{q}}$$の方向を$${z}$$軸とする。
等方的な分布を仮定していることを考慮すると,
$$
\begin{align*}
{\rm r.h.s}&=1+\rho V\int_{D(V)}{\rm d}\mathbf{R}\int{\rm d}\mathbf{r}''\exp\left({\rm i}\mathbf{q}\cdot\mathbf{r}''\right)g(r'')\\
&=1+\rho \int{\rm d}\mathbf{r}\exp\left({\rm i}\mathbf{q}\cdot\mathbf{r}\right)g(r)\\
&=1+\rho \int_{0}^{\infty}{\rm d}rr^2\int_{0}^{\pi}{\rm d}\theta\sin\theta\int_{0}^{2\pi}{\rm d}\phi\exp\left({\rm i}qr\cos\theta\right)g(r)\\
&=1+2\pi\rho \int_{0}^{\infty}{\rm d}rr^2\int_{0}^{\pi}{\rm d}\theta\sin\theta\exp\left({\rm i}qr\cos\theta\right)g(r)\\
&=1+4\pi\rho \int_{0}^{\infty}{\rm d}rr^2g(r)\frac{\sin qr}{qr}\\
\therefore S(q)&=1+4\pi\rho \int_{0}^{\infty}{\rm d}rr^2g(r)\frac{\sin qr}{qr}\\
\end{align*}
$$
本文の式(4.6.31)は誤植??
Problem 4.12
N個の相互作用しない同一分子からなる系を考える。ここの分子は$${n}$$個の原子から構成されており,ある化学結合のパターンで結合している。分子内の原子間結合はポテンシャル$${u(\mathbf{r}_1^{(i)},\cdots,u(\mathbf{r}_n^{(i)}), i=1,\cdots,N}$$で表され,原子間の距離が離れるほど大きくなる性質がある。各分子内の原子は質量$${m_k}$$を有する。ここで,$${k=1,\cdots,n}$$である。
a. ハミルトニアンとカノニカル分配関数を書き下し,分配関数は分子単体の分配関数の積として簡略できることを示せ。
b. 分子単体に対して以下の座標変換
$$
\begin{align*}
\mathbf{s}_1&=\frac{1}{M}\sum_{k=1}^nm_k\mathbf{r}_k\\
\mathbf{s}_k&=\mathbf{r}_k-\frac{1}{m_k'}\sum_{l=1}^{k-1}m_l\mathbf
{r}_l\ \ \ {\rm for}\ k=2,\cdots,n\\
m_k'&:=\sum_{l=1}^{k-1}m_l
\end{align*}
$$
を実施した場合,座標$${\mathbf{s}_1}$$にはどのような意味があるであろうか?
$${u(\mathbf{r}_1,\cdots,\mathbf{r}_n)}$$が分子内の原子ペア間の相対座標にしか依存しない場合,分子単体の分配関数は以下の形式となることを示せ。
$$
\begin{align*}
Q(N,V,T)&=\frac{(Vf(n,T))^N}{N!}
\end{align*}
$$
ここで,$${f(n,T)}$$は$${n}$$と$${T}$$のみの関数である。
c. b.の結果を受けて,系の分子の種類によらず,状態方程式は理想気体と同等になることを示せ。
d. 分子単体の分配関数を$${q(n,V,T)=Vf(n,T)}$$と表記する。ここで,異なる種類の分子から構成される系を考える。より具体的に,系には$${A}$$種が$${N_A}$$分子,$${B}$$種が$${N_B}$$分子,$${C}$$種が$${N_C}$$分子,$${D}$$種が$${N_D}$$分子含まれているとする。更に分子間で以下の化学平衡となる化学反応が生じるとする。
$$
\begin{align*}
aA+bB& \rightleftharpoons cC+dD
\end{align*}
$$
想定している状況下ではヘルムホルツ自由エネルギー$${F}$$は$${V,T,N_A, N_B, N_C, N_D}$$の関数となる。化学平衡に達した場合,自由エネルギーは最小($${{\rm d}F=0}$$)となる。
系の体積と温度は一定値に保たれている場合を考える。変数$${\lambda}$$を用いて,$${{\rm d}N_A=a{\rm d}\lambda, {\rm d}N_B=b{\rm d}\lambda, {\rm d}N_C=-c{\rm d}\lambda+{\rm d}N_D=-d{\rm d}\lambda}$$とする。$${\lambda}$$は反応進行度と呼ばれる。
平衡状態において,
$$
\begin{align*}
a\mu_A+b\mu_B-c\mu_C-d\mu_D&=0
\end{align*}\tag{4.14.27}
$$
が成立することを示せ。
ここで,$${\mu_A}$$は$${A}$$種の化学ポテンシャルであり,
$$
\begin{align*}
\mu_A&=-k_{\rm B}T\frac{\ln Q(V,T,N_A,N_B,N_C,N_D)}{\partial N_A}
\end{align*}
$$
で与えられる。$${\mu_B, \mu_C, \mu_D}$$についても同様である。
e. 最終的にに式(4.14.27)は
$$
\begin{align*}
\frac{\rho_C^c\rho_D^d}{\rho_A^a\rho_B^b}&=\frac{(q_C/V)^c(q_D/V)^d}{(q_A/V)^a(q_B/V)^b}
\end{align*}
$$
を意味しており,上式の両辺は温度のみの関数であることを示せ。
ここで,$${q_A, \rho_A}$$はそれぞれ$${A}$$種の分子単体の分配関数,及び数密度である。$${q_B, q_C, q_D}$$や$${\rho_B, \rho_C, \rho_D}$$についても同様である。
右辺の量は通常の平衡定数
$$
\begin{align*}
K&=\frac{P_C^cP_D^d}{P_A^aP_B^b}
\end{align*}
$$
とどのように関連付けられるであろうか?
ここで,$${P_A, P_B, \cdots}$$は各種の分圧である。
a. $${\mathbf{r}_k^{(i)}}$$に正準共役な運動量$${\mathbf{p}_k^{(i)}}$$とおくと,系のハミルトニアン$${\mathcal{H}(\mathbf{r},\mathbf{p})}$$は
$$
\begin{align*}
\mathcal{H}(\mathbf{r},\mathbf{p})&=\sum_{i=1}^N\left\{\sum_{k=1}^n\frac{\left(\mathbf{p}_k^{(i)}\right)^2}{m_k}+u\left(\mathbf{r}_1^{(i)},\cdots,\mathbf{r}_n^{(i)}\right)\right\}
\end{align*}
$$
で与えられる。
対応する分配関数$${Q(N,V,T)}$$は,分子については区別できないことを考慮すると,
$$
\begin{align*}
Q(N,V,T)&=\frac{1}{h^{3nN}N!}\left\{\prod_{i=1}^N\int{\rm d}^n\mathbf{r}^{(i)}\int{\rm d}^n\mathbf{p}^{(i)}\right\}\exp\left(-\beta\sum_{i=1}^N\left\{\sum_{k=1}^n\frac{\left(\mathbf{p}_k^{(i)}\right)^2}{m_k}+u\left(\mathbf{r}_1^{(i)},\cdots,\mathbf{r}_n^{(i)}\right)\right\}\right)\\
&=\frac{1}{N!}\left\{\prod_{i=1}^N\frac{1}{h^{3n}}\int{\rm d}^n\mathbf{r}^{(i)}\int{\rm d}^n\mathbf{p}^{(i)}\exp\left(-\beta\left\{\sum_{k=1}^n\frac{\left(\mathbf{p}_k^{(i)}\right)^2}{m_k}+u\left(\mathbf{r}_1^{(i)},\cdots,\mathbf{r}_n^{(i)}\right)\right\}\right)\right\}\\
&=\frac{1}{N!}\left\{\frac{1}{h^{3n}}\int{\rm d}^n\mathbf{r}\int{\rm d}^n\mathbf{p}\exp\left(-\beta\left\{\sum_{k=1}^n\frac{\mathbf{p}_k^2}{m_k}+u\left(\mathbf{r}_1,\cdots,\mathbf{r}_n\right)\right\}\right)\right\}^{N}\\
&=:\frac{1}{N!}\left\{q(N,V,T)\right\}^{N}\\
\end{align*}
$$
となり,分子単体の分配関数の積として表すことができる。
b. 問題文の座標変換を行ったとすると,原子間の相対距離のみに依存する仮定の下ではポテンシャルエネルギーは重心$${\mathbf{s}_1}$$に依存しない。
$$
\begin{align*}
u\left(\mathbf{r}_1,\cdots,\mathbf{r}_n\right)&=\tilde{u}\left(\mathbf{s}_2,\cdots,\mathbf{s}_{n-1}\right)
\end{align*}
$$
そのため,$${\mathbf{s}_1}$$に関する積分は$${V}$$となる。
また,ポテンシャルエネルギーが原子間距離が離れるほど大きくなる性質を仮定しているため,$${\mathbf{s}_k\ (k=2,\cdots,n-1)}$$に関する積分は$${V}$$に依存しない。
以上より,
$$
\begin{align*}
Q(N,V,T)&=\frac{(Vf(n,T))^N}{N!}
\end{align*}
$$
となる。
c.
$$
\begin{align*}
F(N,V,T)&=-k_{\rm B}T\ln Q(N,V,T)\\
&=-k_{\rm B}T\left\{N\ln V+N+\ln f(n,T)-\ln N!\right\}
\end{align*}
$$
より,圧力$${P}$$は
$$
\begin{align*}
P&=-\left(\frac{\partial F(N,V,T)}{\partial V}\right)_{N,T}\\
&=\frac{k_{\rm B}TN}{V}\\
\therefore PV&=Nk_{\rm B}T
\end{align*}
$$
d. $${V,T}$$を固定した状態で自由エネルギー$${F(V,T,N_A,N_B,N_C,N_D)}$$を全微分すると,
$$
\begin{align*}
{\rm d}F&=\frac{\partial F}{\partial N_A}{\rm d}N_A+\frac{\partial F}{\partial N_B}{\rm d}N_B+\frac{\partial F}{\partial N_C}{\rm d}N_C+\frac{\partial F}{\partial N_D}{\rm d}N_D\\
&=\left(a\mu_A+b\mu_B-c\mu_C-d\mu_D\right){\rm d}\lambda
\end{align*}
$$
平衡状態では$${{\rm d}F=0}$$より,
$$
\begin{align*}
a\mu_A+b\mu_B-c\mu_C-d\mu_D&=0
\end{align*}
$$
が成立する。
e.
$$
\begin{align*}
Q(V,T,N_A,N_B,N_C,N_D)&=\prod_{\alpha=A,B,C,D}\frac{\{q_{\alpha}(n_{\alpha},V,T)\}^{N_{\alpha}}}{N_{\alpha}!}
\end{align*}
$$
より,
$$
\begin{align*}
\mu_{\alpha}&=-k_{\rm B}T\frac{\partial}{\partial N_{\alpha}}\left\{N_{\alpha}\ln q_{\alpha}-\ln N_{\alpha}!\right\}\\
&\simeq-k_{\rm B}T\frac{\partial}{\partial N_{\alpha}}\left\{N_{\alpha}\ln q_{\alpha}-N_{\alpha}\ln N_{\alpha}+N_{\alpha}\right\}\\
&=-k_{\rm B}T\ln\frac{q_{\alpha}}{N_{\alpha}}\\
&=-k_{\rm B}T\ln\frac{q_{\alpha}}{V\rho_{\alpha}}\\
\end{align*}
$$
この化学ポテンシャルの表式を式(4.14.27)に代入すると,
$$
\begin{align*}
a\ln\frac{q_{A}}{V\rho_{A}}+b\ln\frac{q_B}{V\rho_{B}}-c\ln\frac{q_{C}}{V\rho_{C}}-d\ln\frac{q_{D}}{V\rho_{D}}&=0\\
\ln\left\{\frac{\left(\frac{q_{A}}{V\rho_{A}}\right)^a\left(\frac{q_{B}}{V\rho_{B}}\right)^b}{\left(\frac{q_{C}}{V\rho_{C}}\right)^c\left(\frac{q_{D}}{V\rho_{D}}\right)^d}\right\}&=0\\
\frac{\left(\frac{q_{A}}{V\rho_{A}}\right)^a\left(\frac{q_{B}}{V\rho_{B}}\right)^b}{\left(\frac{q_{C}}{V\rho_{C}}\right)^c\left(\frac{q_{D}}{V\rho_{D}}\right)^d}&=1
\end{align*}
$$
$$
\begin{align*}
\therefore \frac{\rho_C^c\rho_D^d}{\rho_A^a\rho_B^b}&=\frac{(q_C/V)^c(q_D/V)^d}{(q_A/V)^a(q_B/V)^b}
\end{align*}
$$
$${q_{\alpha}=Vf_{\alpha}(n_{\alpha},T)}$$より,
$$
\begin{align*}
\therefore \frac{\rho_C^c\rho_D^d}{\rho_A^a\rho_B^b}&=\frac{\{f_C(n_C,T)\}^c\{f_D(n_D,T)\}^d}{\{f_A(n_A,T)\}^a\{f_B(n_B,T)\}^b}
\end{align*}
$$
となるため,両辺は温度$${T}$$のみの関数である。
各分子種の気体の状態方程式が理想気体となるため,
$$
\begin{align*}
\frac{\left(\frac{P_C}{k_{\rm B}T}\right)^c\left(\frac{P_D}{k_{\rm B}T}\right)^d}{\left(\frac{P_A}{k_{\rm B}T}\right)^a\left(\frac{P_B}{k_{\rm B}T}\right)^b}&=\frac{\{f_C(n_C,T)\}^c\{f_D(n_D,T)\}^d}{\{f_A(n_A,T)\}^a\{f_B(n_B,T)\}^b}\\
\therefore K&=\frac{P_C^cP_D^d}{P_A^aP_B^b}\\
&=(k_{\rm B}T)^{c+d-a-b}\frac{\{f_C(n_C,T)\}^c\{f_D(n_D,T)\}^d}{\{f_A(n_A,T)\}^a\{f_B(n_B,T)\}^b}
\end{align*}
$$
Problem 4.13
以下のペアポテンシャルを介して相互作用しているN個の同一粒子からなる系を考える。
$$
\begin{align*}
u(\mathbf{r}_1,\cdots,\mathbf{r}_N)&=\frac{1}{2}\sum_{i,j,i\neq j}u(|\mathbf{r}_i-\mathbf{r}_j|)
\end{align*}
$$
ここで,$${u(r)}$$は以下の形式で表される一般的な反発ポテンシャルである。
$$
\begin{align*}
u(r)&=\frac{A}{r^n}
\end{align*}
$$
ここで,$${n}$$は(正の)整数(∵反発ポテンシャル),$${A>0}$$である。
希薄密度の極限において,系の圧力を$${n}$$の関数として計算せよ。$${n\leq 3}$$において,系が不安定となる理由を説明せよ。
ヒント:解を表すのにガンマ関数が使えるかもしれない。
$$
\begin{align*}
\Gamma(x)&=\int_0^{\infty}{\rm d}tt^{x-1}{\rm e}^{-t}
\end{align*}
$$
また,以下のガンマ関数の性質も使えるかもしれない。
$$
\begin{align*}
\Gamma(x)&>0&x>0\\
\Gamma(0)&=\infty&x\leq 0\\
\Gamma(-n)&=\infty&{\rm for\ integer\ }n\\
\end{align*}
$$
希薄密度の極限において,動径分布関数$${g(r)}$$は
$$
\begin{align*}
g(r)&\simeq&{\rm e}^{-\beta u(r)}&={\rm e}^{-\beta Ar^{-n}}\\
\end{align*}
$$
と近似できる。
これを用いてヘルムホルツ自由エネルギーの第一摂動項$${F^{(1)}}$$を計算すると,
$$
\begin{align*}
F^{(1)}&=2\pi N\rho\int_{0}^{\infty}{\rm d}rr^2Ar^{-n}{\rm e}^{-\beta Ar^{-n}}\\
&=2\pi AN\rho\int_{0}^{\infty}{\rm d}rr^{2-n}{\rm e}^{-\beta Ar^{-n}}
\end{align*}
$$
となる。
$${t=\beta A r^{-n}}$$と変数変換すると,
$$
\begin{align*}
F^{(1)}&=\frac{2\pi (\beta A)^{3/n}N\rho}{n\beta }\int_{0}^{\infty}{\rm d}tt^{-3/n}{\rm e}^{-t}\\
&=\frac{2\pi (\beta A)^{3/n}N\rho}{n\beta }\Gamma\left(1-\frac{3}{n}\right)
\end{align*}
$$
となる。
第一摂動項まで含めた圧力$${P}$$は
$$
\begin{align*}
P&=\frac{Nk_{\rm B}T}{V}+\frac{2\pi (\beta A)^{3/n}N\rho^2}{n\beta }\Gamma\left(1-\frac{3}{n}\right)
\end{align*}
$$
と算出される。
ガンマ関数の性質により,$${n\leq 3}$$の場合に圧力は発散する。$${n}$$が小さくなるほど反発力が長距離にわたって及ぼされることになるので,$${n}$$がある値より下回ると不安定になるのはリーズナブルである。
参考文献
Mark Tuckerman, Statistical Mechanics: Theory and Molecular Simulation (Oxford Graduate Texts)
G. J. Martyna et al., Molecular Physics, 1996, Vol. 87, No. 5, 1117-1157
この記事が気に入ったらサポートをしてみませんか?
