Adiabatic free energy dynamics

状態間の自由エネルギー変化を求める分子シミュレーション法の一種であるAdiabatic free energy dynamicsを解説します。

動的変数λの導入

体積VにN個の粒子が存在し，状態A, Bがポテンシャルエネルギー

でそれぞれ記述されるとします。
次に変数λ(0 ≦ λ ≦ 1)を導入し，状態Aから状態Bの変化をλで表すポテンシャルエネルギー

を導入します。
自由エネルギー摂動法（free energy perturbation method）ではλをある値に固定したシミュレーションを複数のλに対して実施しますが，adiabatic free energy dynamicsではλを動的変数として扱い，シミュレーション中にλの値が変化します。
λを動的変数として含めたハミルトニアンは式④になります。

対応する分配関数は

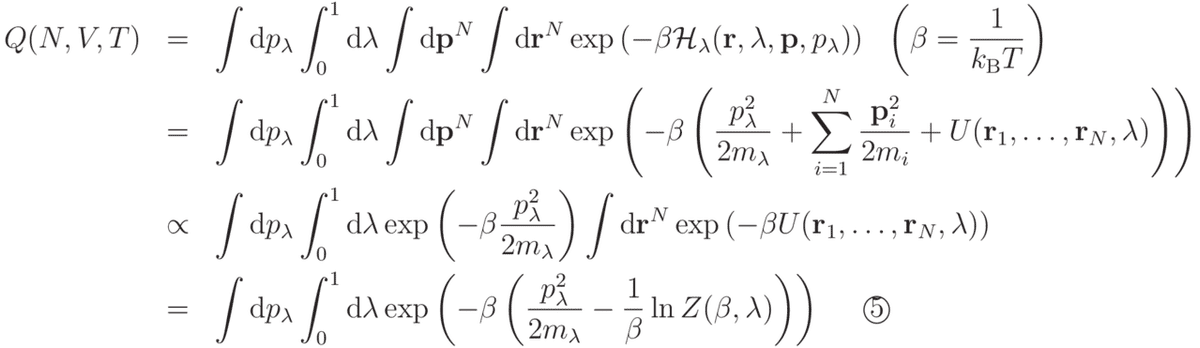
となります。
式⑤を得る際に

を導入しました。

はλに対する平均力ポテンシャルであり，この平均力ポテンシャルが求まれば目的の自由エネルギー差も求めることができます。

動的変数λはあたかも式⑥で表される有効ハミルトニアンに従うと解釈できます。

adiabatic decoupling

次にλに関するサンプリングをできる限り効率化することを考えます。
温度を上げることが運動性を高める手っ取り早い方法ですが，実粒子の温度は興味ある温度（例えば，300K）に保ちたいところです。
そこで，m_λを極端に重くする（=λの速度を極端に遅くなるようにする）ことによって，λと実粒子の運動が断熱的に分断（adiabatic decoupling）されるような状況を考えます。
そのような状況下においては，λに対してのみ高温のthermostatを適用することができるため，その温度をT_λ( >> T)とすると，adiabatic decouplingが成立する極限においてλの平均力ポテンシャルA(λ, T_λ)は

となります。
つまり，温度T_λのthermostatとcouplingしているにも関わらず，その平均力ポテンシャルは温度Tにおける平均力ポテンシャルと（λに依存しない項を除くと）一致することになります。

参考文献

　1.  Mark Tuckerman, Statistical Mechanics: Theory and Molecular Simulation (Oxford Graduate Texts)