Statistical Mechanics: Theory and Molecular Simulation Chapter 15 - The Langevin and generalized Langevin equations

nori

2024年2月23日 21:57

Statistical Mechanics: Theory and Molecular SimulationはMark Tuckermanによって著された分子シミュレーションに関連した熱・統計物理学，及び量子力学の参考書になります。

現時点では（恐らく）和訳がないこともあり，日本での知名度はあまりないような気がしますが，被引用数が1500を超えていることを考えると海外では高く認知されている参考書みたいです。

https://scholar.google.com/citations?user=w_7furwAAAAJ

本記事では，Chapter 15（The Langevin and generalized Langevin equations）の章末問題の和訳とその解答例を紹介します。解答例に間違いが見受けられた場合はお知らせいただけると助かります。

Problem 15.1

(15.2.11)式で与えられる調和浴モデルの$${R(t)}$$を用いて$${\langle q(0)R(t)\rangle=0}$$を示し，また(15.2.17)式を導出せよ。

$$
\begin{align*}
R(t)&=-\sum_{\alpha}g_{\alpha}\left[\left(x_{\alpha}(0)+\frac{g_{\alpha}}{m_{\alpha}\omega_{\alpha}^2}q(0)\right)\cos\omega_{\alpha}t\right.\\
&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left.+\frac{p_{\alpha}(0)}{m_{\alpha}\omega_{\alpha}}\sin\omega_{\alpha}t\right]
\end{align*}\tag{15.2.11}
$$

$$
\begin{align*}
\langle R(0)R(t)\rangle&=\frac{1}{\beta}\sum_{\alpha}\frac{g_{\alpha}^2}{m_{\alpha}\omega_{\alpha}^2}\cos\omega_{\alpha}t&=k_{\rm B}T\zeta(t)
\end{align*}\tag{15.2.17}
$$

$$
\begin{align*}
\langle q(0)R(t)\rangle&\propto-\int{\rm d}p{\rm d}q\exp\left\{-\beta\left[\frac{p^2}{2\mu^2}+V(q)\right]\right\}\\
&\times q\sum_{\alpha}g_{\alpha}\cos\omega_{\alpha}t\prod_{\beta=1}^n\int{\rm d}x_{\beta}\left(x_{\alpha}+\frac{g_{\alpha}q}{m_{\alpha}\omega_{\alpha}}\right)\exp\left\{-\frac{\beta m_{\beta}\omega_{\beta}}{2}\left(x_{\beta}+\frac{g_{\beta}q}{m_{\beta}\omega_{\beta}}\right)^2\right\}\\
&\times q\sum_{\alpha}\frac{g_{\alpha}\sin\omega_{\alpha}t}{m_{\alpha}\omega_{\alpha}}\prod_{\beta=1}^n\int{\rm d}p_{\beta}p_{\alpha}\exp\left(-\frac{\beta p_{\beta}^2}{2m_{\beta}}\right)\\
&\propto-\int{\rm d}p{\rm d}q\exp\left\{-\beta\left[\frac{p^2}{2\mu^2}+V(q)\right]\right\}\\
&\times q\sum_{\alpha}g_{\alpha}\cos\omega_{\alpha}t\prod_{\beta=1}^n(1-\delta_{\alpha\beta})\sqrt{\frac{2\pi}{\beta m_{\beta}\omega_{\beta}}}\\
&\times q\sum_{\alpha}\frac{g_{\alpha}\sin\omega_{\alpha}t}{m_{\alpha}\omega_{\alpha}}\prod_{\beta=1}^n(1-\delta_{\alpha\beta})\sqrt{\frac{2m_{\beta}\pi}{\beta}}\\
&\propto 0
\end{align*}\tag{1.1}
$$

$$
\begin{align*}
\therefore \langle q(0)R(t)\rangle&= 0
\end{align*}\tag{1.2}
$$

$$
\begin{align*}
R(0)R(t)&= \sum_{\alpha,\beta}g_{\alpha}g_{\beta}\left(x_{\beta}(0)+\frac{g_{\beta}q(0)}{m_{\beta}\omega_{\beta}}\right)\\
&\times\left[\left(x_{\alpha}(0)+\frac{g_{\alpha}q(0)}{m_{\alpha}\omega_{\alpha}}\right)\cos\omega_{\alpha}t+\frac{p_{\alpha}(0)}{m_{\alpha}\omega_{\alpha}}\sin\omega_{\alpha}t\right]
\end{align*}\tag{1.3}
$$

となるが，(1.3)式の右辺の第二項は$${\int{\rm d}p_{\alpha}p_{\alpha}\exp(-\beta p_{\alpha}^2/2m_{\alpha})=0}$$となる。
また，(1.3)式の右辺の第一項も$${\alpha\neq\beta}$$においては同様に0となるため，

$$
\begin{align*}
\langle R(0)R(t)\rangle&= \left\langle\sum_{\alpha}g_{\alpha}^2\left(x_{\alpha}(0)+\frac{g_{\alpha}q(0)}{m_{\alpha}\omega_{\alpha}}\right)^2\cos\omega_{\alpha}t\right\rangle\\
&=\frac{\sum_{\alpha}g_{\alpha}^2\cos\omega_{\alpha}t\int{\rm d}q{\rm e}^{-\beta V(q)}\prod_{\beta=1}^n{\rm e}^{-\frac{\beta g_{\beta}^2q^2}{2m_{\beta}\omega_{\beta}^2}}\int{\rm d}x_{\beta}\left(x_{\alpha}+\frac{g_{\alpha}q}{m_{\alpha}\omega_{\alpha}^2}\right)^2{\rm e}^{-\frac{\beta m_{\beta}\omega_{\beta}^2}{2}\left(x_{\beta}+\frac{g_{\beta}q}{m_{\beta}\omega_{\beta}^2}\right)^2}}{\int{\rm d}q{\rm e}^{-\beta V(q)}\prod_{\alpha=1}^n{\rm e}^{-\frac{\beta g_{\alpha}^2q^2}{2m_{\alpha}\omega_{\alpha}^2}}\int{\rm d}x_{\alpha}{\rm e}^{-\frac{\beta m_{\alpha}\omega_{\alpha}^2}{2}\left(x_{\alpha}+\frac{g_{\alpha}q}{m_{\alpha}\omega_{\alpha}^2}\right)^2}}\\
&=\frac{\sum_{\alpha}\frac{g_{\alpha}^2\cos\omega_{\alpha}t}{\beta m_{\alpha}\omega_{\alpha}}\int{\rm d}q{\rm e}^{-\beta V(q)}\prod_{\beta=1}^n{\rm e}^{-\frac{\beta g_{\beta}^2q^2}{2m_{\beta}\omega_{\beta}^2}}\sqrt{\frac{2\pi}{\beta m_{\beta}\omega_{\beta}^2}}}{\int{\rm d}q{\rm e}^{-\beta V(q)}\prod_{\alpha=1}^n{\rm e}^{-\frac{\beta g_{\alpha}^2q^2}{2m_{\alpha}\omega_{\alpha}^2}}\sqrt{\frac{2\pi}{\beta m_{\alpha}\omega_{\alpha}^2}}}\\
&=\frac{1}{\beta}\sum_{\alpha}\frac{g_{\alpha}^2}{m_{\alpha}\omega_{\alpha}^2}\cos\omega_{\alpha}t
\end{align*}\tag{1.4}
$$

Problem 15.2

一般化ランジュバン方程式に従う質量$${m}$$を有する単一の調和振動子の自由度$${q}$$を考える。

$$
\begin{align*}
\ddot{q}&=-\omega^2 q-\int_{0}^t{\rm d}\tau\dot{q}(\tau)\gamma(t-\tau)+f(t)
\end{align*}
$$

ここで，$${\omega}$$は$${q}$$の振動数である。また，$${\gamma(t)=\zeta(t)/m}$$，$${f(t)=R(t)/m}$$であり，$${R(t)}$$はランダム力，$${\zeta(t)}$$は摩擦カーネルを意味する。摩擦カーネルが速やかに減衰するcrudeモデルとして，$${\gamma(t)}$$が短時間$${t_0}$$において一定値を取り，その後に瞬間的に$${0}$$となる場合を考える。

$$
\begin{align*}
\gamma(t)&=\gamma_0\theta(t_0-t)
\end{align*}
$$

ここで，$${\gamma_0}$$は定数，$${\theta(t)}$$はヘヴィサイトステップ関数である。また，$${t,t_0\geq0}$$を満たす。

a. もし$${t_0}$$が$${\exp(-s t_0)\simeq 1-st_0}$$と近似できる程度に小さい場合，この系のメモリの存在によって規格化された速度自己相関関数$${C_{vv}(t)}$$が$${\omega}$$より小さい振動数で振動し，かつ時間に対して緩やかに減衰することを示し，$${C_{vv}(t)}$$の減衰定数と振動数を決定せよ。

b. ここでは$${t_0}$$がとても大きい場合を想定する。この場合においては速度自己相関関数は減衰しないが，$${\omega}$$とは異なる振動数で振動することを示し，$${C_{vv}(t)}$$と振動数を決定せよ。

c. a.とb.で考えた２つの場合に対する速度自己相関関数の振る舞いの物理的起源を説明せよ。

与えられた一般化ランジュバン方程式の両辺をラプラス変換すると，

$$
\begin{align*}
s^2\tilde{q}(s)-\dot{q}(0)-sq(0)&=-\omega^2\tilde{q}(s)-\left[s\tilde{q}(s)-q(0)\right]\tilde{\gamma}(s)+\tilde{f}(s)
\end{align*}\tag{2.1}
$$

となる。
$${\tilde\gamma(s)}$$を具体的に計算すると(2.2)式となる。

$$
\begin{align*}
\tilde{\gamma}(s)&=\int_{0}^{\infty}{\rm d}s{\rm e}^{-st}\gamma(t)\\
&=\gamma_0\int_{0}^{t_0}{\rm d}s{\rm e}^{-st}\\
&=\frac{\gamma_0}{s}\left(1-{\rm e}^{-st_0}\right)
\end{align*}\tag{2.2}
$$

a. $${\exp(-s t_0)\simeq 1-st_0}$$，及び(2.2)式を(2.1)式に代入すると，

$$
\begin{align*}
s^2\tilde{q}(s)-\dot{q}(0)-sq(0)&=-\omega^2\tilde{q}(s)-\left[s\tilde{q}(s)-q(0)\right]\gamma_0 t_0+\tilde{f}(s)
\end{align*}\tag{2.3}
$$

となる。
$${\omega_0^2:=\omega^2-\gamma_0^2t_0^2/4,\ s_0:=s+\gamma_0t_0/2}$$として(2.3)式を式変形すると，

$$
\begin{align*}
\left(s_0^2+\omega_0^2\right)\tilde{q}(s_0-\gamma_0t_0/2)&=\dot{q}(0)-(s_0+\gamma_0t_0/2)q(0)\\
&\ \ \ \ \ \ \ \ \ \ +\tilde{f}(s_0-\gamma_0t_0/2)
\end{align*}\tag{2.4}
$$

$$
\begin{align*}
\therefore \tilde{q}(s_0-\gamma_0t_0/2)&=\frac{\dot{q}(0)}{s_0^2+\omega_0^2}+\frac{(s_0+\gamma_0t_0/2)q(0)}{s_0^2+\omega_0^2}\\
&\ \ \ \ \ \ \ \ \ \ +\frac{\tilde{f}(s_0-\gamma_0t_0/2)}{s_0^2+\omega_0^2}
\end{align*}\tag{2.5}
$$

(2.5)式の両辺を逆ラプラス変換することにより，$${q(t)}$$が求まる。

$$
\begin{align*}
q(t){\rm e}^{\gamma_0t_0t/2}&=\frac{\dot{q}(0)}{\omega_0}\sin\omega_0 t+q(0)\cos\omega_0 t+\frac{\gamma_0t_0q(0)}{2\omega_0}\sin\omega_0 t\\
&\ \ \ \ \ \ \ \ \ \ +\frac{1}{\omega_0}\int_0^t{\rm d}\tau f(\tau){\rm e}^{\gamma_0t_0\tau/2}\sin\omega_0(t-\tau)\\
&=\frac{\dot{q}(0)+\gamma_0t_0q(0)/2}{\omega_0}\sin\omega_0 t+q(0)\cos\omega_0 t\\
&\ \ \ \ \ \ \ \ \ \ +\frac{1}{\omega_0}\int_0^t{\rm d}\tau f(\tau){\rm e}^{\gamma_0t_0\tau/2}\sin\omega_0(t-\tau)\\
\end{align*}\tag{2.6}
$$

$$
\begin{align*}
\therefore q(t)&=\left\{\frac{\dot{q}(0)+\gamma_0t_0q(0)/2}{\omega_0}\sin\omega_0 t+q(0)\cos\omega_0 t\right.\\
&\ \ \ \ \ \ \ \ \ \ +\left.\frac{1}{\omega_0}\int_0^t{\rm d}\tau f(\tau){\rm e}^{\gamma_0t_0\tau/2}\sin\omega_0(t-\tau)\right\}{\rm e}^{-\gamma_0t_0t/2}\\
\end{align*}\tag{2.7}
$$

(2.7)式の両辺を$${t}$$で微分すると，

$$
\begin{align*}
\dot{q}(t)&=\left\{\dot{q}(0)\cos\omega_0 t\right.\\
&\ \ \ \ \ \ \ \ \ \ -\left[\frac{\gamma_0t_0}{2\omega_0}\left(\dot{q}(0)+\frac{\gamma_0 t_0q(0)}{2}\right)+q(0)\omega_0\right]\sin\omega_0 t\\
&\ \ \ \ \ \ \ \ \ \ -\frac{\gamma_0t_0}{2\omega_0}\int_0^t{\rm d}\tau f(\tau){\rm e}^{\gamma_0t_0\tau/2}\sin\omega_0(t-\tau)\\
&\ \ \ \ \ \ \ \ \ \ \left.\int_0^t{\rm d}\tau f(\tau){\rm e}^{\gamma_0t_0\tau/2}\cos\omega_0(t-\tau)\right\}{\rm e}^{-\gamma_0t_0t/2}\\
\end{align*}\tag{2.8}
$$

$$
\begin{align*}
&\therefore C_{vv}(t)\\
&=\langle\dot{q}(0)\dot{q}(t)\rangle\\
&=\left\{\langle\dot{q}^2\rangle\cos\omega_0 t\right.\\
&\ \ \ \ \ \ \ \ \ \ -\left.\left[\frac{\gamma_0t_0}{2\omega_0}\left(\langle\dot{q}^2\rangle+\frac{\gamma_0 t_0\langle\dot{q}q\rangle}{2}\right)+\langle\dot{q}q\rangle\omega_0\right]\sin\omega_0 t\right\}{\rm e}^{-\gamma_0t_0t/2}\\
\end{align*}\tag{2.9}
$$

以上より，$${C_{vv}(t)}$$は減衰定数$${\gamma_0t_0/2}$$，振動数$${\omega_0=\sqrt{\omega^2-\gamma_0^2t_0^2/4}\ (<\omega)}$$で減衰振動する。

b. $${\exp(-s t_0)\simeq 0}$$，及び(2.2)式を(2.1)式に代入すると，

$$
\begin{align*}
s^2\tilde{q}(s)-\dot{q}(0)-sq(0)&=-\omega^2\tilde{q}(s)-\left[\tilde{q}(s)-\frac{q(0)}{s}\right]\gamma_0+\tilde{f}(s)
\end{align*}\tag{2.10}
$$

となる。
$${\omega_1^2:=\omega^2+\gamma_0}$$として(2.10)式を式変形すると，

$$
\begin{align*}
\tilde{q}(s)&=\frac{\dot{q}(0)}{s^2+\omega_1^2}+\frac{sq(0)}{s^2+\omega_1^2}+\frac{\gamma_0q(0)}{s(s^2+\omega_1^2)}+\frac{\tilde{f}(s)}{s^2+\omega_1^2}
\end{align*}\tag{2.11}
$$

(2.11)式を逆ラプラス変換することで$${q(t)}$$が得られる。

$$
\begin{align*}
q(t)&=\frac{\dot{q}(0)}{\omega_1}\sin\omega_1 t+q(0)\cos\omega_1 t+\frac{\gamma_0q(0)}{\omega_1}\int_{0}^t{\rm d}\tau\sin\omega_1\tau\\
&\ \ \ \ \ \ \ \ +\frac{1}{\omega_1}\int_{0}^t{\rm d}\tau f(\tau)\sin\omega_1(t-\tau)
\end{align*}\tag{2.12}
$$

$$
\begin{align*}
\dot{q}(t)&=\dot{q}(0)\cos\omega_1 t-\omega_1 q(0)\sin\omega_1 t+\frac{\gamma_0q(0)}{\omega_1}\sin\omega_1t\\
&\ \ \ \ \ \ \ \ +\int_{0}^t{\rm d}\tau f(\tau)\cos\omega_1(t-\tau)\\
&=\dot{q}(0)\cos\omega_1 t+\left(\frac{\gamma_0}{\omega_1}-\omega_1\right)q(0)\sin\omega_1 t+\sin\omega_1t\\
&\ \ \ \ \ \ \ \ +\int_{0}^t{\rm d}\tau f(\tau)\cos\omega_1(t-\tau)
\end{align*}\tag{2.13}
$$

$$
\begin{align*}
\therefore C_{vv}(t)&=\langle\dot{q}(0)\dot{q}(t)\rangle\\
&=\langle\dot{q}^2\rangle\cos\omega_1 t+\left(\frac{\gamma_0}{\omega_1}-\omega_1\right)\langle\dot{q}q\rangle\sin\omega_1 t
\end{align*}\tag{2.14}
$$

以上より，$${C_{vv}(t)}$$は振動数$${\omega_1=\sqrt{\omega^2+\gamma_0}\ (\neq\omega)}$$で振動する。

c. $${t_0\ll 1}$$の場合，メモリ積分の項は摩擦力と見なすことができる。一方，$${t_0\gg 1}$$の場合，メモリ積分の項は$${\propto\int{\rm d}t\dot{q}=q(t)}$$となり，振動数を変動させる効果をもたらす。

Problem 15.3

電子移動の単純モデルは，以下の形式の量子ハミルトニアンで定義される。

$$
\begin{align*}
\hat{\mathcal{H}}&=\frac{\varepsilon}{2}\sigma_z+\frac{\Delta}{2}\sigma_x
\end{align*}
$$

ここで，$${\varepsilon,\ \Delta}$$は定数であり，$${\sigma_x,\ \sigma_y,\ \sigma_z}$$は以下で与えられる。

$$
\begin{align*}
\sigma_x=\begin{bmatrix}0&1\\1&0\end{bmatrix}\ \ \ \sigma_y=\begin{bmatrix}0&-{\rm i}\\{\rm i}&0\end{bmatrix}\ \ \ \sigma_z=\begin{bmatrix}1&0\\0&-1\end{bmatrix}
\end{align*}
$$

このモデルでは電子には２つの状態しかないと仮定しており，それゆえこのモデルは本当の電子移動問題を単純化したものである。

a. ハイゼンベルク描像において，時間発展する系の可観測量を表す演算子は以下の運動方程式に従う。

$$
\begin{align*}
\frac{{\rm d}\hat{A}}{{\rm d}t}&=\frac{1}{{\rm i}\hbar}\left[\hat{A},\hat{\mathcal{H}}\right]
\end{align*}
$$

ここで，$${\hat{A}}$$は任意の演算子である。$${\sigma_x,\ \sigma_y,\ \sigma_z}$$に対するハイゼンベルクの運動方程式を書き下せ。

b. 初期条件がカノニカル分布である場合の自己相関関数$${\langle\sigma_y(0)\sigma_y(t)\rangle}$$を計算せよ。

c. 環境からの影響を模擬するため，上記の２準位系を量子力学的調和振動子の浴と接触させる。この場合のハミルトニアンは以下で与えられる。

$$
\begin{align*}
\hat{\mathcal{H}}&=\frac{\varepsilon}{2}\sigma_z+\frac{\Delta}{2}\sigma_x+\sum_{\alpha}\hbar\omega_{\alpha}\left[\hat{a}_{\alpha}^{\dagger}\hat{a}_{\alpha}+\frac{1}{2}\right]+\frac{\hbar}{2}\sigma_z\sum_{\alpha}g_{\alpha}\left(\hat{a}_{\alpha}^{\dagger}+\hat{a}_{\alpha}\right)
\end{align*}
$$

$${\alpha}$$は浴の各振動モードに割り当てられるインデックス，$${\omega_{\alpha}}$$は浴の振動モードの振動数，$${\hat{a}_{\alpha},\ \hat{a}_{\alpha}^{\dagger}}$$はそれぞれ浴の消滅・生成演算子，$${g_{\alpha}}$$は結合定数を表す。このハミルトニアンに対する，$${\sigma_x,\ \sigma_y,\ \sigma_z,\ \hat{a}_{\alpha},\ \hat{a}_{\alpha}^{\dagger}}$$のハイゼンベルグの運動方程式を書き下せ。

d. $${\hat{a}_{\alpha},\ \hat{a}_{\alpha}^{\dagger}}$$に対するハイゼンベルグの運動方程式を解くことにより，スピン演算子$${\sigma_x,\ \sigma_y}$$に対する一般化ランジュバン形の方程式を構築せよ。

$$
\begin{align*}
\dot{\sigma}_x&=\frac{1}{{\rm i}\hbar}\left[\sigma_x, \frac{\varepsilon}{2}\sigma_z+\frac{\Delta}{2}\sigma_x\right]\\
&=\frac{\varepsilon}{2{\rm i}\hbar}\left[\sigma_x,\sigma_z\right]+\frac{\Delta}{2{\rm i}\hbar}\left[\sigma_x,\sigma_x\right]\\
&=-\frac{\varepsilon}{\hbar}\sigma_y\\
\dot{\sigma}_y&=\frac{1}{{\rm i}\hbar}\left[\sigma_y, \frac{\varepsilon}{2}\sigma_z+\frac{\Delta}{2}\sigma_x\right]\\
&=\frac{\varepsilon}{2{\rm i}\hbar}\left[\sigma_y,\sigma_z\right]+\frac{\Delta}{2{\rm i}\hbar}\left[\sigma_y,\sigma_x\right]\\
&=\frac{\varepsilon}{\hbar}\sigma_x-\frac{\Delta}{\hbar}\sigma_z\\
\dot{\sigma}_z&=\frac{1}{{\rm i}\hbar}\left[\sigma_z, \frac{\varepsilon}{2}\sigma_z+\frac{\Delta}{2}\sigma_x\right]\\
&=\frac{\varepsilon}{2{\rm i}\hbar}\left[\sigma_z,\sigma_z\right]+\frac{\Delta}{2{\rm i}\hbar}\left[\sigma_z,\sigma_x\right]\\
&=\frac{\Delta}{\hbar}\sigma_y\\
\end{align*}\tag{3.1}
$$

b. 以下の条件を満たす状態ベクトル$${|\uparrow\rangle, |\downarrow\rangle}$$を導入する。

$$
\begin{align*}
\sigma_x|\uparrow\rangle&=|\downarrow\rangle\\
\sigma_x|\downarrow\rangle&=|\uparrow\rangle\\
\sigma_y|\uparrow\rangle&={\rm i}|\downarrow\rangle\\
\sigma_y|\downarrow\rangle&=-{\rm i}|\uparrow\rangle\\
\sigma_z|\uparrow\rangle&=|\uparrow\rangle\\
\sigma_z|\downarrow\rangle&=-|\downarrow\rangle\\
\end{align*}\tag{3.2}
$$

このとき，

$$
\begin{align*}
\langle\uparrow|{\rm e}^{-\beta\hat{\mathcal{H}}}\sigma_y(0)\sigma_y(t)|\uparrow\rangle&=\langle\uparrow|{\rm e}^{-\beta\hat{\mathcal{H}}}\sigma_y{\rm e}^{{\rm i}\hat{\mathcal{H}}t/\hbar}\sigma_y{\rm e}^{-{\rm i}\hat{\mathcal{H}}t/\hbar}|\uparrow\rangle\\
&=\langle\uparrow|{\rm e}^{-{\rm i}\hat{\mathcal{H}}t/\hbar}{\rm e}^{-\beta\hat{\mathcal{H}}}\sigma_y{\rm e}^{{\rm i}\hat{\mathcal{H}}t/\hbar}\sigma_y|\uparrow\rangle\\
&={\rm i}\langle\uparrow|{\rm e}^{-{\rm i}\hat{\mathcal{H}}t/\hbar}{\rm e}^{-\beta\hat{\mathcal{H}}}\sigma_y{\rm e}^{{\rm i}\hat{\mathcal{H}}t/\hbar}|\downarrow\rangle\\
&={\rm i}\langle\uparrow|{\rm e}^{-\beta\hat{\mathcal{H}}}\sigma_y|\downarrow\rangle\\
&=\langle\uparrow|{\rm e}^{-\beta\hat{\mathcal{H}}}|\uparrow\rangle\\
\langle\downarrow|{\rm e}^{-\beta\hat{\mathcal{H}}}\sigma_y(0)\sigma_y(t)|\downarrow\rangle&=\langle\downarrow|{\rm e}^{-\beta\hat{\mathcal{H}}}|\downarrow\rangle\\
\end{align*}\tag{3.3}
$$

$$
\begin{align*}
\therefore \langle\sigma_y(0)\sigma_y(t)\rangle&=\frac{{\rm Tr}\left[{\rm e}^{-\beta\hat{\mathcal{H}}}\sigma_y(0)\sigma_y(t)\right]}{{\rm Tr}\left[{\rm e}^{-\beta\hat{\mathcal{H}}}\right]}\\
&=\frac{{\rm Tr}\left[{\rm e}^{-\beta\hat{\mathcal{H}}}\right]}{{\rm Tr}\left[{\rm e}^{-\beta\hat{\mathcal{H}}}\right]}\\
&=1\ (?)
\end{align*}\tag{3.4}
$$

$$
\begin{align*}
\dot{\sigma}_x&=-\left(\frac{\varepsilon}{\hbar}+\sum_{\alpha}g_{\alpha}\left(\hat{a}_{\alpha}^{\dagger}+\hat{a}_{\alpha}\right)\right)\sigma_y\\
\dot{\sigma}_y&=\left(\frac{\varepsilon}{\hbar}+\sum_{\alpha}g_{\alpha}\left(\hat{a}_{\alpha}^{\dagger}+\hat{a}_{\alpha}\right)\right)\sigma_x-\frac{\Delta}{\hbar}\sigma_z\\
\dot{\sigma}_z&=\frac{\Delta}{\hbar}\sigma_y\\
\dot{\hat{a}}_{\alpha}&=-{\rm i}\omega_{\alpha}\hat{a}_{\alpha}-{\rm i}\frac{g_{\alpha}}{2}\sigma_z\\
\dot{\hat{a}}_{\alpha}^{\dagger}&={\rm i}\omega_{\alpha}\hat{a}_{\alpha}^{\dagger}+{\rm i}\frac{g_{\alpha}}{2}\sigma_z\\
\end{align*}\tag{3.5}
$$

d. $${\hat{a}_{\alpha}}$$が満たす運動方程式の両辺をラプラス変換する。

$$
\begin{align*}
s\tilde{\hat{a}}_{\alpha}(s)-\hat{a}_{\alpha}(0)&=-{\rm i}\omega_{\alpha}\tilde{\hat{a}}_{\alpha}(s)-{\rm i}\frac{g_{\alpha}}{2}\tilde{\sigma}_z(s)\\
\therefore \tilde{\hat{a}}_{\alpha}(s)&=\frac{\hat{a}_{\alpha}(0)}{s+{\rm i}\omega_{\alpha}}-{\rm i}\frac{g_{\alpha}}{2}\frac{\tilde{\sigma}_z(s)}{s+{\rm i}\omega_{\alpha}}
\end{align*}\tag{3.6}
$$

(3.6)式の両辺を逆ラプラス変換することにより$${\hat{a}_{\alpha}(t)}$$が求まる。

$$
\begin{align*}
\hat{a}_{\alpha}(t)&=\hat{a}_{\alpha}(0){\rm e}^{-{\rm i}\omega_{\alpha} t}-{\rm i}\frac{g_{\alpha}}{2}\int_{0}^t{\rm d}\tau\sigma_z(\tau){\rm e}^{-{\rm i}\omega_{\alpha}(t-\tau)}
\end{align*}\tag{3.7}
$$

同様の手順で$${\hat{a}_{\alpha}^{\dagger}(t)}$$を求めると，

$$
\begin{align*}
\hat{a}_{\alpha}^{\dagger}(t)&=\hat{a}_{\alpha}^{\dagger}(0){\rm e}^{{\rm i}\omega_{\alpha} t}+{\rm i}\frac{g_{\alpha}}{2}\int_{0}^t{\rm d}\tau\sigma_z(\tau){\rm e}^{{\rm i}\omega_{\alpha}(t-\tau)}
\end{align*}\tag{3.8}
$$

Problem 15.4

調和振動子の自由度$${q}$$が以下の一般化ランジュバン方程式に従うとする。

$$
\begin{align*}
\ddot{q}&=-\tilde{\omega}^2q-\int_{0}^{\tau}{\rm d}\tau\dot{q}(\tau)\gamma(t-\tau)+f(t)
\end{align*}
$$

ここで$${\omega}$$が$${q}$$の振動数，$${\gamma(t):=\zeta(t)/m,\ f(t):=R(t)/m}$$，$${R(t)}$$はランダム力，$${\zeta(t)}$$は摩擦カーネルである。
$${\gamma(t)}$$のラプラス変換を$${\tilde{\gamma}(s)}$$とすると，$${\tilde{\omega}\gg s\tilde{\gamma}(s)}$$において一般化ランジュバン方程式の解は以下のようになる。

$$
\begin{align*}
q(t)&=q(0){\rm e}^{-\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]t/2}\left[\cos\Omega t+\frac{\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]}{2\Omega}\sin\Omega t\right]+\frac{\dot{q}(0)}{\Omega}{\rm e}^{-\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]t/2}\sin\Omega t\\
&\ \ \ \ \ \ \ \ \ \ \ +\frac{1}{\Omega}\int_0^{t}{\rm d}\tau f(t-\tau){\rm e}^{-\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]\tau/2}\sin\Omega \tau\\
\dot{q}(t)&=\dot{q}(0){\rm e}^{-\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]t/2}\left[\cos\Omega t-\frac{\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]}{2\Omega}\sin\Omega t\right]-q(0)\Omega{\rm e}^{-\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]t/2}\sin\Omega t\\
&\ \ \ \ \ \ \ \ \ \ \ +\int_0^{t}{\rm d}\tau f(t-\tau){\rm e}^{-\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]t/2}\left[\cos\Omega t-\frac{\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]}{2\Omega}\sin\Omega t\right]\\
\Omega&=\tilde{\omega}+\frac{1}{2}\Im[\tilde{\gamma}(-{\rm i}\tilde{\omega})]
\end{align*}
$$

a. $${q(t),\ \dot{q}(t)}$$が以下のように規格化された相関関数を用いて表現できることを示せ。

$$
\begin{align*}
q(t)&=q(0)C_{qq}(t)+\dot{q}(0)C_{vq}(t)+\int_0^t{\rm d}\tau f(t-\tau)C_{vq}(\tau)\\
\dot{q}(t)&=\dot{q}(0)C_{vv}(t)+q(0)C_{qv}(t)+\int_0^t{\rm d}\tau f(t-\tau)C_{vv}(\tau)\\
C_{ab}(t)&:=\frac{\langle a(0)b(t)\rangle}{\langle a^2\rangle}
\end{align*}
$$

b. $${\Omega\simeq\tilde{\omega}\ (\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})], \Im[\tilde{\gamma}(-{\rm i}\tilde{\omega})]\ll \Omega)}$$において，調和振動子の内部エネルギー

$$
\begin{align*}
\varepsilon(t)&=\frac{1}{2}\mu \dot{q}^2(t)+\frac{1}{2}\mu\tilde{\omega}^2q^2(t)
\end{align*}
$$

の自己相関関数が

$$
\begin{align*}
C_{\varepsilon\varepsilon}(t)&=\frac{1}{2}C_{vv}^2(t)+\frac{1}{2}C_{qq}^2(t)+\frac{1}{\tilde{\omega}^2}C_{qv}^2(t)
\end{align*}
$$

となることを示せ。

a. $${\langle q\dot{q}\rangle=\langle \dot{q}q\rangle=0, \langle q(0)f(t)\rangle=0, \langle \dot{q}(0)f(t)\rangle=0}$$より，

$$
\begin{align*}
C_{qq}(t)&={\rm e}^{-\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]t/2}\left[\cos\Omega t+\frac{\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]}{2\Omega}\sin\Omega t\right]\\
C_{vq}(t)&=\frac{1}{\Omega}{\rm e}^{-\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]t/2}\sin\Omega t\\
C_{vv}(t)&={\rm e}^{-\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]t/2}\left[\cos\Omega t-\frac{\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]}{2\Omega}\sin\Omega t\right]\\
C_{qv}(t)&=-\Omega{\rm e}^{-\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]t/2}\sin\Omega t
\end{align*}\tag{4.1}
$$

となる。
以上より，題意は示された。

b. 平均を取った際に0となる項をother termsとすると，

$$
\begin{align*}
\varepsilon(t)&=\frac{\mu}{2}\left\{\left[C_{vv}^2(t)+\tilde{\omega}^2C_{vq}^2(t)\right]\dot{q}^2(0)+\left[C_{qv}^2(t)+\tilde{\omega}^2C_{qq}^2(t)\right]q^2(0)\right\}\\
&\ \ \ \ +({\rm other\ therms})\\
\end{align*}\tag{4.2}
$$

となるため，

$$
\begin{align*}
&\langle\varepsilon(0)\varepsilon(t)\rangle\\
&=\frac{\mu^2}{4}\left[C_{vv}^2(t)+\tilde{\omega}^2C_{vq}^2(t)\right]\langle\dot{q}^4\rangle+\frac{\mu^2\tilde{\omega}^2}{4}\left[C_{qv}^2(t)+\tilde{\omega}^2C_{qq}^2(t)\right]\langle q^4\rangle\\
&\ \ \ \ \ +\frac{\mu^2}{4}\left\{\tilde{\omega}^2\left[C_{vv}^2(t)+\tilde{\omega}^2C_{vq}^2(t)\right]+\left[C_{qv}^2(t)+\tilde{\omega}^2C_{qq}^2(t)\right]\right\}\langle\dot{q}^2q^2\rangle
\end{align*}\tag{4.3}
$$

と式変形される。
$${\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})], \Im[\tilde{\gamma}(-{\rm i}\tilde{\omega})]\ll \Omega}$$の場合，

$$
\begin{align*}
C_{qq}(t)&\simeq C_{vv}(t)\\
C_{vq}(t)&\simeq\frac{1}{\tilde{\omega}^2}C_{qv}(t)
\end{align*}\tag{4.4}
$$

より，

$$
\begin{align*}
C_{vv}^2(t)+\tilde{\omega}^2C_{vq}^2(t)&\simeq C_{vv}^2(t)+\frac{1}{\tilde{\omega}^2}C_{qv}^2(t)\\
&=\frac{1}{2}C_{vv}^2(t)+\frac{1}{2}C_{vv}^2(t)+\frac{1}{\tilde{\omega}^2}C_{qv}^2(t)\\
&\simeq\frac{1}{2}C_{vv}^2(t)+\frac{1}{2}C_{qq}^2(t)+\frac{1}{\tilde{\omega}^2}C_{qv}^2(t)\\
\end{align*}\tag{4.5}
$$

$$
\begin{align*}
C_{qv}^2(t)+\tilde{\omega}^2C_{qq}^2(t)&=\tilde{\omega}^2\left(C_{qq}^2(t)+\frac{1}{\tilde{\omega}^2}C_{qv}^2(t)\right)\\
&\simeq\tilde{\omega}^2\left(\frac{1}{2}C_{vv}^2(t)+\frac{1}{2}C_{qq}^2(t)+\frac{1}{\tilde{\omega}^2}C_{qv}^2(t)\right)
\end{align*}\tag{4.6}
$$

$$
\begin{align*}
&\tilde{\omega}^2\left[C_{vv}^2(t)+\tilde{\omega}^2C_{vq}^2(t)\right]+\left[C_{qv}^2(t)+\tilde{\omega}^2C_{qq}^2(t)\right]\\
&\simeq\tilde{\omega}^2\left[C_{vv}^2(t)+C_{qv}^2(t)\right]+\left[C_{qv}^2(t)+\tilde{\omega}^2C_{qq}^2(t)\right]\\
&=2\tilde{\omega}^2\left(\frac{1}{2}C_{vv}^2(t)+\frac{1}{2}C_{qq}^2(t)+\frac{1}{\tilde{\omega}^2}C_{qv}^2(t)\right)
\end{align*}\tag{4.7}
$$

(5.4)-(5.6)式を(5.3)式に代入すると，

$$
\begin{align*}
&\langle\varepsilon(0)\varepsilon(t)\rangle\\
&=\frac{\mu^2}{4}\left(\langle\dot{q}^4\rangle+2\tilde{\omega}^2\langle\dot{q}^2q^2\rangle+\tilde{\omega}^4\langle q^4\rangle\right)\left(\frac{1}{2}C_{vv}^2(t)+\frac{1}{2}C_{qq}^2(t)+\frac{1}{\tilde{\omega}^2}C_{qv}^2(t)\right)\\
&=\langle\varepsilon^2\rangle\left(\frac{1}{2}C_{vv}^2(t)+\frac{1}{2}C_{qq}^2(t)+\frac{1}{\tilde{\omega}^2}C_{qv}^2(t)\right)\\
\therefore C_{\varepsilon\varepsilon}(t)&=\frac{\langle\varepsilon(0)\varepsilon(t)\rangle}{\langle\varepsilon^2\rangle}\\
&=\frac{1}{2}C_{vv}^2(t)+\frac{1}{2}C_{qq}^2(t)+\frac{1}{\tilde{\omega}^2}C_{qv}^2(t)
\end{align*}\tag{4.8}
$$

Problem 15.5

質量$${m}$$の単一の調和振動子の自由度$${q}$$が以下の一般化ランジュバン方程式に従うとする。

$$
\begin{align*}
\ddot{q}&=-\omega^2q-\int_0^t{\rm d}\tau\dot{q}(\tau)\gamma(t-\tau)+f(t)
\end{align*}
$$

ここで$${\omega}$$が$${q}$$の振動数，$${\gamma(t):=\zeta(t)/m,\ f(t):=R(t)/m}$$，$${R(t)}$$はランダム力，$${\zeta(t)}$$は摩擦カーネルである。$${q(0)=0}$$とする。

a. 速度自己相関関数$${C_{vv}(t)}$$が以下の積分微分方程式に従うことを示せ。

$$
\begin{align*}
\frac{\rm d}{{\rm d}t}C_{vv}(t)&=-\int_{0}^t{\rm d}\tau K(t-\tau)C_{vv}(\tau)
\end{align*}
$$

ここで，$${K(t)=\omega^2+\gamma(t)}$$である。この方程式はヴォルテラ方程式と称される積分微分方程式の一種である。

b. 分子動力学シミュレーションから得られた速度自己相関関数を用いてメモリ関数と摩擦カーネルを抽出する数値アルゴリズムを考案せよ。ヴォルテラ方程式の逆問題解析が必要となることに注意せよ。アルゴリズムを実装する上で生じると予期される数値的困難を議論せよ。

c. 摩擦カーネルが$${\gamma(t)=\lambda A{\rm e}^{-\lambda t}}$$となる単純な連続モデルを考える。どの時間範囲においてこのモデルが物理的に崩壊すると予期されるか？また，その理由は？

d. c.の場合における速度自己相関関数に対するヴォルテラ方程式を解け。解におけるパラメータ$${A,\ \lambda}$$の影響を議論せよ。加えて，$${\omega\rightarrow 0}$$の極限を取ることで自由粒子の場合を調べよ。

e. 最後に，$${A,\ \lambda}$$を適用な値を代入し，得られた速度自己相関関数を時間ステップ$${\Delta t}$$で離散化して，b.で構築したアルゴリズムをテストせよ。指数関数的な摩擦カーネルをどの程度再現できるであろうか？また，離散化された$${C_{vv}(t)}$$に微小のランダムノイズを付加した場合の数値解のロバストネスはどの程度か？

$$
\begin{align*}
\frac{\rm d}{{\rm d}t}C_{vv}(t)&=\langle \dot{q}(0)\ddot{q}(t)\rangle\\
&=-\omega^2\langle \dot{q}(0)q(t)\rangle-\int_0^t{\rm d}\tau\langle \dot{q}(0)\dot{q}(\tau)\rangle\gamma(t-\tau)+\langle \dot{q}(0)f(t)\rangle\\
&=-\int_0^t{\rm d}\tau \langle \dot{q}(0)\dot{q}(\tau)\rangle(\omega^2+\gamma(t-\tau))\\
&=-\int_0^t{\rm d}\tau K(t-\tau)C_{vv}(\tau)
\end{align*}\tag{5.1}
$$

b. (5.1)式に両辺をラプラス変換すると，

$$
\begin{align*}
s\tilde{C}_{vv}(s)-C_{vv}(0)&=-\tilde{K}(s)\tilde{C}_{vv}(s)\\
\therefore \tilde{K}(s)&=\frac{C_{vv}(0)}{\tilde{C}_{vv}(s)}-s
\end{align*}\tag{5.2}
$$

それゆえ，数値計算で得られた$${C_{vv}(t)}$$をラプラス変換し，(5.2)式の$${\tilde{K}(s)}$$を逆ラプラス変換することで$${K(t)}$$が得られる。
実際の困難としては，ラプラス変換及び逆ラプラス変換を高精度に実行できるかが挙げられる。特に$${\tilde{K}(s)}$$には$${1/\tilde{C}_{vv}(s)}$$が含まれるため，$${\tilde{C}_{vv}(s)}$$の値が小さい部分が$${\tilde{K}(s)}$$に大きく影響してしまうのは厄介であることが懸念される。

c. 「物理的に崩壊」(break down phisically)の問われている意味が良く分からないため，略。。。

d. $${\tilde{K}(s)=\omega^2/s+\lambda A/(s+\lambda)}$$を(5.2)式に代入して，

$$
\begin{align*}
s\tilde{C}_{vv}(s)-C_{vv}(0)&=-\left(\frac{\omega^2}{s}+\frac{\lambda A}{s+\lambda}\right)\tilde{C}_{vv}(s)\\
\therefore \tilde{C}_{vv}(s)&=\frac{C_{vv}(0)}{s+\omega^2/s+\lambda A/(s+\lambda)}\\
&=C_{vv}(0)\frac{s(s+\lambda)}{s^3+\lambda s^2+(\omega^2+\lambda A)s+\omega^2\lambda}\\
\end{align*}\tag{5.3}
$$

$${s^3+\lambda s^2+(\omega^2+\lambda A)s+\omega^2\lambda}$$の根を$${p_i,\ i=1,2,3}$$とすると，

$$
\begin{align*}
\tilde{C}_{vv}(s)&=C_{vv}(0)\frac{s(s+\lambda)}{(s-p_1)(s-p_2)(s-p_3)}\\
\end{align*}\tag{5.4}
$$

重根がないよう$${A, \lambda, \omega}$$の値を選ぶとする。
$${p_i\neq0,-\lambda}$$より，(5.4)式は以下のように変形できる。

$$
\begin{align*}
\tilde{C}_{vv}(s)&=C_{vv}(0)\sum_{i=1}^3\frac{K_i}{(s-p_i)}\\
K_i&=\lim_{s\rightarrow p_i}(s-p_i)\tilde{C}_{vv}(s)\\
&=\frac{p_i^2+\lambda}{3p_i^2+2\lambda p_i+\omega^2+\lambda A}
\end{align*}\tag{5.5}
$$

(5.5)式の両辺を逆ラプラス変換することにより，

$$
\begin{align*}
C_{vv}(t)&=\sum_{i=1}^3\frac{p_i^2+\lambda p_i}{3p_i^2+2\lambda p_i+\omega^2+\lambda A}{\rm e}^{p_i t}\\
\end{align*}\tag{5.6}
$$

python3での(5.6)式の実装例を以下に示す。

# Import modules
import numpy as np
import sympy

# Parameters
omega = 1
A     = 0.0
Lamb  = 1
t     = np.linspace(0, 50, 501)

# Solve cubic equation using sympy
sympy.var("x")
s = sympy.solve(x ** 3 + Lamb * x ** 2 + (omega ** 2 + Lamb * A) * x + Lamb * omega ** 2)
s = np.array([complex(s[i]) for i in range(3)])

# Calculate coefficients
K = s ** 2 + Lamb * s
K /= 3 * s ** 2 + 2 * Lamb * s + omega **2 + Lamb * A
K = K.reshape((3, 1))

# Calculate velocity auto-correlation function
C_vv = np.array([np.exp(s[i] * t) for i in range(3)])
C_vv *= K
C_vv = np.sum(C_vv, axis = 0)
for a, b in zip(t, C_vv):
    print(f"{a},{b.real}")

$${\omega=1,\ A=1}$$に固定した場合の$${\lambda}$$に対する$${C_{vv}(t)}$$の様子を図5.1に示す。$${\lambda}$$が大きくなるほど，$${C_{vv}(t)}$$はより早く減衰し，また振動数も大きくなる。

$${\omega=1,\ \lambda=1}$$に固定した場合の$${A}$$に対する$${C_{vv}(t)}$$の様子を図5.2に示す。

$${\omega=0}$$の場合は，$${s^2+\lambda s+\lambda A}$$の根を$${p_i,\ i=4,5}$$とおくと，

$$
\begin{align*}
C_{vv}(t)&=\sum_{i=4}^5\frac{p_i+\lambda }{2p_i+\lambda}{\rm e}^{p_i t}\\
\end{align*}\tag{5.7}
$$

$${\lambda=1}$$に固定した場合の$${A}$$に対する$${C_{vv}(t)}$$の様子を図5.3に示す。

e. $${\omega=1,\ A=1,\ \lambda=1}$$の場合の$${\tilde{K}(s)}$$の数値解と解析解の比較を図5.4に示す。数値解では$${s}$$の値が大きい領域の情報が失われてしまっている。

Problem 15.6

Problem 15.4で取り扱った方程式に従う粒子の振動状態の密度と摩擦カーネルに以下の関係式が成立することを示せ。

$$
\begin{align*}
I(\omega)&=\frac{\omega^2\Re[\gamma(-{\rm i}\tilde{\omega})]}{[\omega^2-\tilde{\omega}^2-\omega\Im[\gamma(-{\rm i}\tilde{\omega})]]^2+[\omega\Re[\gamma(-{\rm i}\tilde{\omega})]]^2}
\end{align*}
$$

ここで，$${I(\omega)}$$は速度自己相関関数のフーリエ変換である。

$$
\begin{align*}
I(\omega)&=\frac{1}{2\pi}\int_{-\infty}^{\infty}{\rm d}t C_{vv}(t){\rm e}^{-{\rm i}\omega t}
\end{align*}
$$

一般的に，ランダム過程の自己相関関数とスペクトル密度の関係はウィーナー＝ヒンチンの定理として知られている。(15.2.17)を用いることにより，ランダム力の自己相関関数$${\lang R(0)R(t)\rang}$$に対応する調和浴のスペクトル密度を導出せよ。

$$
\begin{align*}
\lang R(0)R(t)\rang&=k_{\rm B}T\sum_{\alpha}\frac{g_{\alpha}^2}{m_{\alpha}\omega_{\alpha}^2}\cos\omega_{\alpha}t\\
&=k_{\rm B}T\zeta(t)
\end{align*}\tag{15.2.17}
$$

$${\langle\dot{q}^2\rangle C_{vv}(-t)=\langle\dot{q}(0)\dot{q}(-t)\rangle=\langle\dot{q}(t)\dot{q}(0)\rangle=\langle\dot{q}(0)\dot{q}(t)\rangle=\langle\dot{q}^2\rangle C_{vv}(t)}$$より，

$$
\begin{align*}
I(\omega)&=\frac{1}{2\pi}\int_{-\infty}^{\infty}{\rm d}t C_{vv}(t){\rm e}^{-{\rm i}\omega t}\\
&=\frac{1}{2\pi}\left\{\int_{0}^{\infty}{\rm d}t C_{vv}(t){\rm e}^{-{\rm i}\omega t}+\int_{-\infty}^{0}{\rm d}t C_{vv}(t){\rm e}^{-{\rm i}\omega t}\right\}\\
&=\frac{1}{2\pi}\left\{\int_{0}^{\infty}{\rm d}t C_{vv}(t){\rm e}^{-{\rm i}\omega t}-\int_{\infty}^{0}{\rm d}t C_{vv}(-t){\rm e}^{{\rm i}\omega t}\right\}\\
&=\frac{1}{2\pi}\left\{\int_{0}^{\infty}{\rm d}t C_{vv}(t){\rm e}^{-{\rm i}\omega t}+\int_{0}^{\infty}{\rm d}t C_{vv}(t){\rm e}^{{\rm i}\omega t}\right\}\\
&=\frac{1}{\pi}\int_{0}^{\infty}{\rm d}t C_{vv}(t)\cos\omega t\\
\end{align*}\tag{6.1}
$$

(6.1)式に(4.1)式で与えられる$${C_{vv}(t)}$$の表式を代入すると，

$$
\begin{align*}
I(\omega)&=\frac{1}{\pi}\int_{0}^{\infty}{\rm d}t {\rm e}^{-\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]t/2}\left[\cos\Omega t-\frac{\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]}{2\Omega}\sin\Omega t\right]\cos\omega t\\
&=\frac{1}{2\pi}\int_{0}^{\infty}{\rm d}t {\rm e}^{-\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]t/2}\left[\cos(\Omega-\omega)t+\cos(\Omega+\omega)t\right]\\
&\ \ \ -\frac{\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]}{4\pi \Omega}\int_{0}^{\infty}{\rm d}t {\rm e}^{-\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]t/2}\left[\sin(\Omega-\omega)t+\sin(\Omega+\omega)t\right]\\
&=\frac{\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]}{4\pi}\left\{\frac{1}{\frac{\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]^2}{4}+(\Omega-\omega)^2}+\frac{1}{\frac{\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]^2}{4}+(\Omega+\omega)^2}\right\}\\
&\ \ \ -\frac{\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]}{4\pi\Omega}\left\{\frac{\Omega-\omega}{\frac{\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]^2}{4}+(\Omega-\omega)^2}+\frac{\Omega+\omega}{\frac{\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]^2}{4}+(\Omega+\omega)^2}\right\}\\
&=\frac{\omega\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]}{4\pi\Omega}\left\{\frac{1}{\frac{\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]^2}{4}+(\Omega-\omega)^2}-\frac{1}{\frac{\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]^2}{4}+(\Omega+\omega)^2}\right\}\\
&=\frac{\omega^2\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]}{\pi}\frac{1}{\frac{\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]^2}{4}+(\Omega-\omega)^2}\frac{1}{\frac{\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]^2}{4}+(\Omega+\omega)^2}\\
&=\frac{\omega^2\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]}{\pi}\frac{1}{(\omega^2-\Omega^2)^2+\frac{\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]^2}{2}(\Omega^2+\omega^2)+\frac{\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]^4}{16}}\\
\end{align*}\tag{6.2}
$$

ここで，$${\Omega=\tilde{\omega}+\Im[\tilde{\gamma}(-{\rm i}\tilde{\omega})]/2}$$であることを思い出し，また$${\tilde{\gamma}}$$の2乗以降を無視すると，

$$
\begin{align*}
&I(\omega)\\
&\simeq\frac{1}{\pi}\frac{\omega^2\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})]}{(\omega^2-\tilde{\omega}^2-\tilde{\omega}\Im[\tilde{\gamma}(-{\rm i}\tilde{\omega})])^2+\frac{1}{2}[(\tilde{\omega}\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})])^2+(\omega\Re[\tilde{\gamma}(-{\rm i}\tilde{\omega})])^2]}\\
\end{align*}\tag{6.3}
$$

に帰着する。
（問題文の式は誤植？）

一方，$${\lang R(0)R(t)\rang}$$のスペクトル密度は，

$$
\begin{align*}
I_{RR}(\omega)&:=\frac{1}{2\pi}\int_{-\infty}^{\infty}{\rm d}t\lang R(0)R(t)\rang{\rm e}^{-{\rm i}\omega t}\\
&=\frac{1}{2\pi}\sum_{\alpha}\frac{g_{\alpha}^2}{m_{\alpha}\omega_{\alpha}^2}\int_{-\infty}^{\infty}{\rm d}t\cos\omega_{\alpha}t{\rm e}^{-{\rm i}\omega t}\\
&=\frac{1}{4\pi}\sum_{\alpha}\frac{g_{\alpha}^2}{m_{\alpha}\omega_{\alpha}^2}\int_{-\infty}^{\infty}{\rm d}t\left[{\rm e}^{{\rm i}\omega_{\alpha} t}+{\rm e}^{-{\rm i}\omega_{\alpha} t}\right]{\rm e}^{-{\rm i}\omega t}\\
&=\frac{1}{2}\sum_{\alpha}\frac{g_{\alpha}^2}{m_{\alpha}\omega_{\alpha}^2}\left[\delta(\omega_{\alpha}-\omega)+\delta(\omega_{\alpha}+\omega)\right]
\end{align*}\tag{6.4}
$$

Problem 15.7

ガウス型のランダム力を用いて調和振動子のランジュバン方程式を積分するプログラムを書け。質量$${m=1}$$，振動数$${\omega=1}$$，温度$${k_{\rm B}T=1}$$，摩擦係数$${\gamma=1}$$に設定し，15.5節の積分方法を用いよ。運動量と位置に関してカノニカル分布関数が再現されることを実証せよ。

python3による実装例を以下に示す。

import numpy as np
import matplotlib.pyplot as plt

# Parameters
m      = 1
omega  = 1
kbT    = 1
gamma  = 1
dt     = 0.01
q      = [np.random.normal(0, np.sqrt(kbT / (m * omega ** 2)))]
v      = [np.random.normal(0, np.sqrt(kbT / m))]
n_step = 100000000
sigma  = np.sqrt(2 * kbT * gamma / m)

# Define functions
def Force(q):
    return  - (omega ** 2) * q / m
    
def RandomDeplacement(q, v, xi, theta):
    return 0.5 * (dt ** 2) * (Force(q) - gamma * v) + sigma * (dt ** 1.5) * 0.5 * (xi + theta / np.sqrt(3))

def Density(x_max, variable = "q"):
    sigma2 = kbT / m 
    if variable == "q":
        sigma2 /= omega ** 2
    
    else:
        coeff = np.sqrt(0.5 * m / np.pi / kbT)
    x = np.linspace(-x_max, x_max, 101)
    
    return  x, np.exp(-0.5 * x ** 2 / sigma2) / np.sqrt(2 * np.pi * sigma2)

# Integrate the equation
for _ in range(n_step):
    xi, theta = np.random.normal(0, 1, 2)
    A = RandomDeplacement(q[-1], v[-1], xi, theta)
    q.append(q[-1] + dt * v[-1] + A)
    v.append((1 - dt * gamma) * v[-1] + 0.5 * dt * (Force(q[-2]) + Force(q[-1])) + np.sqrt(dt) * sigma * xi - gamma * A)
    
q = np.array(q)
v = np.array(v)

plt.hist(q , density = True, bins = 51, label = "numerical")

plt.plot(*Density(q.max(), variable = "q"), label = "analytical")
plt.xlabel("q")
plt.ylabel("f(q)")
plt.legend()
plt.savefig("f(q).png")
plt.figure()

plt.hist(v , density = True, bins = 51, label = "numerical")
plt.plot(*Density(q.max(), variable = "v"), label = "analytical")
plt.xlabel("v")
plt.ylabel("f(v)")
plt.legend()
plt.savefig("f(v).png")
plt.figure()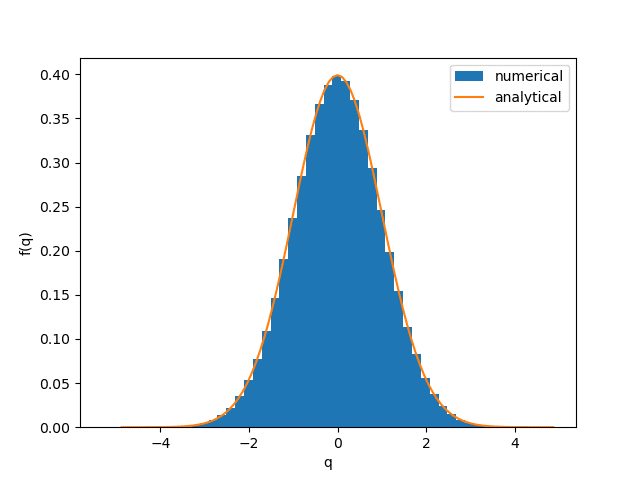

Problem 15.8

8.10節で扱った断熱的自由エネルギー動力学によるアプローチを考える。

a. $${n}$$個の座標が$${T_q}$$の熱浴，残りの$${3N-n}$$個の座標が$${T}$$の熱浴と接合している場合に対して，ランジュバン方程式を再定式化せよ。

b. (8.10.21)式で与えられるポテンシャルに対してランジュバン方程式を積分し，(8.10.22)式で与えられる自由エネルギープロファイルの解析解を再現できることを確かめよ。

$$
\begin{align*}
U(x,y)&=D_0\left(x^2-a^2\right)^2+\frac{1}{2}ky^2+\lambda xy
\end{align*}\tag{~~8.10.21~~}
$$

$$
\begin{align*}
A(x)&=D_0\left(x^2-a^2\right)^2+\frac{\lambda^2}{2k}x^2
\end{align*}\tag{8.10.22}
$$

$$
\begin{align*}
\mu_i\ddot{q}_i(t)&=F(q_1(t),\cdots,q_{3N}(t))-\gamma_i \mu_i\dot{q}_i(t)+\sqrt{2k_{\rm B}T_q\gamma_i\mu_i}\eta_i(t)\\
i&=1,\cdots,n\\\\
\mu_j\ddot{q}_j(t)&=F(q_1(t),\cdots,q_{3N}(t))-\gamma_j \mu_j\dot{q}_j(t)+\sqrt{2k_{\rm B}T\gamma_j\mu_j}\eta_j(t)\\
j&=n+1,\cdots,3N\\
\end{align*}\tag{8.1}
$$

b. python3による実装例を以下に示す。

import numpy as np
import matplotlib.pyplot as plt
import sys

np.random.seed(seed = 2024)

# Parameters
n_step    = 1000000
weights   = np.array([300, 1])
D0        = 5
a         = 1
k         = 1
lam       = 2.878
kbT       = np.array([10, 1])
gamma     = 1
coords    = np.zeros((n_step + 1, 2))
coords[0] = np.array([np.sqrt(pow(a, 2) + 0.25 * pow(lam, 2) / D0 / k), 0])
vels      = np.zeros((n_step + 1, 2))
vels[0]   = np.random.normal(0, np.sqrt(kbT / weights))
dt        = 0.05
sigma     = np.sqrt(2 * kbT * gamma / weights)

# Define functions
def potEnergy(r):
    return D0 * pow(pow(r[0], 2) - pow(a, 2), 2) + 0.5 * k * pow(r[1], 2) + lam * r[0] * r[1]
 
def Force(r):
    f_x = - 4 * D0 * r[0] * (pow(r[0], 2) - pow(a, 2)) - lam * r[1]
    f_y = - k * r[1] - lam * r[0]
    return np.array([f_x, f_y]) / weights

def RandomDisplacement(r, v, xi, theta):
    return 0.5 * pow(dt, 2) * (Force(r) - gamma * v) + sigma * pow(dt, 1.5) * 0.5 * (xi + theta / np.sqrt(3))

def AnalyticalFE(x):
    FE = D0 *  pow(pow(x, 2) - pow(a, 2), 2) - 0.5 * pow(lam * x, 2) / k
    FE -= np.min(FE)
    return FE
    
def analyzeFreeEnergyProfile(coord):
    # Analyze free energy profile numerically and compare the analysical result
    grids = np.linspace(min(coord), max(coord), 101)
    hist = np.histogram(coord, bins = grids)[0]
    grids2 = np.zeros(100)
    for i in range(len(grids) - 1):
        grids2[i] = 0.5 * (grids[i] + grids[i + 1])

    fes_n = -kbT[0] * np.log(hist)
    fes_n -= min(fes_n)

    fes_a = AnalyticalFE(grids2)
    fes_a -= min(fes_a)
    for x, f1, f2 in zip(grids2, fes_n, fes_a):
        print(x, f1, f2)
   
# Integrate the equation
for i in range(n_step):
    xi = np.random.normal(0, 1, 2)
    theta = np.random.normal(0, 1, 2)
    A = RandomDisplacement(coords[i], vels[i], xi, theta)
    coords[i + 1] = coords[i] + dt * vels[i] + A
    vels[i + 1] = (1 - dt * gamma) * vels[i] + 0.5 * dt * (Force(coords[i]) + Force(coords[i + 1])) + np.sqrt(dt) * sigma * xi - gamma * A
    sys.stdout.write(f"\r Progress: {i / n_step:.0%}")
    sys.stdout.flush()
    #if (i % (n_step // 10) == 0) and (i > 0):
    #    print("\n")
    #    analyzeFreeEnergyProfile(coords[:,0][:i])
    #    print("\n")
print("\n")
analyzeFreeEnergyProfile(coords[:,0][:i])

Problem 15.9

a. 対象となる部分系が位置$${x}$$，運動量$${p}$$，質量$${\mu}$$，振動数$${\omega}$$の１次元調和振動子である場合を考える。力定数行列$${{\rm i}\boldsymbol\Omega}$$，メモリーカーネル$${\mathbf{K}(t)}$$の表式を導出せよ。
$${{\rm i}\boldsymbol\Omega}$$は$${\mathbf{A}:=\begin{bmatrix}x&p\end{bmatrix}^{\rm T}}$$に対して，

$$
\begin{align*}
{\rm i}\boldsymbol\Omega&=\left\lang{\rm i}\mathcal{L}\mathbf{A}\mathbf{A}^{\dagger}\right\rang\left\lang\mathbf{A}\mathbf{A}^{\dagger}\right\rang^{-1}
\end{align*}
$$

と定義される。ここで，$${{\rm i}\mathcal{L}}$$はリウヴィル演算子，$${\lang\cdots\rang}$$はカノニカルアンサンブル平均である。
$${\mathbf{K}(t)}$$は一般化力$${{\rm i}\mathcal{L}\mathbf{A}}$$の$${\mathbf{A}}$$と直交する成分$${\mathbf{F}(t):=\mathcal{Q}{\rm i}\mathcal{L}\mathbf{A}}$$を用いて，

$$
\begin{align*}
\mathbf{K}(t)&:=\left\lang\mathbf{F}(t)\mathbf{F}^{\dagger}(0)\right\rang\left\lang\mathbf{A}\mathbf{A}^{\dagger}\right\rang^{-1}\\
&=\left\lang{\rm e}^{\mathcal{Q}{\rm i}\mathcal{L}t}\mathbf{F}(0)\mathbf{F}^{\dagger}(0)\right\rang\left\lang\mathbf{A}\mathbf{A}^{\dagger}\right\rang^{-1}\\
&=\left\lang{\mathbf{F}^{\dagger}(0)\rm e}^{\mathcal{Q}{\rm i}\mathcal{L}t}\mathbf{F}(0)\right\rang\left\lang\mathbf{A}\mathbf{A}^{\dagger}\right\rang^{-1}\\
\mathbf{F}(t)&={\rm e}^{\mathcal{Q}{\rm i}\mathcal{L}t}\mathcal{Q}{\rm i}\mathcal{L}\mathbf{A}(0)
\end{align*}
$$

と定義される。
さらに，$${\mathbf{F}}$$のうち$${0}$$にならない項を$${\delta f}$$と表記することにする。このとき，摩擦カーネル$${\zeta(t)}$$は以下の表式に帰着する。

$$
\begin{align*}
\frac{\zeta(t)}{\mu}&=\frac{\left\lang\delta f{\rm e}^{\mathcal{Q}{\rm i}\mathcal{L}t}\delta f\right\rang}{\left\lang p^2\right\rang}
\end{align*}
$$

$$
\begin{align*}
\frac{\phi(t)}{\mu}&:=\frac{\left\lang\delta f{\rm e}^{{\rm i}\mathcal{L}t}\delta f\right\rang}{\left\lang p^2\right\rang}
\end{align*}
$$

としたとき，$${\zeta(t)}$$と$${\phi(t)}$$のラプラス変換に以下の関係式が成立する（Berne et al. (1990) ）ことを示せ。

$$
\begin{align*}
\frac{\tilde{\zeta}(s)}{\mu}&=\frac{\left[\tilde{\phi}(s)/\mu\right]}{1-\left\{\left[s/(s^2+\tilde{\omega}^2)\right]\left[\tilde{\phi}(s)/\mu\right]\right\}}
\end{align*}
$$

$$
\begin{align*}
\left\lang\mathbf{A}\mathbf{A}^{\dagger}\right\rang&=\left\lang\begin{bmatrix}x^2&xp\\px&p^2\end{bmatrix}\right\rang\\
&=\begin{bmatrix}\left\lang x^2\right\rang&0\\0&\left\lang p^2\right\rang\end{bmatrix}\\
\therefore \left\lang\mathbf{A}\mathbf{A}^{\dagger}\right\rang^{-1}&=\begin{bmatrix}1/\left\lang x^2\right\rang&0\\0&1/\left\lang p^2\right\rang\end{bmatrix}\\
\end{align*}\tag{9.1}
$$

また，

$$
\begin{align*}
{\rm i}\mathcal{L}&=\frac{\partial \mathcal{H}}{\partial p}\frac{\partial}{\partial x}-\frac{\partial \mathcal{H}}{\partial x}\frac{\partial}{\partial p}\\
&=\frac{p}{\mu}\frac{\partial}{\partial x}-\frac{\partial \mathcal{H}}{\partial x}\frac{\partial}{\partial p}
\end{align*}\tag{9.2}
$$

より，

$$
\begin{align*}
\left\lang{\rm i}\mathcal{L}\mathbf{A}\mathbf{A}^{\dagger}\right\rang&=\left\lang\begin{bmatrix}xp/\mu&p^2/\mu\\-x\frac{\partial\mathcal{H}}{\partial x}&-p\frac{\partial\mathcal{H}}{\partial x}\end{bmatrix}\right\rang\\
&=\begin{bmatrix}0&\left\lang p^2\right\rang/\mu\\-\left\lang x\frac{\partial\mathcal{H}}{\partial x}\right\rang&0\end{bmatrix}\\
&=\begin{bmatrix}0&\left\lang p^2\right\rang/\mu\\-1/\beta&0\end{bmatrix}\\
\end{align*}\tag{9.3}
$$

$$
\begin{align*}
\therefore{\rm i}\boldsymbol\Omega&=\left\lang{\rm i}\mathcal{L}\mathbf{A}\mathbf{A}^{\dagger}\right\rang\left\lang\mathbf{A}\mathbf{A}^{\dagger}\right\rang^{-1}\\
&=\begin{bmatrix}0&1/\mu\\-\frac{1}{\beta\left\lang x^2\right\rang}&0\end{bmatrix}\\
&=\begin{bmatrix}0&1/\mu\\-\mu\tilde{\omega}^2&0\end{bmatrix}\\
\tilde{\omega}^2&:=\frac{1}{\beta\mu\left\lang x^2\right\rang}
\end{align*}\tag{9.4}
$$

$$
\begin{align*}
\mathbf{F}(t)&=\mathcal{Q}{\rm i}\mathcal{L}\mathbf{A}(t)\\
&={\rm i}\mathcal{L}\mathbf{A}(t)-{\rm i}\boldsymbol\Omega\mathbf{A}(t)\\
&=\begin{bmatrix}0\\-\frac{\partial\mathcal{H}}{\partial x}+\mu\tilde{\omega}^2x(t)\end{bmatrix}\\
&=\begin{bmatrix}0\\\dot{p}(t)+\mu\tilde{\omega}^2x(t)\end{bmatrix}\\
\end{align*}\tag{9.5}
$$

$$
\begin{align*}
\therefore \mathbf{K}(t)&=\begin{bmatrix}0&0\\0&\left\lang\delta f{\rm e}^{\mathcal{Q}{\rm i}\mathcal{L}t}\delta f\right\rang/\left\lang p^2\right\rang\end{bmatrix}\\
&=\begin{bmatrix}0&0\\0&\zeta(t)/\mu\end{bmatrix}
\end{align*}\tag{9.6}
$$

b. $${\boldsymbol\Phi(t):=\lang{\rm e}^{{\rm i}\mathcal{L}t}\mathbf{F}(0)\mathbf{F}^{\dagger}(0)\rang\lang\mathbf{A}\mathbf{A}^{\dagger}\rang^{-1}}$$とおくと，参考文献2, 3によると$${\boldsymbol\Phi(t)}$$と$${\mathbf{K}(t)}$$のラプラス変換には以下の関係式が成立する。

$$
\begin{align*}
\tilde{\mathbf{K}}(s)&=\tilde{\boldsymbol\Phi}(s)\left[\mathbf{I}-\left(s\mathbf{I}-{\rm i}\boldsymbol\Omega\right)^{-1}\tilde{\boldsymbol\Phi}(s)\right]^{-1}
\end{align*}\tag{9.7}
$$

a.で得られた表式を(9.7)式に代入すると，

$$
\begin{align*}
\left(s\mathbf{I}-{\rm i}\boldsymbol\Omega\right)^{-1}&=\begin{bmatrix}s&-1/\mu\\\mu\tilde{\omega}^2&s\end{bmatrix}^{-1}\\
&=\frac{1}{s^2+\tilde{\omega}^2}\begin{bmatrix}s&1/\mu\\-\mu\tilde{\omega}^2&s\end{bmatrix}
\end{align*}\tag{9.8}
$$

$$
\begin{align*}
\left(s\mathbf{I}-{\rm i}\boldsymbol\Omega\right)^{-1}\tilde{\boldsymbol\Phi}(s)&=\frac{1}{s^2+\tilde{\omega}^2}\begin{bmatrix}s&1/\mu\\-\mu\tilde{\omega}^2&s\end{bmatrix}\tilde{\boldsymbol\Phi}(s)\\
&=\frac{1}{s^2+\tilde{\omega}^2}\begin{bmatrix}s&1/\mu\\-\mu\tilde{\omega}^2&s\end{bmatrix}\begin{bmatrix}0&0\\0&\tilde{\phi}(s)/\mu\end{bmatrix}\\
&=\frac{1}{s^2+\tilde{\omega}^2}\begin{bmatrix}s&\tilde{\phi}(s)/\mu^2\\0&s\tilde{\phi}(s)/\mu\end{bmatrix}\\
\end{align*}\tag{9.9}
$$

$$
\begin{align*}
&\left[\mathbf{I}-\left(s\mathbf{I}-{\rm i}\boldsymbol\Omega\right)^{-1}\tilde{\boldsymbol\Phi}(s)\right]^{-1}\\
&=\begin{bmatrix}1-\frac{s}{s^2+\tilde{\omega}^2}&-\tilde{\phi}(s)/\mu^2\\0&1-\frac{s}{s^2+\tilde{\omega}^2}\frac{\tilde{\phi}(s)}{\mu}\end{bmatrix}^{-1}\\
&=\frac{1}{\left(1-\frac{s}{s^2+\tilde{\omega}^2}\right)\left(1-\frac{s}{s^2+\tilde{\omega}^2}\frac{\tilde{\phi}(s)}{\mu}\right)}\begin{bmatrix}1-\frac{s}{s^2+\tilde{\omega}^2}\frac{\tilde{\phi}(s)}{\mu}&\tilde{\phi}(s)/\mu^2\\0&1-\frac{s}{s^2+\tilde{\omega}^2}\end{bmatrix}\\
\end{align*}\tag{9.10}
$$

$$
\begin{align*}
\therefore \frac{\tilde{\zeta}(s)}{\mu}
&=\frac{\left(1-\frac{s}{s^2+\tilde{\omega}^2}\right)\frac{\tilde{\phi}(s)}{\mu}}{\left(1-\frac{s}{s^2+\tilde{\omega}^2}\right)\left(1-\frac{s}{s^2+\tilde{\omega}^2}\frac{\tilde{\phi}(s)}{\mu}\right)}\\
&=\frac{\frac{\tilde{\phi}(s)}{\mu}}{1-\frac{s}{s^2+\tilde{\omega}^2}\frac{\tilde{\phi}(s)}{\mu}}\\
\end{align*}\tag{9.11}
$$

Problem 15.10

極低密度の溶質分子$${\rm A}$$と溶媒分子$${\rm B}$$からなる溶液を考える。溶質分子数を$${N_{\rm A}}$$と表記し，各位置座標を$${\mathbf{r}_1(t),\cdots,\mathbf{r}_{N_{\rm A}}(t)}$$とする。位置$${\mathbf{r}}$$における溶質の密度を$${c(\mathbf{r},t)}$$とおく。

$$
\begin{align*}
c(\mathbf{r},t)&=\sum_{i=1}^{N_{\rm A}}\delta(\mathbf{r}-\mathbf{r}_i(t))
\end{align*}
$$

a. 溶液が長さ$${L}$$の立方体にあると仮定した場合，$${c(\mathbf{r},t)}$$の空間フーリエ変換$${\tilde{c}_{\mathbf{k}}(t)}$$が

$$
\begin{align*}
\tilde{c}_{\mathbf{k}}(t)&=\sum_{i=1}^{N_{\rm A}}{\rm e}^{-{\rm i}\mathbf{k}\cdot\mathbf{r}_i(t)}
\end{align*}
$$

となることを示せ。
ここで，$${\mathbf{k}=2\pi\mathbf{n}/L}$$，$${\mathbf{n}}$$は整数ベクトルである。

b. Mori–Zwanzig理論を用いて$${\tilde{c}_{\mathbf{k}}(t)}$$に対する一般化ランジュバン方程式を導出し，方程式に現れる全ての項の明示的な表式を与えよ。

c. ここで，以下の相関関数を考える。

$$
\begin{align*}
C(\mathbf{k},t)&=\frac{\left\lang\tilde{c}_{-\mathbf{k}}(0)\tilde{c}_{\mathbf{k}}(t)\right\rang}{\left\lang\tilde{c}_{-\mathbf{k}}\tilde{c}_{\mathbf{k}}\right\rang}
\end{align*}
$$

一般化ランジュバン方程式を起点に$${C(\mathbf{k},t)}$$が満たす積分微分方程式を導出せよ。

d. メモリカーネルが$${\mathbf{k}}$$に対して少なくとも二次以上であることを示せ。

e. $${|\mathbf{k}|\rightarrow\infty}$$で$${\exp(\mathcal{Q}{\rm i}\mathcal{L}t)\rightarrow\exp({\rm i}\mathcal{L}t)}$$を示せ。

f. メモリカーネルが時間に対して速やかに減衰すると仮定する。この極限において，相関関数は以下の形式の方程式を満たすことを示せ。

$$
\begin{align*}
\frac{\partial}{\partial t}C(\mathbf{k},t)&=-\mathbf{k}\cdot\mathbf{D}\cdot\mathbf{k} C(\mathbf{k},t)
\end{align*}
$$

ここで，$${\mathbf{D}}$$は拡散テンソルである。速度自己相関関数を用いた$${\mathbf{D}}$$の表式を与えよ。

$$
\begin{align*}
\tilde{c}_{\mathbf{k}}(t)&=\int_{D(L^3)}{\rm d}\mathbf{r}{\rm e}^{-{\rm i}
\mathbf{k}\cdot\mathbf{r}}c(\mathbf{r},t)\\
&=\sum_{i=1}^{N_{\rm A}}\int_{D(L^3)}{\rm d}\mathbf{r}{\rm e}^{-{\rm i}
\mathbf{k}\cdot\mathbf{r}}\delta(\mathbf{r}-\mathbf{r}_i(t))\\
&=\sum_{i=1}^{N_{\rm A}}{\rm e}^{-{\rm i}\mathbf{k}\cdot\mathbf{r}_i(t)}
\end{align*}\tag{10.1}
$$

$${c(\mathbf{r},t)}$$に周期境界条件$${c(\mathbf{r}+L\mathbf{n},t)=c(\mathbf{r},t)}$$を課すことにより，$${\mathbf{k}=2\pi\mathbf{n}/L}$$となる。

b. 溶質分子の質量を$${m}$$，運動量を$${\mathbf{p}_i}$$とし，$${J_{\mathbf{k}}(t)}$$を(10.2)式で定義する。

$$
\begin{align*}
J_{\mathbf{k}}(t)&:=\frac{1}{m}\sum_{i=1}^{N_{\rm A}}\hat{\mathbf{k}}\cdot\mathbf{p}_i(t){\rm e}^{-{\rm i}\mathbf{k}\cdot\mathbf{r}_i(t)}\\
\hat{\mathbf{k}}&:=\frac{\mathbf{k}}{|\mathbf{k}|}=:\frac{\mathbf{k}}{k}
\end{align*}\tag{10.2}
$$

$${J_{\mathbf{k}}(t)}$$と$${\dot{\tilde{c}}_{\mathbf{k}}(t)}$$には(10.3)式の関係が成立する。

$$
\begin{align*}
\dot{\tilde{c}}_{\mathbf{k}}(t)&:=\sum_{i=1}^{N_{\rm A}}\left(-{\rm i}\mathbf{k}\cdot\dot{\mathbf{r}}_i(t)\right){\rm e}^{-{\rm i}\mathbf{k}\cdot\mathbf{r}_i(t)}\\
&=-{\rm i}\frac{k}{m}\sum_{i=1}^{N_{\rm A}}\hat{\mathbf{k}}\cdot\mathbf{p}_i(t){\rm e}^{-{\rm i}\mathbf{k}\cdot\mathbf{r}_i(t)}\\
&=-{\rm i}kJ_{\mathbf{k}}(t)
\end{align*}\tag{10.3}
$$

力学変数ベクトル$${\mathbf{A}}$$を$${\mathbf{A}=\begin{bmatrix}\tilde{c}_{\mathbf{k}}(t)&J_{\mathbf{k}}(t)\end{bmatrix}^{\rm T}}$$に選んだ場合，

$$
\begin{align*}
\left\lang\mathbf{A}\mathbf{A}^{\dagger}\right\rang&=\begin{bmatrix}\left\lang\tilde{c}_{\mathbf{k}}\tilde{c}_{\mathbf{k}}^*\right\rang&\left\lang\tilde{c}_{\mathbf{k}}J_{\mathbf{k}}^*\right\rang\\
\left\lang J_{\mathbf{k}}\tilde{c}_{\mathbf{k}}^*\right\rang
& \left\lang J_{\mathbf{k}}J_{\mathbf{k}}^*\right\rang\end{bmatrix}\\
&=\begin{bmatrix}\left\lang\tilde{c}_{\mathbf{k}}\tilde{c}_{-\mathbf{k}}\right\rang&\left\lang\tilde{c}_{\mathbf{k}}J_{\mathbf{k}}^*\right\rang\\
\left\lang J_{\mathbf{k}}\tilde{c}_{-\mathbf{k}}\right\rang
& \left\lang J_{\mathbf{k}}J_{\mathbf{k}}^*\right\rang\end{bmatrix}\\
&=N_{\rm A}\begin{bmatrix}1&0\\
0
& \frac{k_{\rm B}T}{m}\end{bmatrix}\\
\end{align*}\tag{10.4}
$$

$$
\begin{align*}
\left\lang{\rm i}\mathcal{L}\mathbf{A}\mathbf{A}^{\dagger}\right\rang&=\left\lang\dot{\mathbf{A}}\mathbf{A}^{\dagger}\right\rang\\
&=\begin{bmatrix}\left\lang\dot{\tilde{c}}_{\mathbf{k}}\tilde{c}_{-\mathbf{k}}\right\rang&\left\lang\dot{\tilde{c}}_{\mathbf{k}}J_{\mathbf{k}}^*\right\rang\\
\left\lang \dot{J}_{\mathbf{k}}\tilde{c}_{-\mathbf{k}}\right\rang
& \left\lang \dot{J}_{\mathbf{k}}J_{\mathbf{k}}^*\right\rang\end{bmatrix}\\
&=\begin{bmatrix}-{\rm i}k\left\lang J_{\mathbf{k}}\tilde{c}_{-\mathbf{k}}\right\rang&-{\rm i}k\left\lang J_{\mathbf{k}}J_{\mathbf{k}}^*\right\rang\\
\left\lang \dot{J}_{\mathbf{k}}\tilde{c}_{-\mathbf{k}}\right\rang
& \left\lang \dot{J}_{\mathbf{k}}J_{\mathbf{k}}^*\right\rang\end{bmatrix}\\
&=\frac{-{\rm i}kN_{\rm A}k_{\rm B}T}{m}\begin{bmatrix}0&1\\
1& 0\end{bmatrix}\\
\end{align*}\tag{10.5}
$$

$$
\begin{align*}
\mathbf{F}(t)&=\mathcal{Q}{\rm i}\mathcal{L}\mathbf{A}(t)\\
&={\rm i}\mathcal{L}\mathbf{A}(t)-\mathcal{P}{\rm i}\mathcal{L}\mathbf{A}(t)\\
&=\dot{\mathbf{A}}(t)-{\rm i}\boldsymbol\Omega\mathbf{A}(t)\\
&=\begin{bmatrix}0\\\dot{J}_{\mathbf{k}}(t)+\frac{{\rm i}kk_{\rm B}T}{m}\tilde{c}_{\mathbf{k}}(t)\end{bmatrix}\\
&=:\begin{bmatrix}0\\\delta f_{\mathbf{k}}(t)\end{bmatrix}\\
\end{align*}\tag{10.7}
$$

$$
\begin{align*}
\mathbf{K}(t)&=\left\lang \mathbf{F}(t)\mathbf{F}^{\dagger}(0)\right\rang\left\lang \mathbf{A}\mathbf{A}^{\dagger}\right\rang^{-1}\\
&=\frac{m}{N_{\rm A}k_{\rm B}T}\begin{bmatrix}0&0\\0&\left\lang\delta f_{\mathbf{k}}{\rm e}^{\mathcal{Q}{\rm i}\mathcal{L}t}\delta f_{\mathbf{k}}^*\right\rang\end{bmatrix}\\
\end{align*}\tag{10.8}
$$

(10.6)-(10.8)式を一般化ランジュバン方程式に代入すると(10.9)式に帰着する。

$$
\begin{align*}
\ddot{\tilde{c}}_{\mathbf{k}}(t)&=-\frac{k^2k_{\rm B}T}{m}\tilde{c}_{\mathbf{k}}(t)-\frac{m}{N_{\rm A}k_{\rm B}T}\int_0^t{\rm d}\tau\left\lang\delta f_{\mathbf{k}}{\rm e}^{\mathcal{Q}{\rm i}\mathcal{L}\tau}\delta f_{\mathbf{k}}^*\right\rang\dot{\tilde{c}}_{\mathbf{k}}(t-\tau)\\
&\ \ \ \ \ \ -{\rm i}k\delta f_{\mathbf{k}}(t)
\end{align*}\tag{10.9}
$$

c. b. の解法内容に自信なく，適当な参考書も見当たらなかったため，以降の問題解答を一旦放棄。。。解法を思いついたら更新します。。。

参考文献

Mark E. Tuckerman, Statistical Mechanics: Theory and Molecular Simulation (Oxford Graduate Texts)
B. J. Berne, et. al., J. Chem. Phys. 93 (7), 1 October 1990
B. J. Berne and R. Pecora, Dynamic Light Scattering (Wiley-Interscience, New York, 1976)

この記事が気に入ったらサポートをしてみませんか？