u-series

生体分子シミュレーションでは，ほとんどの場合，Amber系統もしくはそれと同等な関数形が原子間相互作用を表現するために使用されます（関数と関数内で使用されるパラメータはまとめて力場関数と称されます）。

①式の最後はクーロン相互作用項であり，原子間距離に反比例します。
このクーロン相互作用を如何に精度を落とさずに効率的に計算するかがシミュレーション上の大きな課題の一つになります。
Gromacs，Amber，NAMDといった多くのシミュレーションパッケージでは，クーロン相互作用項はEwald法ベースのParticle Mesh Ewald（PME）やParticle Particle Particle Mesh（PPPM） Ewaldが実装されており，Ewald法ベースの手法がデファクトスタンダードになっています。
一方，最近になってMD計算エンジンの一つであるDesmondの開発元のD. E. Shaw ResearchがEwald法とは異なる数学的手法に基づくu-seriesを発表しました（実際には論文公開のずっと前からDesmondにはu-seriesが実装されていたみたいです）。
本記事では，u-seriesの数学的な性質やEwald法と比較した際の優れた点等を解説します。

Ewald法

u-seriesの話の前にEwald法を簡単に振り返っておきます。
Ewald法では，1/rを誤差関数と相補誤差関数を用いて分解することを考えます。

②式右辺の第１項（near term）は元の1/rよりも早く0に収束する性質を持ちますので，より小さいカットオフ長を適用できます。
一方，②式右辺の第２項（far term）は実数空間では0への収束性が悪いですが，フーリエ変換すると

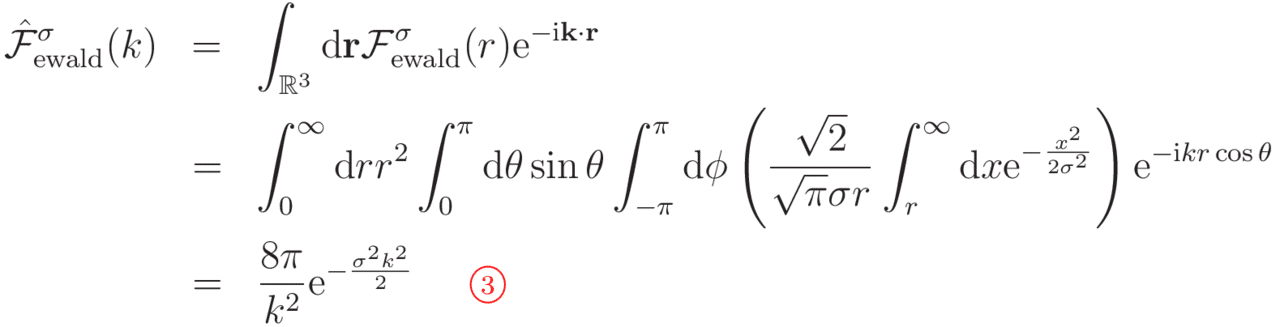
となり，波数空間では収束が速いことが分かります。
そのため，near termを実空間，far termを波数空間でそれぞれカットオフを設けて評価することにより，効率よくクーロン相互作用を計算することが可能になります。

カットオフ長r_cでのエネルギーや原子間力の不連続を避けるため，例えば以下のようなswitching関数を用いてnear termを評価することを考えます。

switching関数導入の関係で，r_c - λからnear termが実質的に0に収束するまでの区間で厳密解からの誤差が生じることになります。

Bilateral Series Approximation

u-seriesは，Bilateral Series Approximation(BSA)を出発点に1/rを分解します。
1/rに対するガウス関数を用いたbilateral series approximationは式⑤になります。

式⑤右辺の展開項はjが小さくなればなるほど0への収束が早くなるため，near termとfar termを

と定義することにします。
式⑥による1/rの分解は既に近似式になっていますし，Ewald法と比較してnear termの収束性が極端に良くなっているわけでもありません。
u-seriesでは，式⑥に若干の修正を施すことにより，望ましい性質を持つ関数に変換します。

u-series

u-seriesでは式⑥を出発点として，near termとfar termを

と定義します。
すると，near termとfar termの合計値が

となるため，r < r_cに関しては厳密に1/rを計算していることになります。
σの値はr = r_cでnear termとfar termの合計値が連続となるように選ばれます。

Ewald法と異なり，Switching関数の導入が不要な定式化となっています。

微分に対する連続性

エネルギーのみを評価すればよいモンテカルロ法の場合は⑦，⑧式で良いのですが，原子間力も評価する必要があるMD（Molecular Dynamics，分子動力学）計算では1/rの微分に対してもr = r_cで連続であることが望ましいです。
そのため，⑧式のFar partのうち最も収束が早いj = 0項の係数を変更することを考えます。

⑪，⑫式はσの値に関わらずr = r_cで連続となります。
更に⑬式がr = r_cで連続となるようにσを選ぶことで目的の関数を得ることができます。

同様の考え方で更に高階の微分についてもr = r_cで連続となるようにすることも可能です。

波数空間でのfar termの評価

⑧式にあるfar termは実空間での収束性が良くないため，波数空間で静電エネルギーを評価することを考えます。
周期境界条件を満たす電荷分布ρが存在する状況を想定して，⑭式にあるようにρのフーリエ級数展開を用います。

ここで，Vは単位胞の体積，Ωは単位胞内を積分範囲とすることを意味します。
このρによる静電ポテンシャル，及び単位胞あたりの静電エネルギーにおけるfar termの寄与を計算していきます。
まずは静電ポテンシャルのフーリエ展開係数を考えます。

積分が複雑になってきたため，式⑮の青い部分に着目して計算を続けます。

⑯式を⑮式に代入すると，

となります。これより，静電ポテンシャルは

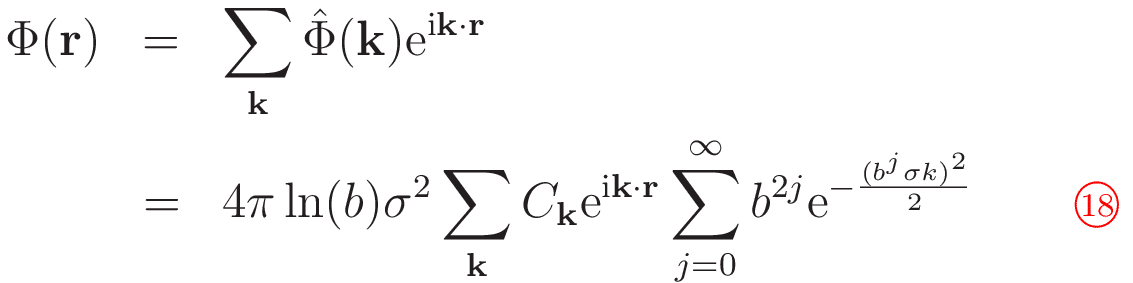
となります。
単位胞あたりの静電エネルギーは，self-energy項を取り除く前の表式が⑲式のようになります。

⑲式を用いて，jに関する和をN-1で打ち切った時の相対誤差を評価することができます。

base parameter "b"の精度と計算コストの関係

⑤式のBSAはb→1に従って，1/rに収束します。また，BSAの1/rに対する誤差上限は大よそ

となります。そのため，計算精度のみを考えたらbはなるべく小さい値にするべきです。
一方，⑳式にあるようにbを小さくするほど，far termの相対誤差を小さくするために必要となるNは大きくなります。また，関数の性質として，bを小さくするとσも併せて小さくしなければいけないことが挙げられます。
そのため，計算精度とコストのバランスを鑑みてbの値を決める必要があります。参考文献1によると，PME法と同等の計算精度をu-seriesで確保した場合，far termの計算コストはPME法の1/2程度で済むことが実証されています。これもu-seriesのメリットの一つです。

参考文献

1. J. Chem. Phys. 152, 084113 (2020)
2. Mark Tuckerman, Statistical Mechanics: Theory and Molecular Simulation (Oxford Graduate Texts)