
Statistical Mechanics: Theory and Molecular Simulation Chapter 8 - Free energy calculations
Statistical Mechanics: Theory and Molecular SimulationはMark Tuckermanによって著された分子シミュレーションに関連した熱・統計物理学,及び量子力学の参考書になります。
現時点では(恐らく)和訳がないこともあり,日本での知名度はあまりないような気がしますが,被引用数が1400を超えていることを考えると海外では高く認知されている参考書みたいです。
https://scholar.google.com/citations?user=w_7furwAAAAJ&hl=ja
本記事では,Chapter 8(Free energy calculations)の章末問題の和訳とその解答例を紹介します。解答例に間違いが見受けられた場合はお知らせいただけると助かります。
Problem 8.1
(8.3.6)式を導け。
(式の内容は参照文献をご確認ください)
$$
\begin{align*}
U(x,y,\lambda)&=f(\lambda)U_{\mathcal{A}}(x,y)+g(\lambda)U_{\mathcal{B}}(x,y)\\
&=f(\lambda)\left(\frac{m_x}{2}\omega_x^2x^2+\frac{m_y}{2}\omega_y^2y^2\right)+g(\lambda)\left(\frac{m_x}{2}\omega_x^2x^2+\frac{m_y}{2}\omega_y^2y^2+\kappa xy\right)\\
&=\frac{\{f(\lambda)+g(\lambda)\}m_x\omega_x^2}{2}\left[x+\frac{g(\lambda)\kappa y}{\{f(\lambda)+g(\lambda)\}m_x\omega_x^2}\right]^2+\left[\frac{m_x\omega_x^2m_y\omega_y^2\{f(\lambda)+g(\lambda)\}^2-\kappa^2g^2(\lambda)}{2\{f(\lambda)+g(\lambda)\}m_x\omega_x^2}\right]y^2
\end{align*}
$$
より,
$$
\begin{align*}
P(\lambda)&=\langle\delta(\lambda'-\lambda)\rangle_{\lambda'}\\
&\propto \int_{-\infty}^{\infty}{\rm d}x\int_{-\infty}^{\infty}{\rm d}y\exp\left[-\beta\left\{f(\lambda)\left(\frac{m_x}{2}\omega_x^2x^2+\frac{m_y}{2}\omega_y^2y^2\right)+g(\lambda)\left(\frac{m_x}{2}\omega_x^2x^2+\frac{m_y}{2}\omega_y^2y^2+\kappa xy\right)\right\}\right]\\
&\propto \int_{-\infty}^{\infty}{\rm d}y\exp\left(-\beta\left[\frac{m_x\omega_x^2m_y\omega_y^2\{f(\lambda)+g(\lambda)\}^2-\kappa^2g^2(\lambda)}{2\{f(\lambda)+g(\lambda)\}m_x\omega_x^2}\right]y^2\right) \int_{-\infty}^{\infty}{\rm d}x\exp\left(-\beta\frac{\{f(\lambda)+g(\lambda)\}m_x\omega_x^2}{2}\left[x+\frac{g(\lambda)\kappa y}{\{f(\lambda)+g(\lambda)\}m_x\omega_x^2}\right]^2\right)\\
&\propto\sqrt{\frac{2\pi}{\beta\{f(\lambda)+g(\lambda)\}m_x\omega_x^2}}\int_{-\infty}^{\infty}{\rm d}y\exp\left(-\beta\left[\frac{m_x\omega_x^2m_y\omega_y^2\{f(\lambda)+g(\lambda)\}^2-\kappa^2g^2(\lambda)}{2\{f(\lambda)+g(\lambda)\}m_x\omega_x^2}\right]y^2\right)\\
&\propto\frac{2\pi}{\beta}\frac{1}{\sqrt{m_x\omega_x^2m_y\omega_y^2\{f(\lambda)+g(\lambda)\}^2-\kappa^2g^2(\lambda)}}
\end{align*}
$$
$${2\pi/\beta}$$は分母と分子でキャンセルされることを考慮すると,
$$
\begin{align*}
\therefore P(\lambda)&=\frac{C}{\sqrt{m_x\omega_x^2m_y\omega_y^2\{f(\lambda)+g(\lambda)\}^2-\kappa^2g^2(\lambda)}}
\end{align*}
$$
Problem 8.2
熱力学積分法を用いて(8.3.6)式の自由エネルギー形状を計算するプログラムを書け。積分値が正しい自由エネルギー差$${A(1)-A(0)}$$と高精度に一致するために必要となる$${\lambda}$$点の数はどの程度になるであろうか?
pythonによる実装例を以下に示す。$${m_x=m_y=1, \omega_x=1, \omega_y=2,k_{\rm B}T=1,\kappa=1}$$とし,また$${f(\lambda)=(\lambda^2-1)^2, g(\lambda)=((\lambda-1)^2-1)^2}$$と選んだ。温度制御には$${M=2}$$のNose-Hoover-chainを用いた。
# Import modules
from scipy import integrate
import itertools
import numpy as np
import sys
num_win = int(sys.argv[1])
random_seed = int(sys.argv[2])
np.random.seed(seed = random_seed)
# Input parameters
N_c = 4 # The number of decompotiosion for the operator exp(i * L_NHC * dt / 2)
weight = np.array([1, 1]) # Atomic weights
M = 2 # The number of chains
Q = 1 # The time scale parameter for all chains
omega = np.array([1, 2]) # Angular velocities
kappa = 1.0 # Coupling constant
kbT = 1 # Target temperature
dt = 0.01 # Time step
n_step = 999999999 # The number of replica exchange trials
# Define Lambda windows
Lambda = np.linspace(0.0, 1.0, num_win)
# Initial coordinates in extended phase space
x = np.array([0, 0] + list(np.random.normal(0, np.sqrt(weight * kbT))) + [0,] * M + [np.random.normal(0, 1),] * M)
x = np.array([x,] * (num_win - 2))
# Seven weights of the Yoshida scheme for a sixth-order scheme
N_sy = 7
w = [0] * N_sy
w[0] = w[6] = 0.784513610477560
w[1] = w[5] = 0.235573213359357
w[2] = w[4] = -1.17767998417887
w[3] = 1 - 2 * np.sum(w[:3])
# Define functions
def integrateNHC(x):
for n_c, n_sy in itertools.product(range(N_c), range(N_sy)):
scale = 1.0
KE = np.sum(x[:,2:4] ** 2 / weight, axis = 1)
delta_j = w[n_sy] * dt / N_c
x[:,-1] += 0.25 * delta_j * (x[:,-2] ** 2 / Q - kbT)
for m in range(2 + 2 * M, 4 + M, -1):
x[:,m] *= np.exp(-0.125 * delta_j * x[:,m + 1])
x[:,m] += 0.25 * delta_j * (x[:,m - 1] ** 2 / Q - kbT)
x[:,m] *= np.exp(-0.125 * delta_j * x[:,m + 1])
x[:,4 + M] *= np.exp(-0.125 * delta_j * x[:,5 + M])
x[:,4 + M] += 0.25 * delta_j * (KE - 2 * kbT)
x[:,4 + M] *= np.exp(-0.125 * delta_j * x[:,5 + M])
scale *= np.exp(-0.5 * delta_j * x[:,4 + M] / Q)
KE *= np.exp(-1.0 * delta_j * x[:,4 + M] / Q)
for m in range(4, 4 + M):
x[:,m] += 0.5 * delta_j * x[:,m + M]
x[:,4 + M] *= np.exp(-0.125 * delta_j * x[:,5 + M])
x[:,4 + M] += 0.25 * delta_j * (KE - 2 * kbT)
x[:,4 + M] *= np.exp(-0.125 * delta_j * x[:,5 + M])
for m in range(5 + M, 3 + 2 * M, 1):
x[:,m] *= np.exp(-0.125 * delta_j * x[:,m + 1])
x[:,m] += 0.25 * delta_j * (x[:,m - 1] ** 2 / Q - kbT)
x[:,m] *= np.exp(-0.125 * delta_j * x[:,m + 1])
x[:,-1] += 0.25 * delta_j * (x[:,-2] ** 2 / Q - kbT)
x[:, 2:4] *= scale.reshape((num_win - 2 , 1))
return x
def f(L):
return (L ** 2 - 1) ** 2
def g(L):
return ((L - 1) ** 2 - 1) ** 2
def U(x, L):
U0 = 0.5 * np.sum(weight * (omega * x[0:2]) ** 2)
U1 = kappa * x[0] * x[1]
return f(L) * U0 + g(L) * (U0 + U1)
def F(x, L):
F0 = -weight * omega ** 2 * x.T[0:2].T
F1 = -kappa * x.T[0:2][::-1].T
return f(L).reshape((num_win - 2, 1)) * F0 + g(L).reshape((num_win - 2, 1)) * (F0 + F1)
def dUdL(x, L):
U0 = 0.5 * np.sum(weight * (omega * x.T[0:2].T) ** 2, axis = 1)
U1 = kappa * x.T[0] * x.T[1]
return 4 * L * (L ** 2 - 1) * U0 + 4 * (L - 1) * ((L - 1) ** 2 - 1) * (U0 + U1)
def exchangeReplicas(x, Lambda, start_index = 0):
for i in range(start_index, len(x) - 1, 2):
U0 = U(x[i], Lambda[i])
U1 = U(x[i], Lambda[i + 1])
U2 = U(x[i + 1], Lambda[i])
U3 = U(x[i + 1], Lambda[i + 1])
Delta = (U0 + U3 - U1 - U2) / kbT
A = np.min([1, np.exp(Delta)])
if A >= np.random.rand():
x0_new = x[i + 1]
x1_new = x[i]
x[i] = x0_new
x[i + 1] = x1_new
return x
#-------- The below is the code --------#
# Analytical result
A_ana = 0.5 * kbT * np.log(weight[0] * weight[1] * (omega[0] * omega[1] * (f(Lambda) + g(Lambda))) ** 2 - (kappa * g(Lambda)) ** 2)
A_ana -= np.min(A_ana)
integrand = [0, ]
samples = []
interval = 100
# Equilibrate before sampling
for _ in range(1000):
x = integrateNHC(x)
x[:,2:4] += 0.5 * dt * F(x, Lambda[1:-1])
x[:,0:2] += dt * x[:,2:4] / weight
x[:,2:4] += 0.5 * dt * F(x, Lambda[1:-1])
x = integrateNHC(x)
for i in range(n_step):
# Update phase space coordinates
for _ in range(interval):
x = integrateNHC(x)
x[:,2:4] += 0.5 * dt * F(x, Lambda[1:-1])
x[:,0:2] += dt * x[:,2:4] / weight
x[:,2:4] += 0.5 * dt * F(x, Lambda[1:-1])
x = integrateNHC(x)
samples.append(dUdL(x, Lambda[1:-1]))
dudl_mean = np.mean(samples, axis = 0)
dudl_ste = np.std(samples, axis = 0) / np.sqrt(len(samples))
dudl_err = abs(dudl_ste / dudl_mean)
dudl_err_min = np.min(dudl_err)
dudl_err_max = np.max(dudl_err)
sys.stdout.write(f"\r {i:0>6}: {dudl_err_min:.5f} - {dudl_err_max:.5f}")
sys.stdout.flush()
if (i > 100) and (dudl_err_max < 1e-2):
break
start_index = 1 if i % 2 == 0 else 0
x = exchangeReplicas(x, Lambda[1:-1], start_index = start_index)
print("\n")
integrand = np.mean(np.array(samples), axis = 0)
integrand = np.append(0, integrand)
integrand = np.append(integrand, 0)
A_num = np.array([0] + [integrate.simps(integrand[:i], Lambda[:i]) for i in range(2, len(integrand) + 1)])
A_num -= np.min(A_num)
for L, a_num, a_ana, I in zip(Lambda, A_num, A_ana, integrand):
print(L, a_num, a_ana, I)
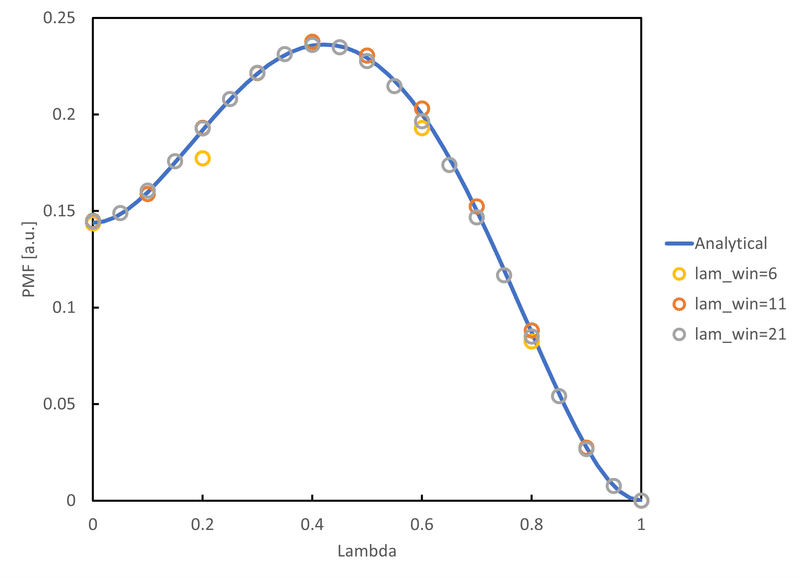
$${\lambda=0,1}$$の自由エネルギー差は$${\lambda}$$ window数が6でも解析解に高精度に一致する結果が得られた。
Problem 8.3
自由エネルギー摂動法を用いて(8.3.6)式から自由エネルギー差$${A(1)-A(0)}$$を計算するプログラムを書け。ワンステップの摂動で正しい解が得られるであろうか,それとも中間状態が必要になるであろうか?
pythonによる実装例を以下に示す。$${m_x=m_y=1, \omega_x=1, \omega_y=2,k_{\rm B}T=1,\kappa=1}$$とし,また$${f(\lambda)=1-\lambda, g(\lambda)=\lambda}$$と選んだ。温度制御には$${M=2}$$のNose-Hoover-chainを用いた。
# Import modules
from scipy import integrate
import itertools
import numpy as np
import sys
num_win = int(sys.argv[1])
random_seed = int(sys.argv[2])
np.random.seed(seed = random_seed)
# Input parameters
N_c = 4 # The number of decompotiosion for the operator exp(i * L_NHC * dt / 2)
weight = np.array([1, 1]) # Atomic weights
M = 2 # The number of chains
Q = 1 # The time scale parameter for all chains
omega = np.array([1, 2]) # Angular velocities
kappa = 1.0 # Coupling constant
kbT = 1 # Target temperature
dt = 0.01 # Time step
n_step = 999999999 # The number of replica exchange trials
# Define Lambda windows
Lambda = np.linspace(0.0, 1.0, num_win)
# Initial coordinates in extended phase space
x = np.array([0, 0] + list(np.random.normal(0, np.sqrt(weight * kbT))) + [0,] * M + [np.random.normal(0, 1),] * M)
x = np.array([x,] * (num_win - 1))
# Seven weights of the Yoshida scheme for a sixth-order scheme
N_sy = 7
w = [0] * N_sy
w[0] = w[6] = 0.784513610477560
w[1] = w[5] = 0.235573213359357
w[2] = w[4] = -1.17767998417887
w[3] = 1 - 2 * np.sum(w[:3])
# Define functions
def integrateNHC(x):
for n_c, n_sy in itertools.product(range(N_c), range(N_sy)):
scale = 1.0
KE = np.sum(x[:,2:4] ** 2 / weight, axis = 1)
delta_j = w[n_sy] * dt / N_c
x[:,-1] += 0.25 * delta_j * (x[:,-2] ** 2 / Q - kbT)
for m in range(2 + 2 * M, 4 + M, -1):
x[:,m] *= np.exp(-0.125 * delta_j * x[:,m + 1])
x[:,m] += 0.25 * delta_j * (x[:,m - 1] ** 2 / Q - kbT)
x[:,m] *= np.exp(-0.125 * delta_j * x[:,m + 1])
x[:,4 + M] *= np.exp(-0.125 * delta_j * x[:,5 + M])
x[:,4 + M] += 0.25 * delta_j * (KE - 2 * kbT)
x[:,4 + M] *= np.exp(-0.125 * delta_j * x[:,5 + M])
scale *= np.exp(-0.5 * delta_j * x[:,4 + M] / Q)
KE *= np.exp(-1.0 * delta_j * x[:,4 + M] / Q)
for m in range(4, 4 + M):
x[:,m] += 0.5 * delta_j * x[:,m + M]
x[:,4 + M] *= np.exp(-0.125 * delta_j * x[:,5 + M])
x[:,4 + M] += 0.25 * delta_j * (KE - 2 * kbT)
x[:,4 + M] *= np.exp(-0.125 * delta_j * x[:,5 + M])
for m in range(5 + M, 3 + 2 * M, 1):
x[:,m] *= np.exp(-0.125 * delta_j * x[:,m + 1])
x[:,m] += 0.25 * delta_j * (x[:,m - 1] ** 2 / Q - kbT)
x[:,m] *= np.exp(-0.125 * delta_j * x[:,m + 1])
x[:,-1] += 0.25 * delta_j * (x[:,-2] ** 2 / Q - kbT)
x[:, 2:4] *= scale.reshape((num_win - 1, 1))
return x
def f(L):
return (1 - L) #(L ** 2 - 1) ** 2
def g(L):
return L # ((L - 1) ** 2 - 1) ** 2
def U(x, L):
U0 = 0.5 * np.sum(weight * (omega * x[0:2]) ** 2)
U1 = kappa * x[0] * x[1]
return f(L) * U0 + g(L) * (U0 + U1)
def F(x, L):
F0 = -weight * omega ** 2 * x.T[0:2].T
F1 = -kappa * x.T[0:2][::-1].T
return f(L).reshape((num_win - 1, 1)) * F0 + g(L).reshape((num_win - 1, 1)) * (F0 + F1)
#-------- The below is the code --------#
# Analytical result
A_ana = 0.5 * kbT * np.log(weight[0] * weight[1] * (omega[0] * omega[1] * (f(Lambda) + g(Lambda))) ** 2 - (kappa * g(Lambda)) ** 2)
dA_ana = A_ana[-1] - A_ana[0]
integrand = [0, ]
samples = []
interval = 100
# Equilibrate before sampling
for _ in range(1000):
x = integrateNHC(x)
x[:,2:4] += 0.5 * dt * F(x, Lambda[:-1])
x[:,0:2] += dt * x[:,2:4] / weight
x[:,2:4] += 0.5 * dt * F(x, Lambda[:-1])
x = integrateNHC(x)
dA_err = 1
for i in range(n_step):
# Update phase space coordinates
for _ in range(interval):
x = integrateNHC(x)
x[:,2:4] += 0.5 * dt * F(x, Lambda[:-1])
x[:,0:2] += dt * x[:,2:4] / weight
x[:,2:4] += 0.5 * dt * F(x, Lambda[:-1])
x = integrateNHC(x)
exp_dU = np.exp([-1 * (U(x[j], Lambda[j + 1]) - U(x[j], Lambda[j])) / kbT for j in range(num_win - 1)])
samples.append(exp_dU)
dA_num = -1 * kbT * np.sum(np.log(np.mean(samples, axis = 0)))
dA_err = abs((dA_ana - dA_num) / dA_ana)
sys.stdout.write(f"\r {i:0>6}: {dA_num:.3f},{dA_err:.5f}")
sys.stdout.flush()
if dA_err < 1e-4:
break
今回作成したプログラムにおいては,中間状態を設けなくても解析解に収束する数値解が得られた。
Problem 8.4
(8.7.25)式を導け。
(式の内容は参照文献をご確認ください)
$$
\begin{align*}
\mathbf{a}&=\begin{bmatrix}a_1&\cdots&a_{3N}\end{bmatrix}^{\rm T}\\
&:=\begin{bmatrix}\frac{1}{\sqrt{m_1}}\left(\frac{\partial \sigma}{\partial\mathbf{r}_1}\right)^{\rm T}&\cdots&\frac{1}{\sqrt{m_N}}\left(\frac{\partial \sigma}{\partial\mathbf{r}_N}\right)^{\rm T}\end{bmatrix}^{\rm T}\\
\mathbf{p}&=\begin{bmatrix}p_1&\cdots&p_{3N}\end{bmatrix}^{\rm T}\\
&:=\begin{bmatrix}\frac{\mathbf{p}_1^{\rm T}}{\sqrt{m_1}}&\cdots&\frac{\mathbf{p}_N^{\rm T}}{\sqrt{m_N}}\end{bmatrix}^{\rm T}\\
\end{align*}
$$
と定義しておく。
この表記を用いて,(8.7.24)式を$${p_1}$$に関して積分すると,
$$
\begin{align*}
\mathcal{Z}&=\int{\rm d}^N\mathbf{r}{\rm d}^{3N}pz(\mathbf{r}){\rm e}^{-\beta\mathcal{H}(\mathbf{r},\mathbf{p})}\delta(\sigma(\mathbf{r}))\delta(\mathbf{a}^{\rm T}\mathbf{p})\\
&=\prod_{i=1}^Nm_i^{3/2}\int{\rm d}^N\mathbf{r}z(\mathbf{r}){\rm e}^{-\beta U(\mathbf{r})}\delta(\sigma(\mathbf{r}))\int{\rm d}^{3N-1}p\int_{-\infty}^{\infty}{\rm d}p_1{\rm e}^{-\frac{\beta}{2}\sum_{i=1}^{3N}p_i^2}\frac{1}{a_1}\delta\left(p_1-\sum_{j=2}^{3N}a_jp_j / a_1\right)\\
&=\prod_{i=1}^Nm_i^{3/2}\int{\rm d}^N\mathbf{r}z(\mathbf{r}){\rm e}^{-\beta U(\mathbf{r})}\delta(\sigma(\mathbf{r}))\frac{1}{a_1}\int{\rm d}^{3N-1}p\exp\left[-\frac{\beta}{2}\left\{\frac{1}{a_1^2}\left(\sum_{j=2}^{3N}a_jp_j \right)^2+\sum_{i=2}^{3N}p_i^2\right\}\right]\\
\end{align*}
$$
次に$${p_2}$$に積分すると,
$$
\begin{align*}
\frac{1}{a_1}\int{\rm d}^{3N-1}p\exp\left[-\frac{\beta}{2}\left\{\left(\sum_{j=2}^{3N}a_jp_j / a_1\right)^2+\sum_{i=2}^{3N}p_i^2\right\}\right]&=\frac{1}{a_1}\int{\rm d}^{3N-1}p\exp\left[-\frac{\beta}{2}\left\{\left(\frac{a_1^2+a_2^2}{a_1^2}\right)\left(p_2+\frac{a_2}{a_1^2+a_2^2}\sum_{j=3}^{3N}a_jp_j \right)^2+\left(\frac{1}{a_1^2+a_2^2}\right)\left(\sum_{j=3}^{3N}a_jp_j \right)^2+\sum_{i=3}^{3N}p_i^2\right\}\right]\\
&=\sqrt{\frac{2\pi}{\beta}}\frac{1}{\sqrt{a_1^2+a_2^2}}\int{\rm d}^{3N-2}p\exp\left[-\frac{\beta}{2}\left\{\left(\frac{1}{a_1^2+a_2^2}\right)\left(\sum_{j=3}^{3N}a_jp_j \right)^2+\sum_{i=3}^{3N}p_i^2\right\}\right]\\
\end{align*}
$$
となる。$${p_3}$$以降についても順に積分していくと,
$$
\begin{align*}
{\rm r.h.s}&=\left(\frac{2\pi}{\beta}\right)^{2/2}\frac{1}{\sqrt{a_1^2+a_2^2+a_3^2}}\int{\rm d}^{3N-3}p\exp\left[-\frac{\beta}{2}\left\{\left(\frac{1}{a_1^2+a_2^2+a_3^3}\right)\left(\sum_{j=4}^{3N}a_jp_j \right)^2+\sum_{i=4}^{3N}p_i^2\right\}\right]\\
&\vdots\\
&=\left(\frac{2\pi}{\beta}\right)^{(3N-1)/2}\frac{1}{\sqrt{\sum_{i=1}^{3N}a_i^2}}\\
&=\left(\frac{2\pi}{\beta}\right)^{(3N-1)/2}\frac{1}{\sqrt{z(\mathbf{r})}}\\
\end{align*}
$$
となる。
以上より,
$$
\begin{align*}
\mathcal{Z}&\propto\int{\rm d}^N\mathbf{r}z^{1/2}(\mathbf{r}){\rm e}^{-\beta U(\mathbf{r})}\delta(\sigma(\mathbf{r}))
\end{align*}
$$
が得られる。
Problem 8.5
(8.10.22)式を導け。
(式の内容は参照文献をご確認ください)
$$
\begin{align*}
P(x)&\propto\int_{-\infty}^{\infty}{\rm d}y\exp\left[-\beta\left\{D_0(x^2-a^2)^2+\frac{k}{2}y^2+\lambda xy\right\}\right]\\
&\propto\exp\left[-\beta\left\{D_0(x^2-a^2)^2-\frac{\lambda^2x^2}{2k}\right\}\right]\int_{-\infty}^{\infty}{\rm d}y\exp\left[-\frac{\beta k}{2}\left(y+\lambda x / k\right)^2\right]\\
&\propto\exp\left[-\beta\left\{D_0(x^2-a^2)^2-\frac{\lambda^2x^2}{2k}\right\}\right]\\
\therefore A(x)&=-\frac{1}{\beta}\ln P(x)\\
&=D_0(x^2-a^2)^2-\frac{\lambda^2x^2}{2k}
\end{align*}
$$
Problem 8.6
以下のポテンシャルで表される2自由度$${x,y}$$の古典系を考える。
$$
\begin{align*}
U(x,y)&=\frac{U_0}{a^4}\left(x^2-a^2\right)^2+\frac{1}{2}ky^2+\lambda xy
\end{align*}
$$
$${x}$$を$${x=-a}$$から$${x=0}$$に移動させる過程を考える。
a. カノニカルアンサンブルにおいて,この過程のヘルムホルツ自由エネルギー差$${\Delta A}$$を計算せよ。
b. $${x}$$が$${x=-a}$$から$${x=0}$$に瞬間的に移動する不可逆過程を考える。この過程において,$${y}$$は位置を変えずに固定される。この過程における系に及ぼされる仕事はポテンシャルエネルギーの変化で表される。
$$
\begin{align*}
W&=U(0,y)-U(-a,y)
\end{align*}
$$
初期条件$${x=-a}$$をカノニカルアンサンブルから用意したとして$${W}$$のアンサンブル平均を計算し,$${\langle W\rangle>\Delta A}$$を示せ。
c. b.と同様にして今度は$${\exp(-\beta W)}$$のアンサンブル平均を計算し,Jarzynski等式$${\langle \exp(-\beta W)\rangle=\exp(-\beta A)}$$が成立することを示せ。
a.
$$
\begin{align*}
\Delta A&= A(0) - A(-a)\\
&=U_0+\frac{\lambda^2a^2}{2k}
\end{align*}
$$
b.
$$
\begin{align*}
W(y)&= U(0,y)-U(-a,y)\\
&=U_0+\lambda a y\\
&=\left(U_0+\frac{\lambda^2a^2}{k}\right)+\lambda a\left(y-\frac{\lambda a}{k}\right)\\
P(y|x=-a)&=\sqrt{\frac{\beta k}{2\pi}}\exp\left[-\frac{\beta k}{2}\left(y-\frac{\lambda a}{k}\right)^2\right]
\end{align*}
$$
より,
$$
\begin{align*}
\langle W\rangle&=\int_{-\infty}^{\infty}{\rm d}yW(y)P(y|x=-a)\\
&=U_0+\frac{\lambda^2a^2}{k}\\
&>\Delta A
\end{align*}
$$
c.
$$
\begin{align*}
\langle \exp(-\beta W)\rangle&=\int_{-\infty}^{\infty}{\rm d}y\exp(-\beta W(y))P(y|x=-a)\\
&=\sqrt{\frac{\beta k}{2\pi}}\exp\left[-\beta\left(U_0+\frac{\lambda^2a^2}{k}\right)\right]\int_{-\infty}^{\infty}{\rm d}y\exp\left[-\beta\lambda a\left(y-\frac{\lambda a}{k}\right) -\frac{\beta k}{2}\left(y-\frac{\lambda a}{k}\right)^2\right]\\
&=\sqrt{\frac{\beta k}{2\pi}}\exp\left[-\beta\left(U_0+\frac{\lambda^2a^2}{2k}\right)\right]\int_{-\infty}^{\infty}{\rm d}y\exp\left[-\frac{\beta k\lambda}{2}y^2\right]\\
&=\exp\left[-\beta\left(U_0+\frac{\lambda^2a^2}{2k}\right)\right]=\exp\left[-\beta\Delta A\right]
\end{align*}
$$
Problem 8.7
以下の拘束条件に対するblue moonアンサンブルのunbiasing因子$${z(\mathbf{r})}$$と曲率因子$${G(\mathbf{r})}$$((8.7.20)式,(8.7.31)式を見よ)を計算せよ。
a. 2つの位置$${\mathbf{r}_1,\mathbf{r}_2}$$の間の距離
b. $${\mathbf{r}_1,\mathbf{r}_2}$$の距離と$${\mathbf{r}_1,\mathbf{r}_3}$$の距離の差分($${|\mathbf{r}_1-\mathbf{r}_2|-|\mathbf{r}_1-\mathbf{r}_3|}$$)
c. $${\mathbf{r}_2-\mathbf{r}_1,\mathbf{r}_3-\mathbf{r}_1}$$のなす角
d. $${\mathbf{r}_1,\mathbf{r}_2,\mathbf{r}_3,\mathbf{r}_4}$$からなる二面角
a. $${\sigma(\mathbf{r})=|\mathbf{r}_1-\mathbf{r}_2|-d_{12}=0}$$のとき,
$$
\begin{align*}
\frac{\partial \sigma(\mathbf{r})}{\partial\mathbf{r}_1}&=\frac{\mathbf{r}_1-\mathbf{r}_2}{|\mathbf{r}_1-\mathbf{r}_2|}=:\frac{\mathbf{r}_1-\mathbf{r}_2}{r_{12}}\\
\frac{\partial \sigma(\mathbf{r})}{\partial\mathbf{r}_2}&=-\frac{\mathbf{r}_1-\mathbf{r}_2}{r_{12}}\\
\frac{\partial^2 \sigma(\mathbf{r})}{\partial\mathbf{r}_1\partial\mathbf{r}_2}&=\frac{(\mathbf{r}_1-\mathbf{r}_2)(\mathbf{r}_1-\mathbf{r}_2)^{\rm T}}{r_{12}^3}-\frac{\mathbf{I}}{r_{12}}\\
\frac{\partial^2 \sigma(\mathbf{r})}{\partial\mathbf{r}_1^2}&=\frac{\partial^2 \sigma(\mathbf{r})}{\partial\mathbf{r}_2^2}\\
&=-\frac{(\mathbf{r}_1-\mathbf{r}_2)(\mathbf{r}_1-\mathbf{r}_2)^{\rm T}}{r_{12}^3}+\frac{\mathbf{I}}{r_{12}}\\
\end{align*}
$$
より,
$$
\begin{align*}
z(\mathbf{r})&=\frac{1}{m_1}+\frac{1}{m_2}\\
G(\mathbf{r})&=0
\end{align*}
$$
a. $${\sigma(\mathbf{r})=(|\mathbf{r}_1-\mathbf{r}_2|-|\mathbf{r}_1-\mathbf{r}_3|)-d_{12-13}=0}$$のとき,
$$
\begin{align*}
\frac{\partial \sigma(\mathbf{r})}{\partial\mathbf{r}_1}&=\frac{\mathbf{r}_1-\mathbf{r}_2}{|\mathbf{r}_1-\mathbf{r}_2|}-\frac{\mathbf{r}_1-\mathbf{r}_3}{|\mathbf{r}_1-\mathbf{r}_3|}=:\mathbf{e}_{12}-\mathbf{e}_{13}\\
\frac{\partial \sigma(\mathbf{r})}{\partial\mathbf{r}_2}&=-\mathbf{e}_{12}\\
\frac{\partial \sigma(\mathbf{r})}{\partial\mathbf{r}_3}&=\mathbf{e}_{13}\\
\frac{\partial^2 \sigma(\mathbf{r})}{\partial\mathbf{r}_1^2}&=-\frac{\mathbf{e}_{12}\mathbf{e}_{12}^{\rm T}-\mathbf{I}}{|\mathbf{r}_1-\mathbf{r}_2|}+\frac{\mathbf{e}_{13}\mathbf{e}_{13}^{\rm T}-\mathbf{I}}{|\mathbf{r}_1-\mathbf{r}_3|}\\
&=:-\frac{\mathbf{e}_{12}\mathbf{e}_{12}^{\rm T}-\mathbf{I}}{r_{12}}+\frac{\mathbf{e}_{13}\mathbf{e}_{13}^{\rm T}-\mathbf{I}}{r_{13}}\\
\frac{\partial^2 \sigma(\mathbf{r})}{\partial\mathbf{r}_1\partial\mathbf{r}_2}&=\frac{\mathbf{e}_{12}\mathbf{e}_{12}^{\rm T}-\mathbf{I}}{r_{12}}\\
\frac{\partial^2 \sigma(\mathbf{r})}{\partial\mathbf{r}_1\partial\mathbf{r}_3}&=-\frac{\mathbf{e}_{13}\mathbf{e}_{13}^{\rm T}-\mathbf{I}}{r_{13}}\\
\frac{\partial^2 \sigma(\mathbf{r})}{\partial\mathbf{r}_2^2}
&=-\frac{\mathbf{e}_{12}\mathbf{e}_{12}^{\rm T}-\mathbf{I}}{r_{12}}\\
\frac{\partial^2 \sigma(\mathbf{r})}{\partial\mathbf{r}_3^2}
&=\frac{\mathbf{e}_{13}\mathbf{e}_{13}^{\rm T}-\mathbf{I}}{r_{13}}\\
\end{align*}
$$
より,
$$
\begin{align*}
z(\mathbf{r})&=\frac{2}{m_1}(1-\cos\theta)+\frac{1}{m_2}+\frac{1}{m_3}\\
G(\mathbf{r})&=\frac{1}{m_1^2z^2(\mathbf{r})}\left(\frac{1}{r_{13}}-\frac{1}{r_{12}}\right)\left\{(1-\cos\theta)^2-\|\mathbf{e}_{12}-\mathbf{e}_{13}\|^2\right\}
\end{align*}
$$
ここで,$${\theta}$$は$${\mathbf{r}_3-\mathbf{r}_1}$$と$${\mathbf{r}_2-\mathbf{r}_1}$$のなす角である。
c. $${\sigma(\mathbf{r})=\mathbf{e}_{12}^{\rm T}\mathbf{e}_{13}-\cos\theta_0=0}$$のとき,
$$
\begin{align*}
\frac{\partial \sigma(\mathbf{r})}{\partial\mathbf{r}_1}&=\frac{1}{r_{13}}\left(\mathbf{e}_{12}-\cos\theta_0\mathbf{e}_{13}\right)+\frac{1}{r_{12}}\left(\mathbf{e}_{13}-\cos\theta_0\mathbf{e}_{12}\right)\\
\frac{\partial \sigma(\mathbf{r})}{\partial\mathbf{r}_2}&=-\frac{1}{r_{12}}\left(\mathbf{e}_{13}-\cos\theta_0\mathbf{e}_{12}\right)\\
\frac{\partial \sigma(\mathbf{r})}{\partial\mathbf{r}_3}&=-\frac{1}{r_{13}}\left(\mathbf{e}_{12}-\cos\theta_0\mathbf{e}_{13}\right)\\
\end{align*}
$$
より,
$$
\begin{align*}
z(\mathbf{r})&=\left\{\left(\frac{1}{m_1}+\frac{1}{m_2}\right)\frac{1}{r_{12}^2}+\left(\frac{1}{m_1}+\frac{1}{m_3}\right)\frac{1}{r_{13}^2}-\frac{2\cos\theta_0}{m_1r_{12}r_{13}}\right\}\sin^2\theta_0\\
\end{align*}
$$
$${G(\mathbf{r})}$$については計算がしんどいので省略。。。
d. $${\sigma(\mathbf{r})=(\mathbf{e}_{12}\times\mathbf{e}_{23})^{\rm T}(\mathbf{e}_{23}\times\mathbf{e}_{34})-\cos\theta_0=0}$$として微分を求めればよい。具体的な計算はしんどいので省略。。。
Problem 8.8
図8.1で示されているエンザイムと阻害剤の結合自由エネルギー計算に対して,間接過程にそって計算を実行するために必要となるアルゴリズムの詳細を示せ。各終点を表すためにどのようなポテンシャルエネルギー関数が必要となるであろうか?

ポテンシャルエネルギー関数を以下のように定義する
$$
\begin{align*}
U_{\rm E}&: エンザイムの内部ポテンシャル\\
U_{\rm I}&: 阻害剤の内部ポテンシャル\\
U_{\rm S}&: 阻害剤の内部ポテンシャル\\
U_{\rm E-I}&: エンザイムと阻害剤の相互作用エネルギー\\
U_{\rm E-S}&: エンザイムと溶媒の相互作用エネルギー\\
U_{\rm l-S}&: エンザイムと溶媒の相互作用エネルギー\\
\end{align*}
$$
$${\Delta A_1}$$はエンザイムと阻害剤の脱溶媒和自由エネルギーの和であり
,それぞれポテンシャルエネルギーを$${U_{\rm E}+U_{\rm S}+U_{\rm E-S}\rightarrow U_{\rm E}+U_{\rm S}}$$,$${U_{\rm I}+U_{\rm S}+U_{\rm I-S}\rightarrow U_{\rm I}+U_{\rm S}}$$と変化させた際の自由エネルギー差として計算される。
$${\Delta A_2}$$はエンザイムと阻害剤の真空下での結合自由エネルギーであり
,原理的にはポテンシャルエネルギーを$${U_{\rm E}+U_{\rm I}\rightarrow U_{\rm E}+U_{\rm I}+U_{\rm E-I}}$$と変化させた際の自由エネルギー差として計算される。ただし,現実的には結合サイト周辺でのサンプリングにバイアスをかけないと計算を収束させることが難しい。そのため,阻害剤をエンザイムの結合サイト周辺に閉じ込めるようなポテンシャル$${U_{\rm const}}$$を新たに導入し,$${U_{\rm E}+U_{\rm I}\rightarrow U_{\rm E}+U_{\rm I}+U_{\rm const}\rightarrow U_{\rm E}+U_{\rm I}+U_{\rm const}+U_{\rm E-I}\rightarrow U_{\rm E}+U_{\rm I}+U_{\rm E-I}}$$に対する自由エネルギー差を計算する。
$${\Delta A_3}$$はエンザイム-阻害剤複合体の溶媒和自由エネルギーの和であり
,ポテンシャルエネルギーを$${U_{\rm E}+U_{\rm I}+U_{\rm E-I}\rightarrow U_{\rm E}+U_{\rm I}+U_{\rm E-I}+U_{\rm E-S}+U_{\rm I-S}}$$と変化させた際の自由エネルギー差として計算される。
Problem 8.9
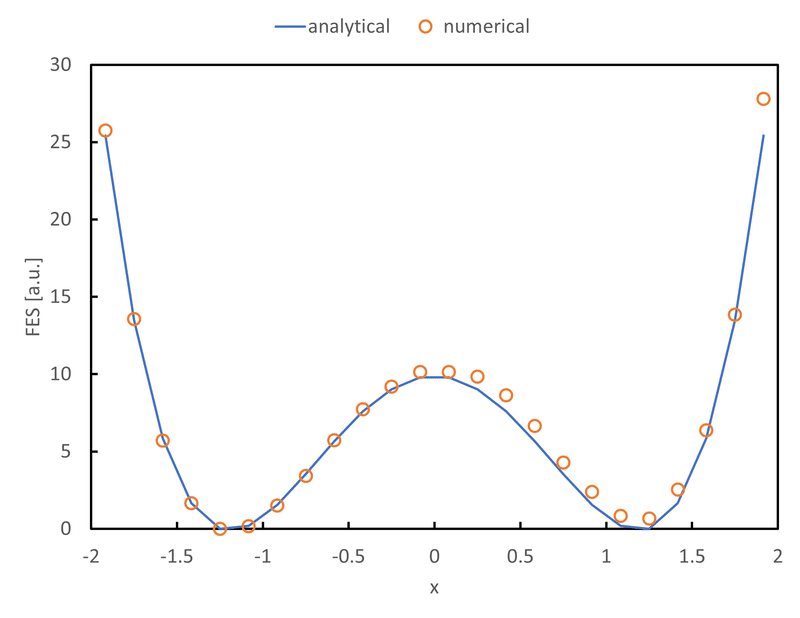
a. 問題8.6で取り扱ったポテンシャルに対応する自由エネルギープロファイル$${A(x)}$$の断熱的自由エネルギー動力学計算を実行するためのプログラムを書け。プログラムでは以下のパラメータ値を採用せよ:$${a=1, U_0=5, k_{\rm B}T_y=1, k_{\rm B}T_x=5, m_y=1, m_x=1000, \lambda=2.878}$$。$${x,y}$$の温度を制御するために個別にNose-Hoover chainsを適用せよ。
b. プログラムを利用して8.12節のヒストグラムテストを実行せよ。ヒストグラムのピークが$${p=1/2}$$に位置するであろうか?
a. pythonによる実装例を以下に示す。
# Import modules
from scipy import integrate
import itertools
import numpy as np
import sys
np.random.seed(seed = 2021)
# Input parameters
N_c = 4 # The number of decompotiosion for the operator exp(i * L_NHC * dt / 2)
weight = np.array([1000, 1]) # Atomic weights
M = 2 # The number of chains
Q = [5, 1] # The time scale parameter for NH chains
k = 1 # The spring constant
kbT = np.array([5.0, 1.0]) # Target temperature
dt = 0.05 # Time step
n_step = 999999999 # The number of replica exchange trials
a = 1 # The scale length
U_0 = 5.0 # The height of potential
Lambda = 2.878 # The coupling parameter
# Initial coordinates in extended phase space
v_i = np.random.normal(0, np.sqrt(weight * kbT), (M + 1, 2))
X_x = np.zeros(2 * (M + 1))
X_x[1] = v_i[0][0]
X_x[-2:] = v_i[:,0][-2:]
X_y = np.zeros(2 * (M + 1))
X_y[1] = v_i[0][1]
X_y[-2:] = v_i[:,1][-2:]
# Seven weights of the Yoshida scheme for a sixth-order scheme
N_sy = 7
w = [0] * N_sy
w[0] = w[6] = 0.784513610477560
w[1] = w[5] = 0.235573213359357
w[2] = w[4] = -1.17767998417887
w[3] = 1 - 2 * np.sum(w[:3])
# Define functions
def integrateNHC(x, weigh, kbT, Q):
for n_c, n_sy in itertools.product(range(N_c), range(N_sy)):
scale = 1.0
KE = x[1] ** 2 / weigh
delta_j = w[n_sy] * dt / N_c
x[-1] += 0.25 * delta_j * (x[-2] ** 2 / Q - kbT)
for m in range(2 * M, 2 + M, -1):
x[m] *= np.exp(-0.125 * delta_j * x[m + 1] / Q)
x[m] += 0.25 * delta_j * (x[m - 1] ** 2 / Q - kbT)
x[m] *= np.exp(-0.125 * delta_j * x[m + 1] / Q)
x[2 + M] *= np.exp(-0.125 * delta_j * x[3 + M] / Q)
x[2 + M] += 0.25 * delta_j * (KE - kbT)
x[2 + M] *= np.exp(-0.125 * delta_j * x[3 + M] / Q)
scale *= np.exp(-0.5 * delta_j * x[2 + M] / Q)
KE *= np.exp(-1.0 * delta_j * x[2 + M] / Q)
for m in range(2, 2 + M):
x[m] += 0.5 * delta_j * x[m + M] / Q
x[2 + M] *= np.exp(-0.125 * delta_j * x[3 + M] / Q)
x[2 + M] += 0.25 * delta_j * (KE - kbT)
x[2 + M] *= np.exp(-0.125 * delta_j * x[3 + M] / Q)
for m in range(3 + M, 2 * M + 1, 1):
x[m] *= np.exp(-0.125 * delta_j * x[m + 1] / Q)
x[m] += 0.25 * delta_j * (x[m - 1] ** 2 / Q - kbT)
x[m] *= np.exp(-0.125 * delta_j * x[m + 1] / Q)
x[-1] += 0.25 * delta_j * (x[-2] ** 2 / Q - kbT)
x[1] *= scale
return x
def A(x):
return U_0 * (x ** 2 - a ** 2) ** 2 / (a ** 4) - 0.5 * ((Lambda * x) ** 2) / k
def U(x, y):
return U_0 * (x ** 2 - a ** 2) ** 2 / (a ** 4) + 0.5 * k * y ** 2 + Lambda * x * y
def F_x(x, y):
return -4 * U_0 * x * (x ** 2 - a ** 2) / (a ** 4) - Lambda * y
def F_y(x, y):
return -k * y - Lambda * x
#-------- The below is the code --------#
# Analytical result
grids = np.linspace(-2,2,25)
grids2 = 0.5 * (grids[:-1] + grids[1:])
A_ana = A(grids2)
A_ana -= np.min(A_ana)
samples = []
interval = 100
for i in range(n_step):
# Update phase space coordinates
for _ in range(interval):
X_x = integrateNHC(X_x, weight[0], kbT[0], Q[0])
X_y = integrateNHC(X_y, weight[1], kbT[1], Q[1])
X_x[1] += 0.5 * dt * F_x(X_x[0], X_y[0])
X_y[1] += 0.5 * dt * F_y(X_x[0], X_y[0])
X_x[0] += dt * X_x[1] / weight[0]
X_y[0] += dt * X_y[1] / weight[1]
X_x[1] += 0.5 * dt * F_x(X_x[0], X_y[0])
X_y[1] += 0.5 * dt * F_y(X_x[0], X_y[0])
X_x = integrateNHC(X_x, weight[0], kbT[0], Q[0])
X_y = integrateNHC(X_y, weight[1], kbT[1], Q[1])
samples.append(X_x[0])
prob_num = np.histogram(samples, bins = grids)[0]
A_num = -1 * kbT[0] * np.log(prob_num)
A_num -= np.min(A_num)
if i > 100 and i % 500 == 0:
print("\n")
for c1, c2, c3 in zip(grids2, A_ana, A_num):
print(c1,c2,c3)
print("\n")
dA = abs((A_ana - A_num))
sys.stdout.write(f"\r {i:0>6}: {dA.min():.5f} - {dA.max():.5f}, {X_x[0]:.5f}")
sys.stdout.flush()
b. pythonによる実装例を以下に示す。
# Import modules
from scipy import integrate
import itertools
import numpy as np
import sys
import matplotlib.pyplot as plt
# Input parameters
N_c = 4 # The number of decompotiosion for the operator exp(i * L_NHC * dt / 2)
weight = np.array([1000, 1]) # Atomic weights
M = 2 # The number of chains
Q = [5, 1] # The time scale parameter for NH chains
k = 1 # The spring constant
kbT = np.array([5.0, 1.0]) # Target temperature
dt = 0.05 # Time step
n_step = 999999999 # The number of replica exchange trials
a = 1 # The scale length
U_0 = 5.0 # The height of potential
Lambda = 2.878 # The coupling parameter
# Initial coordinates in extended phase space
v_i = np.random.normal(0, np.sqrt(weight * kbT), (M + 1, 2))
X_x = np.zeros(2 * (M + 1))
X_x[1] = v_i[0][0]
X_x[-2:] = v_i[:,0][-2:]
X_y = np.zeros(2 * (M + 1))
X_y[1] = v_i[0][1]
X_y[-2:] = v_i[:,1][-2:]
# Seven weights of the Yoshida scheme for a sixth-order scheme
N_sy = 7
w = [0] * N_sy
w[0] = w[6] = 0.784513610477560
w[1] = w[5] = 0.235573213359357
w[2] = w[4] = -1.17767998417887
w[3] = 1 - 2 * np.sum(w[:3])
# Define functions
def integrateNHC(x, weigh, kbT, Q):
for n_c, n_sy in itertools.product(range(N_c), range(N_sy)):
scale = 1.0
KE = x[1] ** 2 / weigh
delta_j = w[n_sy] * dt / N_c
x[-1] += 0.25 * delta_j * (x[-2] ** 2 / Q - kbT)
for m in range(2 * M, 2 + M, -1):
x[m] *= np.exp(-0.125 * delta_j * x[m + 1] / Q)
x[m] += 0.25 * delta_j * (x[m - 1] ** 2 / Q - kbT)
x[m] *= np.exp(-0.125 * delta_j * x[m + 1] / Q)
x[2 + M] *= np.exp(-0.125 * delta_j * x[3 + M] / Q)
x[2 + M] += 0.25 * delta_j * (KE - kbT)
x[2 + M] *= np.exp(-0.125 * delta_j * x[3 + M] / Q)
scale *= np.exp(-0.5 * delta_j * x[2 + M] / Q)
KE *= np.exp(-1.0 * delta_j * x[2 + M] / Q)
for m in range(2, 2 + M):
x[m] += 0.5 * delta_j * x[m + M] / Q
x[2 + M] *= np.exp(-0.125 * delta_j * x[3 + M] / Q)
x[2 + M] += 0.25 * delta_j * (KE - kbT)
x[2 + M] *= np.exp(-0.125 * delta_j * x[3 + M] / Q)
for m in range(3 + M, 2 * M + 1, 1):
x[m] *= np.exp(-0.125 * delta_j * x[m + 1] / Q)
x[m] += 0.25 * delta_j * (x[m - 1] ** 2 / Q - kbT)
x[m] *= np.exp(-0.125 * delta_j * x[m + 1] / Q)
x[-1] += 0.25 * delta_j * (x[-2] ** 2 / Q - kbT)
x[1] *= scale
return x
def A(x):
return U_0 * (x ** 2 - a ** 2) ** 2 / (a ** 4) - 0.5 * ((Lambda * x) ** 2) / k
def U(x, y):
return U_0 * (x ** 2 - a ** 2) ** 2 / (a ** 4) + 0.5 * k * y ** 2 + Lambda * x * y
def F_x(x, y):
return -4 * U_0 * x * (x ** 2 - a ** 2) / (a ** 4) - Lambda * y
def F_y(x, y):
return -k * y - Lambda * x
#-------- The below is the code --------#
# Analytical result
grids = np.linspace(-2,2,25)
grids2 = 0.5 * (grids[:-1] + grids[1:])
A_ana = A(grids2)
A_ana -= np.min(A_ana)
interval = 100
ysamples = []
for i in range(50):
# Update phase space coordinates
for _ in range(100):
X_y = integrateNHC(X_y, weight[1], kbT[1], Q[1])
X_y[1] += 0.5 * dt * F_y(0, X_y[0])
X_y[0] += dt * X_y[1] / weight[1]
X_y[1] += 0.5 * dt * F_y(0, X_y[0])
X_y = integrateNHC(X_y, weight[1], kbT[1], Q[1])
ysamples.append(X_y[0])
print(i,X_y[0])
prob = []
for i in range(len(ysamples)):
commit = []
for _ in range(100):
# Initial coordinates in extended phase space
v_i = np.random.normal(0, np.sqrt(weight * kbT), (M + 1, 2))
X_x = np.zeros(2 * (M + 1))
X_x[1] = v_i[0][0]
X_x[-2:] = v_i[:,0][-2:]
X_y = np.zeros(2 * (M + 1))
X_y[0] = ysamples[i]
X_y[1] = v_i[0][1]
X_y[-2:] = v_i[:,1][-2:]
while True:
X_x = integrateNHC(X_x, weight[0], kbT[0], Q[0])
X_y = integrateNHC(X_y, weight[1], kbT[1], Q[1])
X_x[1] += 0.5 * dt * F_x(X_x[0], X_y[0])
X_y[1] += 0.5 * dt * F_y(X_x[0], X_y[0])
X_x[0] += dt * X_x[1] / weight[0]
X_y[0] += dt * X_y[1] / weight[1]
X_x[1] += 0.5 * dt * F_x(X_x[0], X_y[0])
X_y[1] += 0.5 * dt * F_y(X_x[0], X_y[0])
X_x = integrateNHC(X_x, weight[0], kbT[0], Q[0])
X_y = integrateNHC(X_y, weight[1], kbT[1], Q[1])
if X_x[0] > 1:
commit.append(1)
break
elif X_x[0] < -1:
commit.append(0)
break
prob.append(np.mean(commit))
print(f"{i} / {len(ysamples)}:", np.mean(commit))
plt.hist(np.array(prob), range=(0, 1))
plt.savefig('prob.png')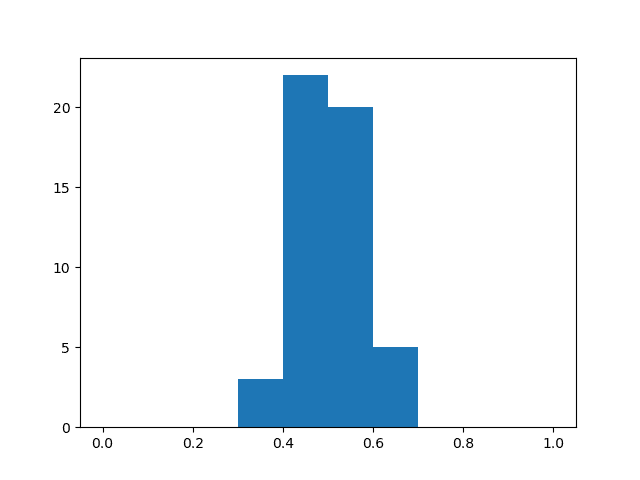

Problem 8.10
$${f(\lambda)=(\lambda^2-1)^4, g=((\lambda-1)^2-1)^4}$$を用いて,図8.2の$${\lambda}$$の自由エネルギープロファイルを生成するための断熱動力学と熱力学積分法のコードをかけ。断熱動力学のパラメータとして,$${k_{\rm B}T_{\lambda}=0.3, k_{\rm B}T=1, m_{\lambda}=250, m=1}$$を採用せよ。残りのパラメータについては,$${\omega_x=1, \omega_y=2,\kappa=1}$$とせよ。
熱力学積分法についてはProblem 8.2で扱ったため省略する。
断熱動力学のpythonによる実装例を以下に示す。
# Import modules
from scipy import integrate
import itertools
import numpy as np
import sys
# Input parameters
N_c = 4 # The number of decompotiosion for the operator exp(i * L_NHC * dt / 2)
weight = np.array([1, 1, 250]) # Atomic weights
M = 2 # The number of chains
Q = 1 # The time scale parameter for all chains
omega = np.array([1, 2]) # Angular velocities
kappa = 1.0 # Coupling constant
kbT = [1, 0.3] # Target temperature
dt = 0.05 # Time step
n_step = 1000000 # The number of replica exchange trials
epsilon = 0.01
# Initial coordinates in extended phase space
x = np.array([0, 0] + list(np.random.normal(0, np.sqrt(weight[:2] * kbT[0]))) + [0,] * M + [np.random.normal(0, np.sqrt(Q * kbT[0])),] * M)
x_L = np.array([0.5, np.random.normal(0, np.sqrt(weight[2] * kbT[1]))] + [0,] * M + [np.random.normal(0, np.sqrt(Q * kbT[1])),] * M)
# Seven weights of the Yoshida scheme for a sixth-order scheme
N_sy = 7
w = [0] * N_sy
w[0] = w[6] = 0.784513610477560
w[1] = w[5] = 0.235573213359357
w[2] = w[4] = -1.17767998417887
w[3] = 1 - 2 * np.sum(w[:3])
# Define functions
def integrateNHC(x, weight, kbT):
dim = len(weight)
for n_c, n_sy in itertools.product(range(N_c), range(N_sy)):
scale = 1.0
KE = np.sum(x[dim:2 * dim] ** 2 / weight)
delta_j = w[n_sy] * dt / N_c
x[-1] += 0.25 * delta_j * (x[-2] ** 2 / Q - kbT)
for m in range(2 * (dim + M - 1), 2 * dim + M, -1):
x[m] *= np.exp(-0.125 * delta_j * x[m + 1] / Q)
x[m] += 0.25 * delta_j * (x[m - 1] ** 2 / Q - kbT)
x[m] *= np.exp(-0.125 * delta_j * x[m + 1] / Q)
x[2 * dim + M] *= np.exp(-0.125 * delta_j * x[2 * dim + M + 1] / Q)
x[2 * dim + M] += 0.25 * delta_j * (KE - dim * kbT)
x[2 * dim + M] *= np.exp(-0.125 * delta_j * x[2 * dim + M + 1] / Q)
scale *= np.exp(-0.5 * delta_j * x[2 * dim + M] / Q)
KE *= np.exp(-1.0 * delta_j * x[2 * dim + M] / Q)
for m in range(2 * dim, 2 * dim + M):
x[m] += 0.5 * delta_j * x[m + M]
x[2 * dim + M] *= np.exp(-0.125 * delta_j * x[2 * dim + M + 1] / Q)
x[2 * dim + M] += 0.25 * delta_j * (KE - dim * kbT)
x[2 * dim + M] *= np.exp(-0.125 * delta_j * x[2 * dim + M + 1] / Q)
for m in range(2 * dim + M + 1, 2 * (dim + M) - 1, 1):
x[m] *= np.exp(-0.125 * delta_j * x[m + 1] / Q)
x[m] += 0.25 * delta_j * (x[m - 1] ** 2 / Q - kbT)
x[m] *= np.exp(-0.125 * delta_j * x[m + 1] / Q)
x[-1] += 0.25 * delta_j * (x[-2] ** 2 / Q - kbT)
x[dim:2 * dim] *= scale
return x
def f(L):
return (L ** 2 - 1) ** 2
def g(L):
return ((L - 1) ** 2 - 1) ** 2
def U(x, L):
U0 = 0.5 * np.sum(weight * (omega * x[0:2]) ** 2)
U1 = kappa * x[0] * x[1]
return f(L) * U0 + g(L) * (U0 + U1)
def F_x(x, L):
F0 = -weight[0:2] * omega ** 2 * x[0:2]
F1 = -kappa * x[0:2][::-1]
return f(L) * F0 + g(L) * (F0 + F1)
def F_L(x, L):
U0 = 0.5 * np.sum(weight[0:2] * (omega * x[0:2]) ** 2)
U1 = kappa * x[0] * x[1]
return -4 * L * (L ** 2 - 1) * U0 - 4 * (L - 1) * ((L - 1) ** 2 - 1) * (U0 + U1)
def A(Lambda):
A_ana = 0.5 * kbT[0] * np.log(weight[0] * weight[1] * (omega[0] * omega[1] * (f(Lambda) + g(Lambda))) ** 2 - (kappa * g(Lambda)) ** 2)
A_ana -= np.min(A_ana)
return A_ana
#-------- The below is the code --------#
grids = np.linspace(0,1,25)
grids2 = 0.5 * (grids[:-1] + grids[1:])
A_ana = A(grids2)
A_ana -= np.min(A_ana)
samples = []
interval = 100
# Equilibrate before sampling
for _ in range(1000):
x = integrateNHC(x, weight[:2], kbT[0])
x_L = integrateNHC(x_L, [weight[2]], kbT[1])
x[2:4] += 0.5 * dt * F_x(x, x_L[0])
x_L[1] += 0.5 * dt * F_L(x, x_L[0])
x[0:2] += dt * x[2:4] / weight[:2]
x_L[0] += dt * x_L[1] / weight[2]
x[2:4] += 0.5 * dt * F_x(x, x_L[0])
x_L[1] += 0.5 * dt * F_L(x, x_L[0])
if ((x_L[0] >= 1 + epsilon) and (x_L[1] > 0)) or ((x_L[0] <= 0 - epsilon) and (x_L[1] < 0)):
x_L[1] *= -1
x = integrateNHC(x, weight[:2], kbT[0])
x_L = integrateNHC(x_L, [weight[2]], kbT[1])
for i in range(n_step // interval):
# Update phase space coordinates
for j in range(interval):
x = integrateNHC(x, weight[:2], kbT[0])
x_L = integrateNHC(x_L, [weight[2]], kbT[1])
x[2:4] += 0.5 * dt * F_x(x, x_L[0])
x_L[1] += 0.5 * dt * F_L(x, x_L[0])
x[0:2] += dt * x[2:4] / weight[:2]
x_L[0] += dt * x_L[1] / weight[2]
x[2:4] += 0.5 * dt * F_x(x, x_L[0])
x_L[1] += 0.5 * dt * F_L(x, x_L[0])
if ((x_L[0] >= 1 + epsilon) and (x_L[1] > 0)) or ((x_L[0] <= 0 - epsilon) and (x_L[1] < 0)):
x_L[1] *= -1
x = integrateNHC(x, weight[:2], kbT[0])
x_L = integrateNHC(x_L, [weight[2]], kbT[1])
samples.append(x_L[0])
prob_num = np.histogram(samples, bins = grids)[0]
A_num = -1 * kbT[1] * np.log(prob_num)
A_num -= np.min(A_num)
dA = abs((A_ana - A_num))
sys.stdout.write(f"\r {(i + 1) * (j + 1):0>6}: {dA.min():.5f} - {dA.max():.5f}, {x_L[0]:.5f}")
sys.stdout.flush()
print("\n")
for c1,c2,c3 in zip(grids2, A_ana, A_num):
print(c1,c2,c3)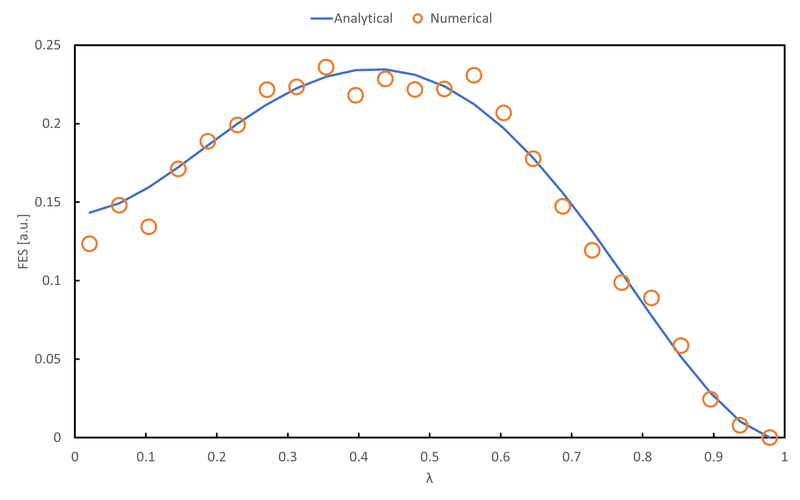
Problem 8.11
(8.10.13)式を導け。
$$
\begin{align*}
\exp({\rm i}\mathcal{L}\Delta t)&=\exp({\rm i}\mathcal{L}_2\Delta t/2)\exp({\rm i}\mathcal{L}_{\rm ref,1}\Delta t)\exp({\rm i}\mathcal{L}_2\Delta t/2)+\mathcal{O}(\Delta t^3)\\
\exp({\rm i}\mathcal{L}_2\Delta t/2)&=\lim_{M\rightarrow\infty}\left[\exp\left(\frac{\Delta t}{4M}\sum_{\alpha=1}^{3N}F_{\alpha}\frac{\partial}{\partial q_{\alpha}}\right)\exp\left({\rm i}\mathcal{L}_{\rm ref,2}\frac{\Delta t}{2M}\right)\exp\left(\frac{\Delta t}{4M}\sum_{\alpha=1}^{3N}F_{\alpha}\frac{\partial}{\partial q_{\alpha}}\right)\right]^M\\
{\rm i}\mathcal{L}_{\rm ref,1}&=\sum_{\alpha=1}^n\frac{p_{\alpha}}{m_{\alpha}'}\frac{\partial}{\partial q_{\alpha}}+{\rm i}\mathcal{L}_{\rm therm,1}(T_q)\\
{\rm i}\mathcal{L}_{\rm ref,2}&=\sum_{\alpha=n+1}^{3N}\frac{p_{\alpha}}{m_{\alpha}'}\frac{\partial}{\partial q_{\alpha}}+{\rm i}\mathcal{L}_{\rm therm,2}(T)\\
{\rm i}\mathcal{L}_{\rm 2}&={\rm i}\mathcal{L}_{\rm ref,2}+\sum_{\alpha=1}^{3N}F_{\alpha}(q)\frac{\partial}{\partial p_{\alpha}}\\
\mathbf{X}&=\begin{bmatrix}q_1&\cdots&q_n\end{bmatrix}^{\rm T}\\
\mathbf{Y}&=\begin{bmatrix}q_{n+1}&\cdots&q_{3N}\end{bmatrix}^{\rm T}\\
\mathbf{P}_{\mathbf{X}}&=\begin{bmatrix}p_1&\cdots&p_n\end{bmatrix}^{\rm T}\\
\mathbf{P}_{\mathbf{Y}}&=\begin{bmatrix}p_{n+1}&\cdots&p_{3N}\end{bmatrix}^{\rm T}\\
\boldsymbol\Gamma_{\mathbf{X}}&=\begin{bmatrix}\eta_{1,1}&\cdots&\eta_{1,M}&p_{\eta_{1,1}}&\cdots&p_{\eta_{1,M}}\end{bmatrix}^{\rm T}\\
\boldsymbol\Gamma_{\mathbf{Y}}&=\begin{bmatrix}\eta_{2,1}&\cdots&\eta_{2,M}&p_{\eta_{2,1}}&\cdots&p_{\eta_{2,M}}\end{bmatrix}^{\rm T}\\
\end{align*}
$$
$${\mathbf{X}}$$の時間発展は$${\exp({\rm i}\mathcal{L}_{\rm ref,1}\Delta t)}$$によってなされる。運動量については$${\exp({\rm i}\mathcal{L}_2\Delta t/2)}$$によって$${\Delta t/2}$$だけ時間発展していることを考慮すると,
$$
\begin{align*}
\mathbf{X}(\Delta t)&=\mathbf{X}_{\rm ref}[\mathbf{X}(0), \mathbf{P}_{\mathbf{X}}(\Delta t/2), \boldsymbol\Gamma_{\mathbf{X}}(0);\Delta t]
\end{align*}
$$
となる。
$${\mathbf{Y}}$$の時間発展は$${\exp({\rm i}\mathcal{L}_{\rm 2}\Delta t/2)}$$によってなされる。
$$
\begin{align*}
\mathbf{Y}(\Delta t/2)&=\mathbf{Y}_{\rm adb}[\mathbf{Y}(0), \mathbf{P}_{\mathbf{Y}}(0), \boldsymbol\Gamma_{\mathbf{Y}}(0),\mathbf{X}(0);\Delta t/2]
\end{align*}
$$
$${\mathbf{Y}(\Delta t/2)\rightarrow\mathbf{Y}(\Delta t)}$$については,その前の演算で$${\mathbf{X}(0)\rightarrow\mathbf{X}(\Delta t)}$$となっていることに注意すると,
$$
\begin{align*}
\mathbf{Y}(\Delta t)&=\mathbf{Y}_{\rm adb}[\mathbf{Y}(\Delta t/2), \mathbf{P}_{\mathbf{Y}}(\Delta t/2), \boldsymbol\Gamma_{\mathbf{Y}}(\Delta t/2),\mathbf{X}(\Delta t);\Delta t/2]
\end{align*}
$$
となる。
$${\mathbf{P}_{\mathbf{Y}}}$$の時間発展は$${{\mathbf{Y}}}$$と同様に表すことができる。
$$
\begin{align*}
\mathbf{P}_{\mathbf{Y}}(\Delta t/2)&=\mathbf{P}_{\mathbf{Y},{\rm adb}}[\mathbf{Y}(0), \mathbf{P}_{\mathbf{Y}}(0), \boldsymbol\Gamma_{\mathbf{Y}}(0),\mathbf{X}(0);\Delta t/2]\\
\mathbf{P}_{\mathbf{Y}}(\Delta t)&=\mathbf{P}_{\mathbf{Y},{\rm adb}}[\mathbf{Y}(\Delta t/2), \mathbf{P}_{\mathbf{Y}}(\Delta t/2), \boldsymbol\Gamma_{\mathbf{Y}}(\Delta t/2),\mathbf{X}(\Delta t);\Delta t]\\
\end{align*}
$$
$${\mathbf{P}_{\mathbf{X}}}$$が$${\mathbf{P}_{\mathbf{Y}}}$$と比較して十分に遅い運動となるため,平均力を用いて時間発展を計算できると考えると,
$$
\begin{align*}
P_{\mathbf{X},\alpha}(\Delta t/2)&\simeq P_{\mathbf{X},\alpha}(0)+\frac{\langle F_{\alpha}\rangle}{m_{\alpha}'}\frac{\Delta t}{2}\\
&=P_{\mathbf{X},\alpha}(0)+\left(\frac{\Delta t}{2m_{\alpha}'}\right)\frac{2}{\Delta t}\int_0^{\Delta t /2}{\rm d}t F_{\alpha}[\mathbf{X}(0),\mathbf{Y}_{\rm adb}[\mathbf{Y}(0),\mathbf{P}_{\mathbf{Y}}(0),\boldsymbol\Gamma_{\mathbf{Y}}(0),\mathbf{X}(0);t]]
\end{align*}
$$
となる。
$${\mathbf{P}_{\mathbf{X}}(\Delta t/2)\rightarrow\mathbf{P}_{\mathbf{X}}(\Delta t)}$$についても同様にして,
$$
\begin{align*}
P_{\mathbf{X},\alpha}(\Delta t)&=P_{\mathbf{X},\alpha}(\Delta t/2)+\left(\frac{\Delta t}{2m_{\alpha}'}\right)\frac{2}{\Delta t}\int_0^{\Delta t /2}{\rm d}t F_{\alpha}[\mathbf{X}(\Delta t),\mathbf{Y}_{\rm adb}[\mathbf{Y}(\Delta t /2),\mathbf{P}_{\mathbf{Y}}(\Delta t /2),\boldsymbol\Gamma_{\mathbf{Y}}(\Delta t /2),\mathbf{X}(\Delta t);t]]
\end{align*}
$$
と計算される。
Problem 8.12
(8.8.22)式を出発点として,積分点$${\{q_i\}}$$における自由エネルギー微分$${{\rm d}A/{\rm dq}_i}$$を得るための加重ヒストグラムの手順を開発せよ。$${A_{k}}$$を求めるためのWHAM法との違いを述べよ。
$$
\begin{align*}
\frac{{\rm d}A}{{\rm d}q^{(i)}}&=\sum_{k=1}^{n_w}C_k\left(q^{(i)}\right)\left.\frac{{\rm d}A_k}{{\rm d}q}\right|_{q=q^{(i)}}
\end{align*}\tag{8.8.22}
$$
各umbrella windowにおいて平均$${\bar{q}_k}$$と分散$${\sigma_k^2}$$を計算する
自由エネルギープロファイルの積分点$${q^{(i)}}$$を決める
$${C_k(q^{(i)})=\tilde{H}_k(q^{(i)})/\sum_{j=1}^{n_w}\tilde{H}_j(q^{(i)})}$$を計算する
$${\frac{{\rm d}A}{{\rm d}q^{(i)}}=\sum_{k=1}^{n_w}C_k(q^{(i)})\{\frac{1}{\beta\sigma_k^2}(q-\bar{q}_k)-\kappa(q-s^{(k)})\}}$$を計算する
$${\frac{{\rm d}A}{{\rm d}q^{(i)}}}$$を数値積分して$${A(q)}$$を求める
WHAM法と異なり,自己無撞着解を得るための繰り返し計算が必要ない。
Problem 8.13
この問題では,分配関数の積分変数の単純な変換が拡張サンプリング法を生成するために利用できることを例証する。この手法は2002年にZhuらによって最初に導入され,2007年にMinaryらによって拡張された。
以下の二重井戸ポテンシャルを考える。
$$
\begin{align*}
U(x)&=\frac{U_0}{a^4}\left(x^2-a^2\right)^2
\end{align*}
$$
配置分配関数は
$$
\begin{align*}
Z(\beta)&=\int{\rm d}x{\rm e}^{-\beta U(x)}
\end{align*}
$$
で与えられる。
a. 変数変換$${q=f(x)}$$を考える。逆関数$${x=f^{-1}(q)=:g(q)}$$が存在すると仮定する。このとき,分配関数が以下の形式
$$
\begin{align*}
Z(\beta)&=\int{\rm d}q{\rm e}^{-\beta \phi(q)}
\end{align*}
$$
で表現できることを示し,ポテンシャル$${\phi(q)}$$の具体的な表式を与えよ。
b. 次に以下の変換を考える。
$$
\begin{align*}
q&=f(x)&=\begin{cases}
\int_{-a}^x{\rm d}y{\rm e}^{-\beta \tilde{U}(y)} &\text{if } -a\leq x\leq a \\
x &\text{if } |x| > a
\end{cases}
\end{align*}
$$
$${\tilde{U}(y)}$$は連続関数であると仮定する。この変換はspatial-warping 変換として知られている(Zhu et al., 2002; Minary et al., 2007)。$${f(x)}$$が$${x}$$に対して単調増加関数である(=$${f^{-1}(q)}$$が存在する)ことを示せ。この変換によって得られる分配関数の表式を書き下せ。
c. $${\tilde{U}(x)}$$を
$$
\begin{align*}
\tilde{U}(x)&=\begin{cases}
U(x) &\text{if } -a\leq x\leq a \\
0 &\text{if } |x| > a
\end{cases}
\end{align*}
$$
に選んだ場合,$${\phi(x)}$$は単井戸型のポテンシャルエネルギー関数となる。$${q\ {\rm vs.}\ x}$$をプロットし,$${x}$$の関数としての$${\phi(x)}$$と$${q}$$の関数としての$${\phi(g(q))}$$を比較せよ。
d. それゆえ,$${\phi(q)}$$を基に実行したモンテカルロ計算,もしくはハミルトニアン$${H(q,p)=p^2/2m+\phi(q)}$$を用いて実行された分子動力学計算は,$${U(x)}$$を直接使用した1つの以上の高いバリアを有するモンテカルロor分子動力学に対する拡張サンプリングのアルゴリズムとなること,及び得られる平衡状態や熱力学的な性質は同一となることを論ぜよ。
ヒント:$${q\ {\rm vs.}\ x}$$のプロットから,$${q}$$の微小変化が$${U(x)}$$の井戸間を移動するくらいの$${x}$$の変化となることに着目せよ。
e. 以下の分布関数をサンプリングするためのモンテカルロ法を考案せよ。
$$
\begin{align*}
P(q)&=\frac{1}{Z}{\rm e}^{-\beta\phi(q)}
\end{align*}
$$
f. 微分の連鎖律$${({\rm d}U/{\rm d}x)({\rm d}x/{\rm d}q),({\rm d}\tilde{U}/{\rm d}x)({\rm d}x/{\rm d}q)}$$を用いて$${q}$$に及ぼされる力の完全な表現を含んだ分子動力学の運動方程式を導出し,これらの力を数値計算するための方法を開発せよ。
ヒント:$${\exp[-\beta\tilde{U}(x)]}$$をルジャンドル多項式$${P_l(\alpha(x)), \alpha(x)\in[-1,1]}$$のような直交多項式を用いて展開することを考えよ。$${\alpha(x)}$$はどのような関数となるべきか?
a.
$$
\begin{align*}
Z(\beta)&=\int{\rm d}q\frac{{\rm d}g}{{\rm d}q}\exp\left[-\frac{\beta U_0}{a^4}\left\{g^2(q)-a^2\right\}^2\right]\\
&=\int{\rm d}q\exp\left[-\beta\left(\frac{U_0}{a^4}\left\{g^2(q)-a^2\right\}^2-\frac{1}{\beta}\ln\frac{{\rm d}g}{{\rm d}q}\right)\right]\\
&=\int{\rm d}q{\rm e}^{-\beta \phi(q)}\\
\therefore \phi(q)&=\frac{U_0}{a^4}\left\{g^2(q)-a^2\right\}^2-\frac{1}{\beta}\ln\frac{{\rm d}g}{{\rm d}q}
\end{align*}
$$
b.
$$
\begin{align*}
\frac{{\rm d}f(x)}{{\rm d}x}&=\begin{cases}
{\rm e}^{-\beta \tilde{U}(x)} &\text{if } -a\leq x\leq a \\
1 &\text{if } |x| > a
\end{cases}\\
&>0
\end{align*}
$$
より,$${f(x)}$$は単調増加関数である。
分配関数は以下の表式で与えられる。
$$
\begin{align*}
Z(\beta)&=\int_{-\infty}^{-a}{\rm d}q{\rm e}^{-\beta U(q)}+\int_{0}^{\int_{-a}^a{\rm d}y{\rm e}^{-\beta\tilde{U}(y)}}{\rm d}q{\rm e}^{-\beta \{U(g(q))-\tilde{U}(g(q))\}}+\int_{a}^{\infty}{\rm d}q{\rm e}^{-\beta U(q)}
\end{align*}
$$
c. $${\beta U_0=5, a=1}$$とした場合の$${x=g(q)}$$の振る舞いを下図に示す。


d. $${\phi(q)}$$には$${U(x)}$$と異なりポテンシャル障壁がないため,重要な区間に対して自由粒子のようなサンプリングが実現される。逆関数の存在$${x=g(q)}$$が保証されているため,$${q}$$のサンプリング値を$${x}$$に変換することが常に可能であるため,$${x}$$空間における解析量を$${q}$$のサンプリングから算出することができる。
e. ランダム変数$${\xi\in[0,1]}$$を生成し,新しい座標候補$${q'}$$を
$$
\begin{align*}
q'&=q+(\xi-0.5)*\Delta
\end{align*}
$$
とする。
受容確率を$${P_{\rm accep}={\rm min}[1, \exp(-\beta(\phi(q')-\phi(q)))]}$$とする。
f. 略。興味ある方は参考文献2を参照のこと。
Problem 8.14
反応座標$${q(\mathbf{r})}$$のコミッター確率$${p_{\mathcal{B}}(\mathbf{r})}$$が関数$${\pi_{\mathcal{B}}(q(\mathbf{r}))}$$で近似できる(=$${q(\mathbf{r})}$$を介してのみ$${\mathbf{r}}$$に依存する)ことが2007年にPetersらによって提案された。
a. この近似の利点と欠点はなんであるか?
b. $${\pi_{\mathcal{B}}(q(\mathbf{r}))}$$が以下の関数形で正確にフィッティングできるとする。
$$
\begin{align*}
\pi_{\mathcal{B}}(q(\mathbf{r}))&=\frac{1+\tanh(q(\mathbf{r}))}{2}
\end{align*}
$$
$${q(\mathbf{r})}$$は良い反応座標であるか否かを理由を含めて述べよ。
a. この近似で上手くいく場合は解釈や扱いが容易になる利点があるが,目的にかなった$${q(\mathbf{r})}$$を定義できるとは限らない。原理的に1つの$${q(\mathbf{r})}$$で反応を記述することができない場合があることも想定される。
b. $${\pi_{\mathcal{B}}(q(\mathbf{r}))=1/2}$$となる点が1つのみであり,単調増加関数であるため,良い反応座標であると言える。
参考文献
Mark Tuckerman, Statistical Mechanics: Theory and Molecular Simulation (Oxford Graduate Texts)
Minary et al., SIAM J. SCI.COMPUT. Vol. 30, No. 4, pp. 2055–2083
この記事が気に入ったらサポートをしてみませんか?
