商群が分かると、群の準同型定理が自然と分かるという話
群の準同型定理は群を学び始めた人が大きくつまずく1つのポイントではないかと思います。教科書を見るとかなり抽象的な内容で書かれていてなんのことだかさっぱり。僕も当初全く意味がわかりませんでした。しかしどうも諦めがつかず、コツコツ考え続けていたら、そもそも商群のことを完全に理解できていないことが準同型定理の理解を妨げていることに気づき、商群ひいては正規部分群がいかなるものなのかをきちんと理解することで、ついに準同型定理を証明することができました。
この投稿では自分の備忘録も兼ねて、準同型定理を理解するまでに必要な道程を順々にゆっくり書いていければなと思います。
この投稿の方針
この投稿は商群や正規部分群、自然な写像の理解がイマイチで、準同型定理の理解に苦しんでいるという方に向けた記事です。なので、そもそもそれらは分かっているけど、他の理由で群の準同型定理がわからないという人にはミスマッチな内容となるかと思います。特に自然な写像は準同型定理の核心とも呼べるもので、自然な写像の理解には商群の理解が必要不可欠です。この投稿では商群と自然な写像の関係性を理解し、群の準同型定理(第一同型定理)を「感覚的に理解する」ことを目指します。
また、「感覚的に理解する」という話なので、細かい証明は割愛することが多々あります。諸々の細かい証明が知りたい方は、群論に関するレポート
https://github.com/noppoMan/math-report/blob/master/group/group.pdf
も適宜参照してみてください。なお、同値関係および、写像、群の基礎-準同型までは理解できているものとして進んでいきます。
同値類の復習
商群や自然な写像に入る前に、まずは同値類について復習していきます。
ある集合Sの元が同値関係を持つとき、この集合Sは同値類と呼ばれます。
群の準同型定理では、同値関係を合同関係と見なします。合同関係とは、ある整数aとbをある整数mで割ったときの余りが等しい場合に成り立つ関係です。例えば、5と11は3で割ると余りが2となり、数学的には3を法として5と11は合同であると言い、5 ≡ 11 (mod 3)と書きます。(もちろんこの合同関係は同値関係ですので、推移律、対称律、反射律を満たします。)
今は3で5と11を割ったわけですが、これを整数全体に適用することを考えます。整数全体を3で割るわけですから
・余り0 (割り切れる)
・余り1
・余り2
の3つのグループに過不足無く分けることができます。
つまり、余り0, 1, 2となる整数の集合をそれぞれ、
・余りが0となる整数の集合: {x ∈ Z | 3x+0 ∈ Z}
・余りが1となる整数の集合: {x ∈ Z | 3x+1 ∈ Z}
・余りが2となる整数の集合: {x ∈ Z | 3x+2 ∈ Z}
(Zは整数全体)
と表すことができます。これは、整数の集合を3等分したと言えます。ここで、各グループの元はそれぞれが合同関係を満たしているため、これら3つのグループはそれぞれが同値類です。そして、群ではこれらの同値類のことを剰余類と言い、剰余類の代表元xにオーバーラインを付けて
![]()
と書きます。noteではtexがサポートされていないので、オーバーラインが表記できません。そのため、以後はもうひとつの書き方である[x]で剰余類を表記します。
これらをさらにひとつの集合にまとめた集合族が商集合Z/nZであり、3で割った場合はZ/3Zと表します。Z/3Zは以下のような集合です。
Z/3Z = { [0], [1], [2] }
この集合の相対的な大きさを指数と言い、Z/3Zの指数は3です。Z/5Zなら指数5ですね。
[0], [1], [2]のそれぞれがZの部分集合になっているので、Z/3ZはZの冪集合の部分集合になってます。
ここからは、準同型定理の証明のため、Z/3Zが群の性質を備えているかを見ていきます。
商集合Z/3Zが群として扱えるためには演算が定義される必要があるわけですが、加法を例に見ていきましょう。
Z/3Zの代表元[0], [1], [2]は、それぞれ3x, 3x+1, 3x+2という形をしています。3xであれば、0, 3, 6, 9, ...の3の倍数、3x+1は3xの元に1を足しているわけですから、1, 4, 7, 10,....、同様にして3x+2は2, 5, 8, 11, ....となるのが分かるかと思います。
ここで、この剰余類の代表元どうしを試しに足し合わせてみましょう。
例えば、10 + 9 = 19を使うとおもしろいことがわかります。この19は実は 3x+1の剰余類に属する数なので、19 ≡ 1となることが合同関係から分かります。つまり、10 ≡ 1、9 ≡ 0なので、10 + 9 ≡ 1 + 0 ≡ 1という関係が成立し、両端ともに、[1]に属するということが分かります。これは積でも同様のことが成り立ちます。(確かめてみてください。)
つまり、一般的には
[a] + [b] ≡ [a + b]
[a] × [b] ≡ [a × b]
(a, b ∈ Z)が成り立ちます。
この関係式より、[1]と[0]の間の加法を[1] + [0] = [1 + 0](=[1])のように定義することができます。これは合同関係を持つ同値類どうしの演算なので、[10] + [9]を[1] + [0]や[22] + [-21]と演算したときも、これらの演算結果の同値類は同じになることを意味しています。つまり
[10 + 9] = [1 + 0] = [22+ (-21)] = [1]
が成立するのです。代表元の選び方を変えれば同様のことが[0],[2]でも言えます。(確かめてみてください。)
さらに着目してほしいのは、[0]が単位元のように振る舞っているということです。つまり、[1 + 0] = [1]となっているのです。[0]は単位元として扱うことができるんですね。あとは、すべての[x]に逆元が存在すれば、Z/3Zは加法において群とみなすことができそうです。逆元は簡単に選び出せます。[x]に対して、[-x]を選ぶと、[x] + [-x] = [0]となり単位元となります。[0]は3Z + 0であったわけですから、[0] = 3Zであることも確認できます。
以上より、Z/3Zは加法において群であるということが分かります。
乗法に関してはやや複雑なのですが、一般の群と同様に[0]を抜き、[1]を単位元とすることで群となります。
これを一般化すると
[a] + [b] = [a + b]
[a] × [b] = [a × b]
のように、合同式における加法と乗法を[a]、[b]間の演算として拡張できるということです。
また、同値類どうしの演算では、ある代表元x ∈ [a], y ∈ [b]を[x] + [y]としても、結局その演算結果は、[a + b]あるいは他の異なる代表元として表せてしまいました。(乗法でも同様です。)
これは、同値類の加法と乗法は、任意の代表元による加法と乗法により自然に定まるということであり、代表元の選び方によって演算結果が変わることがない = well-definedであるということが保証されていることを意味します。これらより、Z/3Zは二項演算に閉じていて、群の性質を満たすため、群であることが分かったのです。
Z/3Zの一般化を目指す
ここからは、一般的な群Gにも、上で示した合同関係とその演算を持ち込めるか考えていきましょう。
集合Gを演算*で群とします。単位元はeです。
群Gが合同関係を満たすためには、
a, b, c, d ∈ G,
a ≡ b, c ≡ d, ・・・・(ⅰ)
a * c ≡ b * d
が言えればいい訳ですから、この合同関係が成り立つようなケースを考えていきましょう。
3を法とした整数の合同式では、a ≡ bは本質的には、a - b ∈ 3Zと言えます。言い換えると、aとbの差が3Zの元になるということです。3の倍数とは3Zの元ですから、一般の群も同様に過不足無くグループ分けした場合、3Zのように振る舞う部分群があると考えるのが良さそうです。そこで、そのような部分群をNと仮定し、試しにGをNで割り有限個の剰余類を元とする群を構成してみましょう。それは、G/N = {[e], [a1], [a2], [a3], ...[an]} です。この時[e]は単位元です。Z/3Zのとき、3Z = [0]は単位元でしたね。よって、G/Nでは、N = [e]と考えることもできます。
次に、演算を導入していきます。Nは今、部分群と仮定されていました。Nが部分群であれば、Gの演算*をNに適用することができます。
g ∈ Gに対し、g*H = {g*h | h ∈ H}を定義します。
同様に、右からgを作用させたH*g = {h*g | h ∈ H}も定義します。
一般に、群は非可換として考えますから、このように左右から*を適用する演算を考えています。
この定義により、剰余類における補題
Gを群、Hをその部分群とするとき、g ∈ H <=> g*H = H <=> H*g = H
が使えるようになりましたので、G/Nでも成立するか確認してみます。
NをHとします。g ∈ Nに対し、g*Nを行うと、単位元Nに属する代表元gも結局はNと表すことができますから、g*N = Nとなります。同様にgを右から作用させてもNとなり、G/Nでもこの補題が成り立ちます。
次に、同値関係を導入してみましょう。
g, g' ∈ Gに対し、同値関係「~」をgN = g'Nのとき、g ~ g'であると定義します。
このとき、g ~ g' <=> g'^{-1}*g ∈ Nです。
この演算と同値関係の定義により、(ⅰ)を満たすことができます。(合同関係の関係式がwell-definedであることはすでに示しました。)
そして、この関係を満たすと部分群の必要十分をも満たします。
■部分群の必要十分条件
・e ∈ H
・x, y ∈ H ならば、xy ∈ H
・ x ∈ H ならば、x^{-1} ∈ H
つまり同値関係とその演算が成り立てばNはGの部分群になるので、仮定は正しいということになります。
ここまでで、もうひとつの解決しなければいけない大きな疑問が残っています。
それは、GはNで割れるのかということです。
Z/3Zの例では、Zを3Zで割って、Zを3つの剰余類のグループに分けていたわけですが、Zはなぜ3Zで割ることができたのでしょうか?
その理由が正規部分群にあるのです。
正規部分群と商群
■正規部分群の定義
H を群 G の部分群とする。H が G の正規部分群であるとは、すべての g ∈ G に対し gHg^{-1} = H が成り立つことである。
これが正規部分群の定義です。これはつまり、すべてのg ∈ Gに対して、ghg^{-1} ∈ H (h ∈ H)ということです。これをZ/3Zで考えると、任意のg ∈ Zに対して、g+h+g^{-1} ∈ 3Z (h ∈ 3Z)が成り立つことが分かかります。もうすこし簡単に言うと、すべてのgとgの逆元を足すとゼロになり,そこに3の倍数を足したら3の倍数なので3Zになりますね。(上で加法を使ったのでここでも加法にしています。)よって、3Zは正規部分群であることが分かります。
つまり、Hが正規部分群であれば、Hの元の違いを同一視あるいは無視することで、Gの元を同一視できるということを言っています。
(よくHが正規部分群なら、左剰余類と右剰余類が一致するという命題を目にすると思いますが、それは両辺が非可換であってもHの元を同一視することで可換に相当するような振る舞いを見せるということです。)
ここで仮に、Hの元の違いを同一視できないとすると、代表元の選び方によってこの演算結果は変わってしまい、常に`gHg^{-1} = H`を示すことはできなくなります。
合同関係であれば、a, b, c, d ∈ G/Hに対して、
ある時点で[a] = [b], [c] = [d]だとしても、いずれかの代表元を変えることで、[a + c] ≠ [b + d]が導かれてしまい(ⅰ)に反してしまうのです。
以上のことから、正規部分群HでGを割るということが非常に重要である事がわかりました。この正規部分群HでGを割ったG/Hを商群といいます。
つまり、一般の群でも正規部分群で元の群を割ることで、商群を構成できるということです。
自然な写像
商群の成り立ちを理解したところで、ついに冒頭にもあった自然な写像について考えることができるようになりました。
f: G -> G/Hが準同型写像である時、π: G -> G/ker(f)となるπを自然な写像と定義しました。
ker(f)について軽くおさらいをすると、fが準同型である時、
{ x ∈ G | f(x) = e} となるような部分群を群のカーネルといいker(f)と書きました。(eは単位元) また、準同型写像の命題でカーネルはfの正規部分群であることの証明を目にしたことがあるかと思います。つまり、G/Ker(f)は商群だったのです。
ここで、今一度Z/3Zに立ち返って見ましょう。鋭い人はピンと来たかもしれませんね。3Z = [0]なので、φをZからZ/3Zへの準同型写像とすると、
φのカーネルは
ker(φ) = {x ∈ Z | φ(x) ∈ [0]} = 3Z
となるのです。脳汁が出ますよね。
つまり、φのカーネルは3Zだったのです。
これより、自然な写像をπ'とすると、φとまったく同様に
ZからZ/3Z = Z/Ker(φ)への準同型写像となるのです。
ここまで理解が進んだらもう準同型定理の可換図式がクリアに見えますよ。
群の準同型定理(第一同型定理)を紐解く
改めて、準同型定理(第一同型定理)の主張と可換図式を見てみましょう。
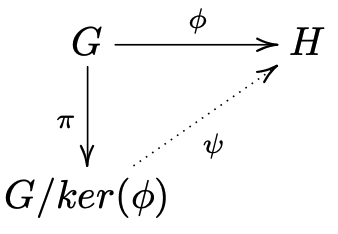
これは準同型定理の可換図式です。準同型定理の主張は、ψが同型であるというものです。
難しい証明は置いておき、Z/3Zの例でKer(φ)が実は3Zであったことを考えると今の私達の目には、この可換図式は以下のように見えるでしょう。
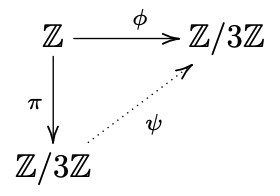
Z/3ZからZ/3Zへの写像は自分自身から自分自身への写像なので、明らかに全単射かつ同型であることがすぐに分かるかと思います。
このように、同値類、正規部分群、商群ときちんと段階を踏んで理解することで準同型定理はこんなに簡単にイメージすることができるのです。
ここでは準同型定理の細かい証明はしませんが、冒頭で挙げた群のレポートの最後に準同型定理の一般的な群における証明をしていますので、興味がある方は覗いてみてください。
またこの記事を書くに当たり、データサイエンティストであり、理学修士の吉田智哉(reonalab.org)さんにレビューいただきました。非常に細かいニュアンスのご指摘をいただき、僕自身準同型定理に関してさらに理解が深まりました。限られたお時間の中で丁寧なレビューありがとうございました。
この記事が気に入ったらサポートをしてみませんか?
