ミニゲーム　「雲歩き算」　研究

このゲームは、非負整数の X軸上で行う

まず　ボードサイズを決める。
最小のボードサイズは bit_p = 2。
bit_p の bit の由来は 「0 か 1 か」 を意味する bit から、
p は 周期（period）の頭文字だ。
左右はループしてつながっていて、右端と左端は同一だ

このあと頻出する用語の説明

このゲームでは、方眼紙を使って　横幅の厚み１以上の　平行四辺形　を描く。
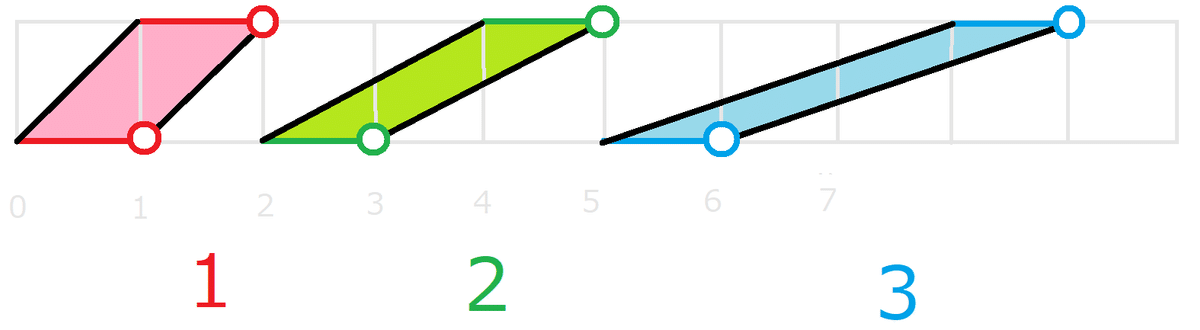
上辺を天、下辺を地、天でも地でもないところを目（め）と呼ぶとする。
目は囲碁用語から借用した。
この平行四辺形の天と地は必ず被らないものとし、
目は　有るときもあれば　無いときもある

さきほどの図を　上から見れば、
X軸は　地、目、天　のいずれかで埋まっていると考えてよい。
目は　空きスペース　で表した

平行四辺形　「毛」

平行四辺形のよく使われる呼び名は
小さな数から順に「a（エー）」「b（ビー）」「c（シー）」とか、
「除去可能数」　と呼ばれるが、

なんだか　呼びづらいので
本書では　「毛（け）」　と呼ぶことにする。
毛の形は　「終点 － 始点」　の差で求めた整数で　表すのが簡単だ

羽

同じ「地」から生えている「毛」の束を
特に名前が無かったから「羽（はね）」と名付ける。
毛は　１つ１つが　バラバラに離れて存在することはなく、
すべて　羽　になっている。
毛の形は整数で表せたから、それをまとめて
S={1,2,3}
と書くのが　羽　の簡単な表し方だ。
S の正式名称は「サブストラクションセット」だが、
長ったらしいので　本書では　羽　と呼ぶ

羽は　飛び番でもいいし、
１つの羽の毛の数は　１個以上なら　いくつでもいい
毛に名前を付けたいなら、数の小さな方から a, b, c, … と付けていく

ゲームルール　羽目張り

天でも　地でもないところを　目と呼ぶと　前に説明した。
すべての目から　「羽」　を生やしてほしい。
「天」は何重かに被ることがあるが、構わない。
そして、「目」を無くしてほしい
（右端に無限に続くスペースは目に含めない）

羽を１つ　生やすだけで　いくつか埋まった

羽を　もう１つ生やすと　これで目は全て埋まった

すると、S={3,5,8} は、
bit_p=11 のようだ

１つ目のミニゲーム

「雲歩き算」を　まだ説明していない。
（多分、既知の前提知識を説明するだけで
　この記事の大半を使うと思うが）
ここで　ミニゲームとして　まとめることで　一息付けることにする。

２以上の任意の数の bit_p を決め、
その bit_p にピッタリ収まる　羽 S={a, b, c…} 　を挙げてほしい。
無限に有ったり、１つも無かったりするから、
いい加減　飽きたところで止めるといいだろう

ここで　せっかくだから、ループについて説明する

ループ

上図　S={1,3}　を見ると
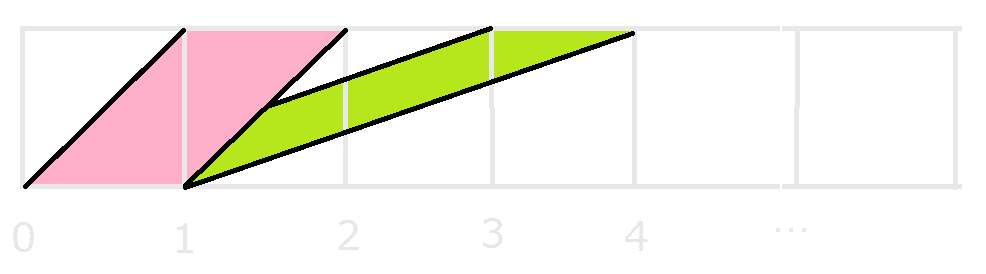
２（と３の間）　が目に見えるが

bit_p=2 と決めてしまえば、
目は無くなる。
S={1,3} は、
bit_p=5 にしても目は消えるが正解ではなく、
最小の bit_p である bit_p=2 だけを
正解とするのが決まりだ

そう考えると
S={1} も
S={1,3} も
S={1,3,5} も
S={1,3,5,7} も
S={1,3,5,7,9} も

bit_p=2 になることが　なんとなくわかると思う
このように　類型（パターン）化　したり、
その条件を見つけたりしてほしい

ここで bit_p （周期）と言っているのは、
地と天だけを見て言っている。

専門的には　名前が付いていなかったり、
bit-grundy数　と呼んだりするようだが
本書では　特に　こだわらない

復習　羽目張り

S={1,5} は、
一見　bit_p=2 には見えないが、 bit_p=2 になる。
なぜなら

羽目張り　が　ルールの中に含まれている　からだ。
しかし　疑問が残るかもしれない

S={1,5} は、羽目張りをすると、また新しい目を作ってしまう
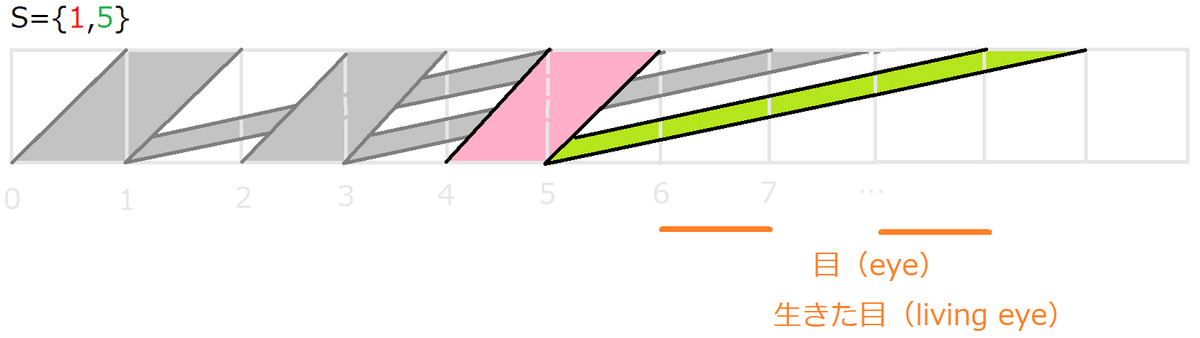
（このような目を　生きた目　とでも呼ぶとしよう）

だから　永遠に　羽目張り　を続ける

普通、停止しない計算は
　計算機としては不具合だが、
数学でも　囲碁でも　無限を扱う方法がある

無限の扱い方の一例

羽目張り　をするのは、目を潰すためだった。

もし、羽目張りをして、
同型の　天、地、目　が２度現れたなら、
無限ループしていると考えてよい。
詳しく見てみよう

地天目天目天　「に、戻った」　と考える。
一方通行の空間で、来た道のどこかに戻ったなら、無限ループしていると考えていい

では、
無限ループしているのなら、どうするだろうか？

よくあるのは　「ルールを変える」　ことだ

この例では　「目」と「生きた目」を区別し、
「生きた目」　には　「羽目張りルール」　を適用しない

これで　「羽目張りルール」　の中に含まれた
自動のしくみ　が終わる

この変更で矛盾なく　無限ループ　「では、なくする」　ことができる。
（無限ループを止めることはできない。無限ループでなくする必要がある）

これで bit_p=2 が求まりそうだ

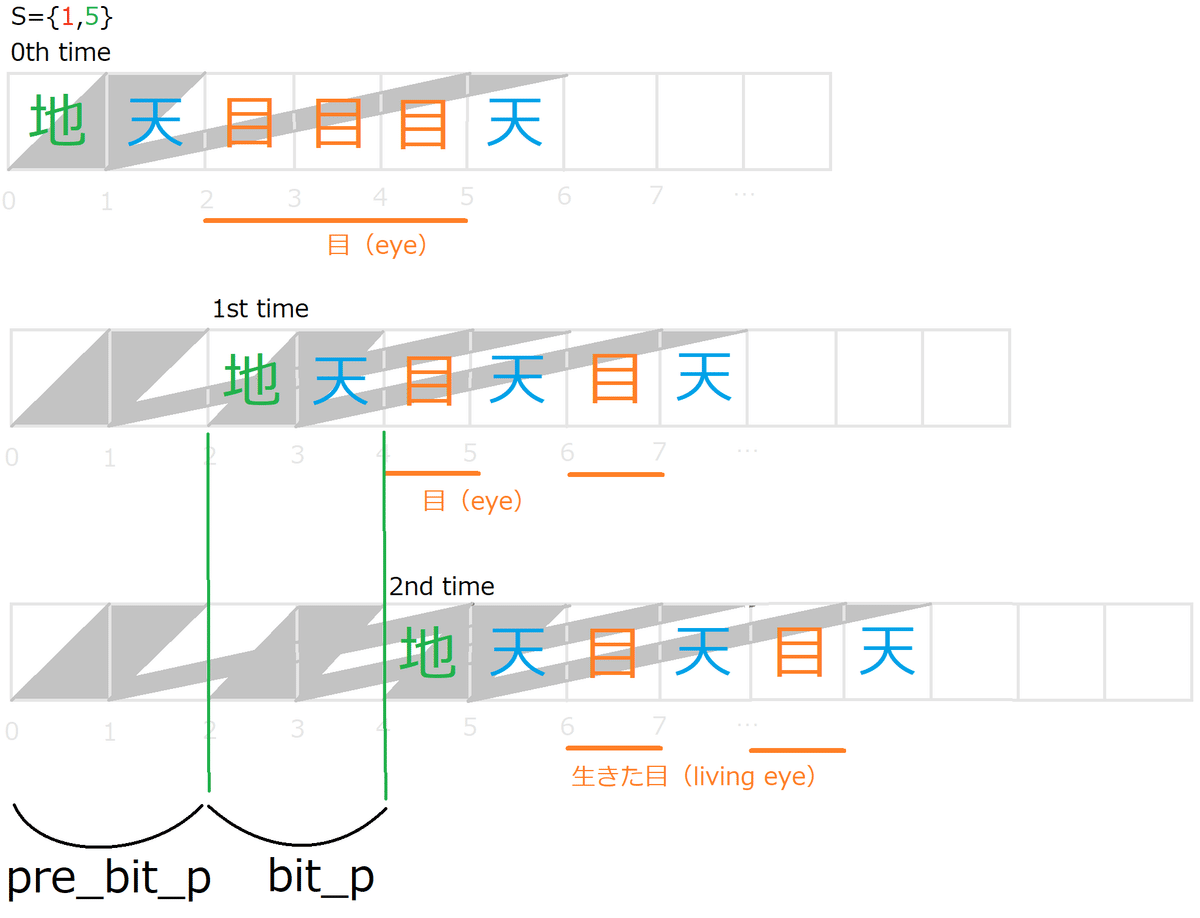
周期より前の部分（pre_bit_p）があるが、
羽目張りルールを止めたときに pre_bit_p が
bit_p の繰り返しで構成されているのと同じに見えるなら
pre_bit_p は無いものと　みなす

つまり、あたかも bit_p から始まったものとして扱う

pre_bit_p が有るケース

S={3,7,8} には pre_bit_p がある。見てみよう

羽を　１本１本　生やすと　めんどうなので
厚みのある平行四辺形にすると便利だ

元からある目を　すべて潰した
新しく　目を２つ作ってしまっているのが見える

２つの目を潰すと、
また新しく　２つの目が作られた

省略するが
ここから先は　繰り返しになるようだ

羽目張り　が止まったところで
pre_bit_p と bit_p を探してみよう

S={3,7,8} のとき、 bit_p=5, pre_bit_p=11 だ。
詳しく見てみよう

「地地天天天」で周期に入っているので、
bit_p は 5 だ。
pre_bit_p は 11 のようだ

pre_bit_p の長さ　や、　bit_p の長さ　を、
羽目張り　（つまりアルゴリズム的な計算、算法）をせずに、
S={a,b,c,…} から計算で求める方法があるのか　わたしは知らない

グランディ数　（p=b+c系）

次に　グランディ数　を説明する

S={1,4,8} とし、
0番地の下側に 0 を置く

S={a,b,c} のように毛に名前を付けよう

a の毛に吸いあげられるように
1番地の上側に 0 を置く

1番地の上側にある数を除く、
最小の非負整数を 1番地の下側に置く

今説明した２行の計算を mex と呼ぶ。
mex は、最小除外数（minimum exclusion）という意味だ

しばらく　同じような　繰り返しが続く

1番地の下側の 1 を まるで aの毛が 吸い上げたかのように
2番地の上側に置く

mex して 2番地の下側に 0 を置く

2番地の 0 を a の毛で吸い上げて
3番地の上側に置く

mex して 3番地の下側に 1 を置く

ここで b の毛 も使えるようになった

0番地の下側の 0 をまるで b の毛が吸い上げたかのように
4番地の上側に置き、
3番地の下側の 1 をまるで a の毛が吸い上げたかのように
4番地の上側に置く

mex して 4番地の下側に 2 を置く

1番地の下側の 1 をまるで b の毛が吸い上げたかのように
5番地の上側に置き、
4番地の下側の 2 をまるで a の毛が吸い上げたかのように
5番地の上側に置く

mex して 5番地の下側に 0 を置く

ここから　少し説明を駆け足にして　時間を進める

mex して 1

mex して 0

mex して 1

mex して 2

mex して 3

mex して 2

mex して 0

ここで、さらに駆け足で見ていく

上側に置いてある数は、
下側に置いてある数を　コピーしているだけだ

下側に置いてある数は、
上側に無い最小の非負整数が置いてあるだけだ

この　卵か先か、鶏が先か　のようなメカニズムは
下側の数が先で、上側の数が後だと言える

下側に置いてある数を　よく見てみると

p = 12
と言えるのだそうだ

p は周期（period）

pre_p の長さ　や、　p の長さ　を、
毛を使った吸い上げや、 mex （つまりアルゴリズム的な計算、算法）
を使わずに、
S={a,b,c,…} から計算で求める方法があるのか　わたしは知らない

隣合いを考えるグランディ数

隣り合うタイルが同じ色にならないように
並べたときの　色　の指定だ

隣というのは、上図の a, b, c のようだ

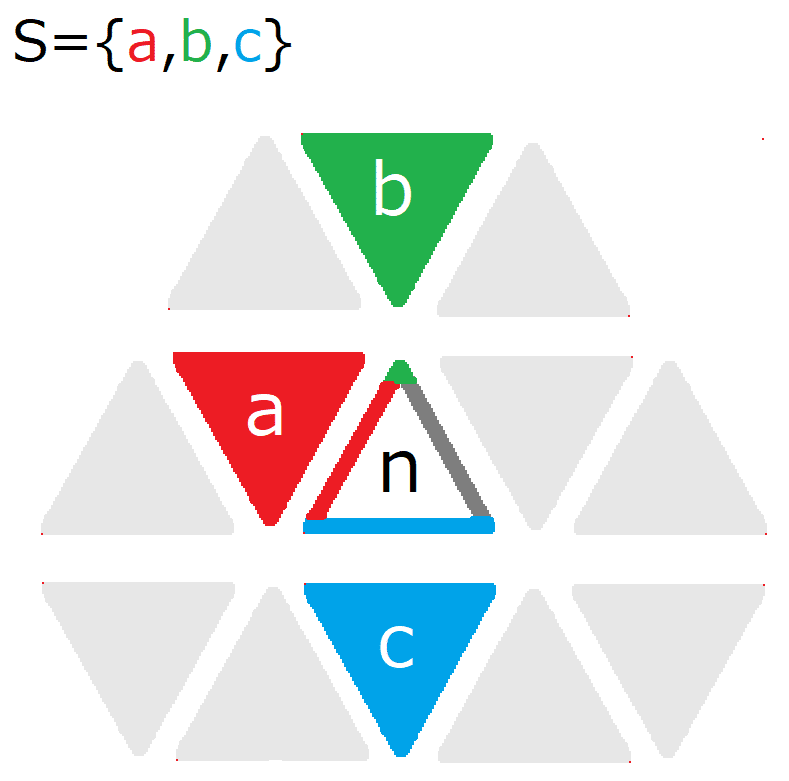
あれっ？　と思うことがある

b が 隣　なのだったら
上図　？　の場所も隣なのかな、と思うが
そうではない

b を無視して
a と c が　「隣」　の感覚を十分満たしているのだから
いいじゃないか

ということかもしれない。
計算において、感覚とピッタリではないが
十分だからいいじゃないか、ということは　よくある

なお　右隣については

次の n が勝手に色を避けてくれるから
考えなくていい

mex とは

隣の色にない色を選ぶしくみだ

毛（bの方）が増えるタイミングにも
うまく対応している

しかし cの毛はどうするのだろう。
未来を指している。
これをどう解決するのか　私には勘が働かなかったが、
イラストレーションを続けると、 mex はそれにも　うまく対応する

Step 8 で １段目に cの毛のための 数列がまた始まるが……

１段目は、４段目でもあるようだ

S={a, b, c} では毛が a と b と c の３本あるが、
これは　上図のテープのようなものが　３本しかないことと
一致するのかもしれない

隣（または向かい）に３色あるとき、４色目が塗られた

グランディ数　（p=c+a系）

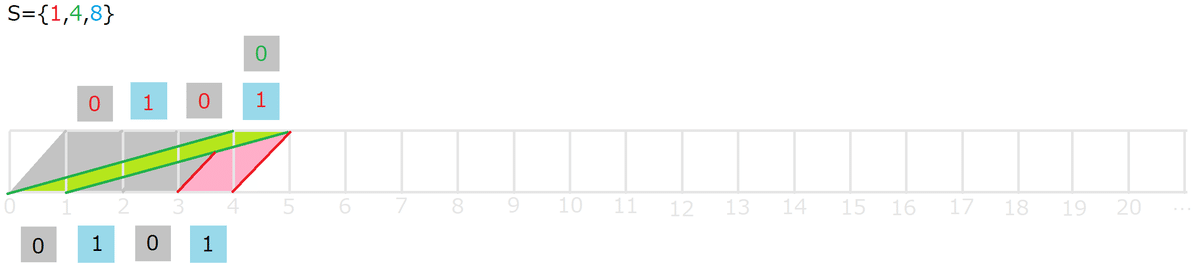
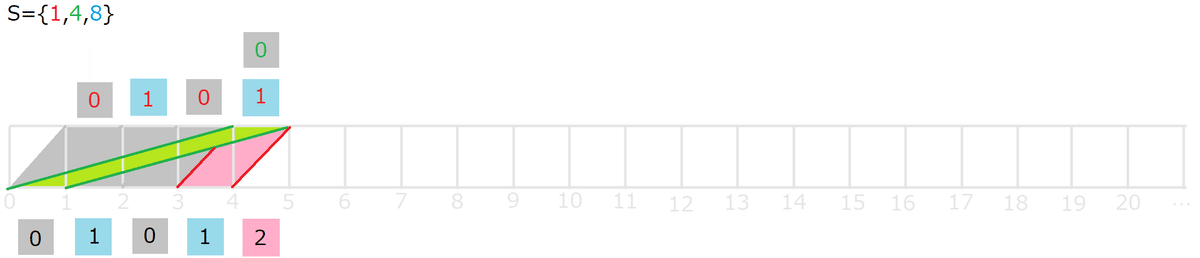
S={1,4,8} は p=b+c=12 だった。
周期は b+c だけではなく、場合分けが数多くある。
次は周期が p=c+a のケースも見てみよう

S={3,4,7} を見てみよう

aの毛が 0番地の下側の 0 を吸い上げて 3番地の上側に置く

0～2番地の上側は何も吸い上げられないので
0 を置いておく

1～2番地の下側は mex せず、
0 を置いておく

mex して 3番地の下側に 1 を置く

mex して 4番地の下側に 1 を置く