
2変数以上の最急降下法について
はじめに
皆さん、こんにちは。
今回は、変数が2つ以上に増えた時に、概念が難しくなる最急降下法について、理解のコツを備忘も含めて記載したいと思います。
最急降下法とは!?
最急降下法は、ある解の探索について、微分の理論を用いながら、効率的に探索する方法になります。
その辺りの説明については、以下の記事にまとめてありますので、もしよければ参照下さい。
変数1つの最急降下法
変数1つの場合、探索指標の値と、探索対象の値との2軸になりますので、図示が簡単です。
その為、最急降下法にて実現していることは、イメージがしやすく明快です。
例えば、以下のような探索の式があったとします。

この式全体の意味は、「2000−300a+a²」という式を E として、その E の値を最小とする変数 a の値を探す、という形になります。
或いは、変数 a を変化させて、E をなるべく小さくする、というミッション付きの式になります。
E をなるべく小さくすることを、最小化といい、min 記号で表します。
min 記号の下に書いてある a は、最小化を行うに当たって、操作する変数の指定となります。
逆に言えば、a 以外は、最小化を行うに当たっても操作しない、という意思表示でもあります。
まあ、ここは式の技術ルールの話です。
或いは、果たしたい目的が最大化である場合は、min 記号の代わりに、max 記号を用います。
そして、最小化や最大化を行うことを、1段上位の抽象表現として、最適化といいます。
最急降下法は、最適化を行う手法の1つとなります。
最小化にも、最大化にも、両方に使用できます。
ちなみに、上記の最小化課題については、以下の式展開によって、E を最小化する a を見つけ出すことができます。

この式変換は、平方完成です。
2次の方程式で、変数が1つであれば、平方完成を行うことで、解の探索が行なえます。
ここで、解とは、E を最小化する a のことですので、a = 20 となります。
何故ならば、上記式において、(a − 20)² は、値が 0 以上となる項である為、この項が 0 である時に、E 式が最小となるのです。
それを実現する a が、20 である訳です。
尚、残る項 1600 は、a の値に依らない定数になります。
最急降下法においても、この解に到達することができます。
最急降下法を行うに当たっては、先ず、E 式を、操作対象の変数 a にて、微分をするところから始まります。
微分については、高校時代に文系だった方などは、触れていないかもしれません。
基本的な考え方については、以下の書籍などを読んでみると良いかと思います。
公式については、以下のサイトなどを参考にすると良いでしょう。
一部については、この記事中でも説明しようと思います。
さて、先程の E 式を微分してみましょう。
以下の微分公式を使えば、実現できます。
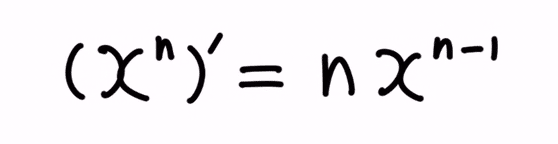
この公式を、各項に対して適用すると、以下となります。
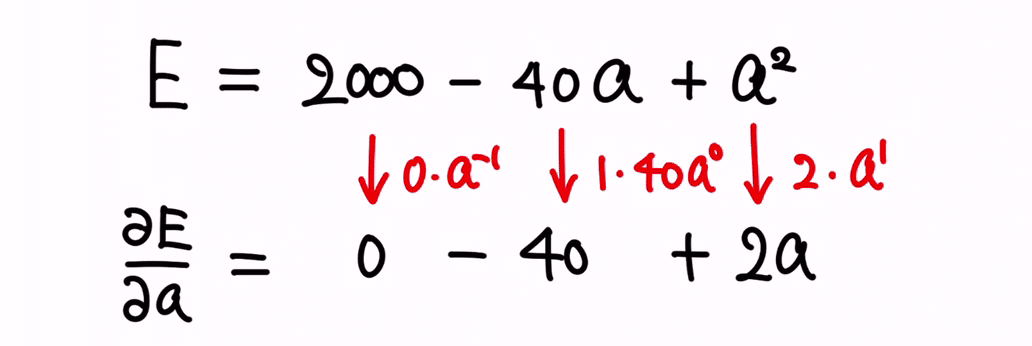
ここで、∂E/∂a とは、E の式を a について微分する、という意味です。
微分式を、E’ という風にダッシュ記号を添えて表すこともあります。
しかし、例えば、E 式の中に a と b の2つの変数があった場合、E’ と記載すると、a について微分しているのか、b について微分しているのか分からなくなってしまいます。
その為、∂E/∂a や ∂E/∂b という風に書く方が、丁寧な表現となります。
E 式の各項を a について微分すると、∂E/∂a が求まります。
尚、∂E/∂a とは、E 式の接線の傾きを表しています。
そして、E は、a についての2次方程式である為、∂E/∂a が 0 である時に、E は最小値をとります。
2次方程式は、必ず凹か凸の形となり山が1つなので、接線の傾きが 0 となる位置が、凹の場合は最小値、凸の場合は最大値となります。
その為、先程の E 式であれば、以下のようにして最小値を求めることもできます。

平方完成で求めた、E を最小にする a = 20 と合致しました。
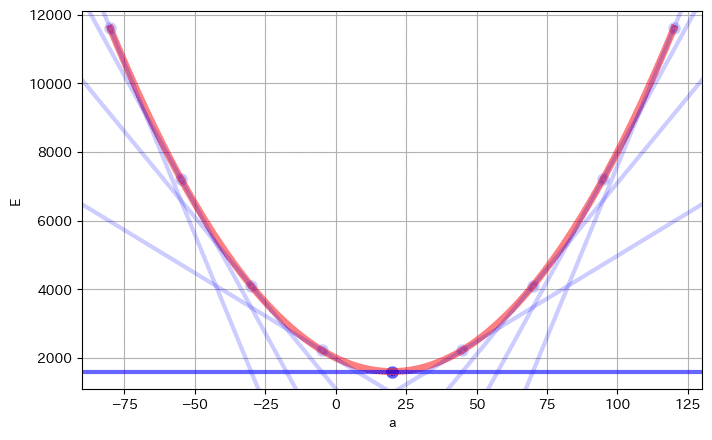
そして、次に、最急降下法ですが、a の初期値を適当に決めて、その場での傾きを求め、傾きを頼りに E が底に落ち込むように、a を求めていく、という形です。
図で、イメージすると以下です。
左から右へと探索しているイメージです。

分かりやすいように、順を追って説明します。
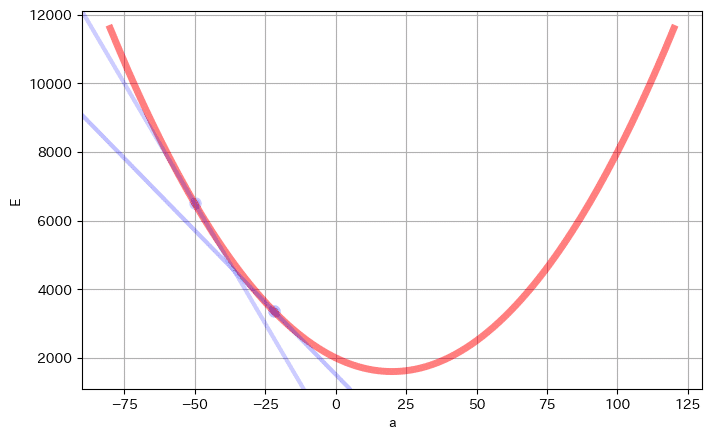
先ず、a の初期値を −50 として、その点の接線の傾きを求めます。

傾きは、∂E/∂a = 2a − 40 で求まります。
その為、a = −50 における、曲線 E = 2000 − 40a + a² の接線の傾きは、∂E/∂a = (2 ✕ −50) − 40 = −140 となります。
最急降下法としては、次のステップとして、傾きを頼りに a を更新します。
今は、曲線の底を目指している最小化ですので、E が小さく方向に a を更新します。
最小化における a を更新する式は以下となります。

η(イータ)は、ある特定の係数を表す文字になります。
アルファベットの h のギリシア文字です。
特定の係数とは、例えば、0.1 等の具体的な値のことです。
最小化を試みる際に、任意に設定します。
η は、大きければ a を積極的に動かすことになり、小さければ a を慎重に動かす形となります。
∂E/∂a は接線の傾きです。
尚、底を目指すべく、a を更新する場合、以下のように動かすべきです。
- 接線の傾きがマイナスである場合、底は、今の a の位置よりも右側にある為、a を右側に動かす
- 接線の傾きがプラスである場合、底は、今の a の位置よりも左側にあるので、a を左側に動かす
つまり、傾きの符号がマイナスならば、a をプラス方向に動かす。
傾きの符号がプラスならば、a をマイナス方向に動かす。
そうして、a を徐々に底に誘導していきます。
尚、a の更新式の符号については、E の式が凹なのか、凸なのかによって、変わります。
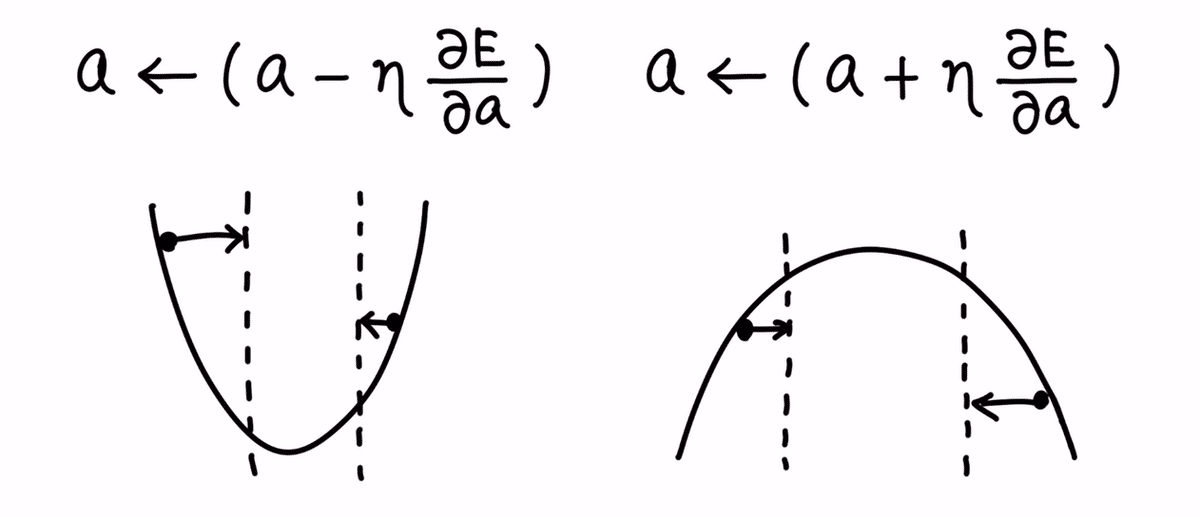
つまり、最小化したいのか、最大化したいのかによって、a の誘導の仕方が逆になる形です。
また、誘導の強さも、傾きの大きさによって変わります。
特に、2次方程式の最小化の場合、底から遠いほど、接線の傾きの絶対値は大きくなっていきます。
∂E/∂a = 2a − 40 である為です。
その為、最小化の挙動として、序盤は誘導が強く、終盤に行くにつれて誘導が弱くなっていく、という傾向となります。
その様子を、先程の a = −50 の初期値のところから見ていきましょう。
尚、a の更新式の η は 0.2 としてみます。
曲線 E = 2000 − 40a + a² の接線の傾きは、∂E/∂a = −140 でしたので、a の更新式は、a ← a − (η ✕ ∂E/∂a) に値を当てはめてみて、a ← a − (0.2 ✕ -140) = a + 28 となります。
つまり、a に 28 を足す更新となり、a = −22 となります。
図でイメージすると以下です。

こんな感じで、a を右に移動させる感じになります。
こうして、a は、晴れて底に近付きました。
次に、a は今、−22 になりましたので、a = −22 における、曲線 E の接線の傾きを求めます。
a = −22 における、曲線 E = 2000 − 40a + a² の接線の傾きは、∂E/∂a = (2 ✕ −22) − 40 = −84 となります。

a = −50 における曲線 E の接線の傾きが −140 から、a = −22 における曲線 E の接線の傾き −84 へと、傾きの絶対値が小さくなっています。
傾きの絶対値が小さくなっているということは、曲線 E の底に近付いている証拠です。
そして、ここでも a を更新します。
曲線 E = 2000 − 40a + a² の接線の傾きは、∂E/∂a = −84 ですので、a の更新式は、a ← a − (0.2 ✕ −84) = a + 16.8 となります。
つまり、a に 16.8 を足す更新となり、a = −5.2 となります。
もう一回だけ、a の更新を追ってみましょう。
a は今、−5.2 になりましたので、a = −5.2 における、曲線 E の接線の傾きを求めます。
a = −5.2 における、曲線 E = 2000 − 40a + a² の接線の傾きは、∂E/∂a = (2 ✕ −5.2) − 40 = −50.4 となります。
そして、a の更新は、曲線 E = 2000 − 40a + a² の接線の傾きは、∂E/∂a = −50.4 ですので、a ← a − (0.2 ✕ −50.4) = a + 10.08 となります。
よって、a に 10.08 を足す更新となり、a = 4.88 となります。

3回の更新を振り返ってみると、以下のようになっていました。

どんどん底に近付いてますね。
また、傾きの大きさ、或いは、底からの遠さに応じて、a の更新が段々小さくなっていることも確認できます。
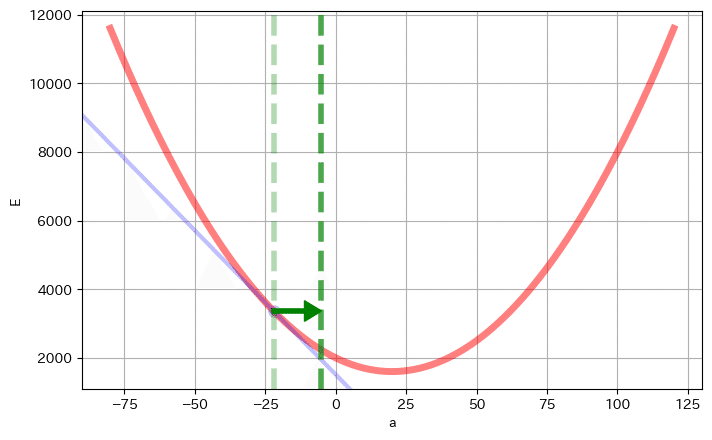
そして、これを更に繰り返して、計10回の更新を行ってみると、以下図のような形になります。

最も濃い緑の縦線位置が、10回繰り返した際の a の位置です。
更新毎の a の値は以下となります。
初期値 : a = −50
1回目の更新 : a = −22
2回目の更新 : a = −5.2
3回目の更新 : a = 4.88
4回目の更新 : a = 10.928
5回目の更新 : a = 14.5568
6回目の更新 : a = 16.73408
7回目の更新 : a = 18.040448
8回目の更新 : a = 18.8242688
9回目の更新 : a = 19.29456128
10回目の更新 : a = 19.576736768
これを30回繰り返すと、a = 19.9999845… となって、ほぼGOALです。
なぜならば、a = 19.9999845… における、曲線 E = 2000 − 40a + a² の接線の傾きは、∂E/∂a = (2 ✕ 19.9999845…) − 40 = −0.000031 ≒ 0 となります。
接線の傾きが、ほぼ 0 になっている為に、E を最小とする a が見つけられていると判断できます。
尚、プログラムは以下となります。
import numpy as np
import matplotlib.pyplot as plt
a = np.arange(-100, 101) + 20
a_ = np.array([-200, 200])
E = (a**2) + (-40 * a) + 2000
plt.figure(figsize=(8, 5), dpi=100)
plt.plot(a, E, color='r', alpha=0.5, linewidth=5)
xlim_tmp = plt.gca().get_xlim()
ylim_tmp = plt.gca().get_ylim()
a_tmp = -50
eta = 0.2
iter_num = 10
for iter_i in range(iter_num):
E_tmp = (a_tmp**2) + (-40 * a_tmp) + 2000
dE_da_tmp = (2 * a_tmp) - 40
alpha_tmp = 0.2 + (0.05 * iter_i)
plt.scatter(a_tmp, E_tmp, color='b', alpha=alpha_tmp, linewidth=3)
plt.plot(a_, ((dE_da_tmp * a_) - (dE_da_tmp * a_tmp) + E_tmp),
color='b', alpha=alpha_tmp, linewidth=3)
a_before = a_tmp
a_tmp = a_tmp - (dE_da_tmp * eta)
print('%d回目の更新:a = %.10f' % ((iter_i+1), a_tmp))
plt.plot([a_before, a_before], ylim_tmp, color='g', alpha=alpha_tmp, linewidth=4, linestyle='dashed')
if (iter_i == (iter_num - 1)):
plt.plot([a_tmp, a_tmp], ylim_tmp, color='g', alpha=0.7, linewidth=4, linestyle='dashed')
plt.plot([a_before, (a_tmp - 2)], [E_tmp, E_tmp], color='g', linewidth=4)
plt.gca().arrow(x=(a_tmp - 3), y=E_tmp, dx=np.pi, dy=0,
head_width=600, head_length=6,
length_includes_head=True, color='g')
plt.grid()
plt.xlim(xlim_tmp)
plt.ylim(ylim_tmp)
plt.xlabel('a')
plt.ylabel('E')
plt.show()
ちなみに、最急降下法については、多くの場合、数学的に無限に解に辿り着かない、という特徴があります。
a の更新料が、傾きに応じて、どんどん小さくなってしまう為です。
それは、以下のリンクのような、アキレスと亀の話に似ているかもしれません。
しかし、アキレスと亀の距離が、ほぼほぼ 0 に近ければ、もう追いついたと言っても良かろう、という風潮です。
そもそも、コンピューターが浮動小数点を用いているが故の計算誤差の話もあり、その辺りは寛容に考えて良いかと思います。
先程の更新についても、更新を繰り返していくと、73回目の更新にて、a の更新がされなくなります。
これは、a の更新料が微小になりすぎて、0 に丸められてしまう為に起こる現象です。
以下が、その確認をするためのプログラムとなります。
import numpy as np
import matplotlib.pyplot as plt
a = np.arange(-100, 101) + 20
E = (a**2) + (-40 * a) + 2000
a_tmp = -50
eta = 0.2
iter_num = 200
for iter_i in range(iter_num):
E_tmp = (a_tmp**2) + (-40 * a_tmp) + 2000
dE_da_tmp = (2 * a_tmp) - 40
a_before = a_tmp
a_tmp = a_tmp - (dE_da_tmp * eta)
print('%d回目の更新:a = %.60f' % ((iter_i+1), a_tmp))
ただし、極稀に、とある a の更新時に、接線の傾きが 0 にピッタリ収まることがあります。
以下が、そのパターンです。
是非試してみて下さい。
import numpy as np
import matplotlib.pyplot as plt
a = np.arange(-100, 101) + 20
E = (a**2) + (-40 * a) + 2000
a_tmp = -50
eta = 0.5
iter_num = 10
for iter_i in range(iter_num):
E_tmp = (a_tmp**2) + (-40 * a_tmp) + 2000
dE_da_tmp = (2 * a_tmp) - 40
a_before = a_tmp
a_tmp = a_tmp - (dE_da_tmp * eta)
print('%d回目の更新:a = %.60f' % ((iter_i+1), a_tmp))
2変数の最急降下法
さて、ここまでで、1変数の最急降下法を説明させてもらいました。
次に、2変数の最急降下法についてです。
2変数の最急降下法で解く問題は、例えば、以下となります。

一気に複雑な形になりますね。
こうなると、平方完成は難しくなります。
尚、以下の記事に、平方完成の実施方法が紹介されています。
平方完成をやってみると、以下の式に変換できます。
要するに、a と b の2変数について、順を追って、(…)² の形にしていく感じで、ちょっとコツがいる感じですね。
先に、a と b の両方が含まれる (…)² を作って、次に、a か b のどちらかのみが含まれる (…)² を作ります。

この式を導けたことにより、(a + 2b − 1)² と、(b + 1)² の両方が 0 である場合に、E が最小値 74 を取ることが分かります。
また、(a + 2b − 1)² と、(b + 1)² の両方が 0 であるのは、b = −5、かつ、a = 11 の時であることも分かります。
次に、微分をして、接線の傾きが 0 となる a と b を探してみましょう。
上記の E の式を、a と b について微分すると、以下のようになります。

それぞれの微分値が 0 になる a と b を見つけたいので、∂E/∂a と ∂E/∂b の式の後ろに = 0 を付けて、以下の連立方程式を立てます。

この連立方程式を加減法などで解けば、b = −5、かつ、a = 11 が求まります。
次に、最急降下法による解の探索を行います。
微分式は、上記の ∂E/∂a と ∂E/∂b の式を使います。
尚、変数 a と b と、それによって求められる値 E の関係性をグラフに示すと、以下のような3次元のグラフとなります。







3次元のグラフになりますので、ぐるぐる回して観察する必要がありますね。
そして、E の式を微分して求められる ∂E/∂a と ∂E/∂b の式は、この E の3次元曲面に接する面の傾きになります。

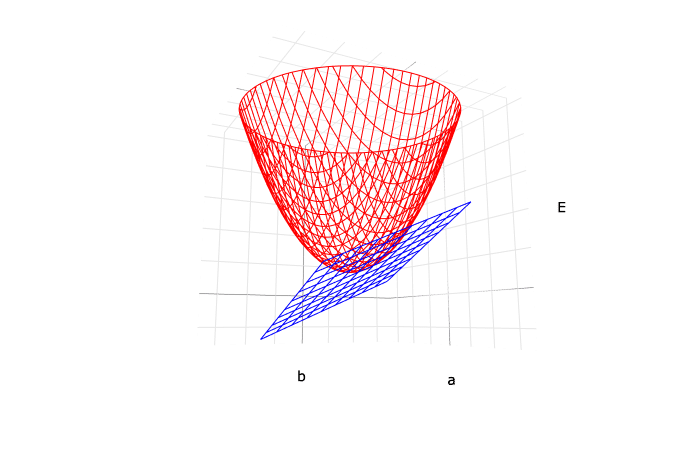




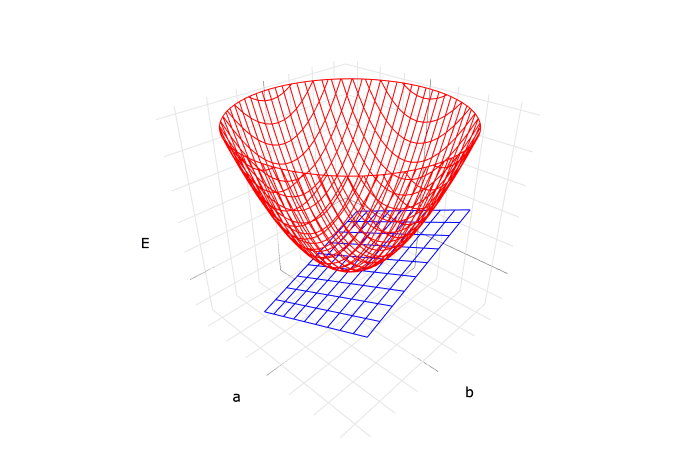
∂E/∂a と ∂E/∂b とで傾きが2つあること、或いは、接する対象が3次元の曲面であることから、接線ではなく接平面となります。
この記事が気に入ったらサポートをしてみませんか?

