チェビシェフの不等式をわかりやすく

前回のマルコフの不等式からの続きです。

マルコフの不等式は非負の確率変数に対するものでしたが、これを拡張したものがチェビシェフの不等式であり、非負の確率変数という制限が取り除かれています。

チェビシェフの不等式を導く

マルコフの不等式からスタートします。

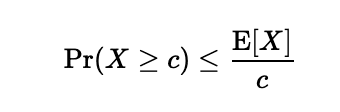
分母が大きくなれば推定する範囲がより狭くなりますが、これは線形的です。2次関数的に増加させることを考えて、すべてを2乗します。

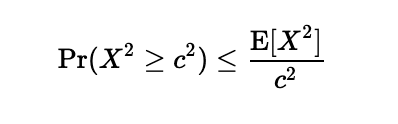
ここでX^2は"raw moments"と呼ばれる確率変数のみのモーメントです。一方で、"central moments"は平均からの距離を評価したモーメントです。

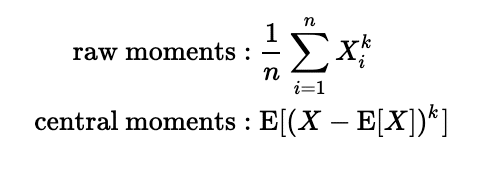
たとえば、1次のraw momentsは期待値、2次のcentral momentsは分散です。
raw momentsよりcentral momentsの方が望ましいので、XをX-E[X]とおくと

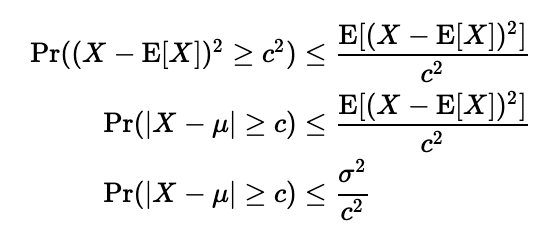
これがチェビシェフの不等式です。さらに、c=kσとおくと

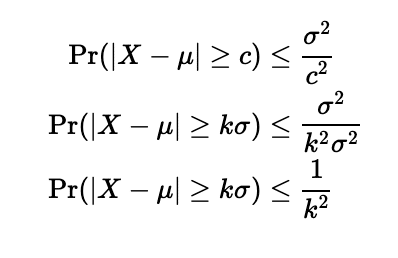
こちらの形だと、σ(標準偏差)が何個分という形で評価でき便利です。
この式が主張しているのは、たとえば、平均から2σを超えるデータが得られる確率は高々（多く見積もっても）1/(2^2)=25%ということです。分布の形状を問わず、期待値と分散がわかればその確率がわかります。

実際に使ってみる

Q.指数分布(λ=1)について、X≧aの確率をチェビシェフの不等式で考える。

この値は積分すればわかるのですが、チェビシェフの不等式を用いることで簡単におおよその範囲を導くことができます。

まず、期待値と分散を求めます。指数分布の期待値は1/λ、分散は1/(λ^2)です。

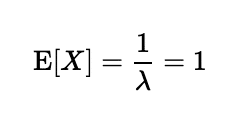
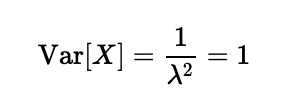
さて、X≧aの確率は以下のように書けます。

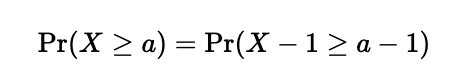
右辺のX-1に絶対値をつけると確率の範囲が広くなるので

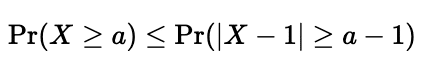
右辺にチェビシェフの不等式を適用すると

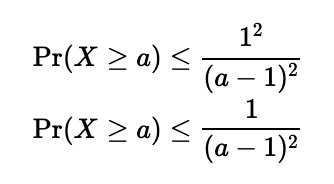
このチェビシェフの不等式が主張しているのは、X≧aの真の確率は1/(a-1)^2以下であるということです。では、真の確率はどうなるのか、実際に計算してみます。

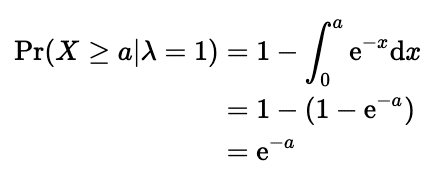
不等式が成立しているか、グラフで可視化してみます。

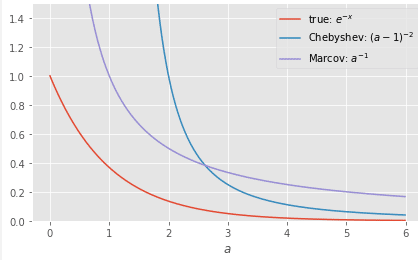
チェビシェフの不等式（青色）は真の値であるe^(-x)（赤色）より常に上側にあるので不等式が成立していることがわかります。くわえて、紫色はマルコフの不等式による境界を表しています（算出方法はこちら）。これによれば、aが約2.5以上になるとチェビシェフの不等式のほうが真の値に近いことがわかります。マルコフの不等式は期待値のみで確率を評価していましたが、チェビシェフの不等式は期待値と分散を用いることにより、（cが大きいという条件下で）より上界を狭めることが可能になることがわかります。

正規分布での例

次は標準正規分布の2σを例に挙げます。
標準正規分布において、2σを超える確率は下図の網掛けの面積であり、

4.5%です。こちらが真の値ですね。

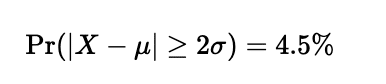
一方、チェビシェフの不等式から求めると、

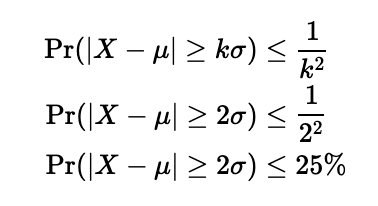
よって、チェビシェフの不等式が成立していることがわかります。

複雑な分布の場合

下図のような複雑な分布（混合分布）でもチェビシェフの不等式は適用できます。

実際に2σを超える確率を計算すると（この分布からデータをサンプリングして、2σを超えるデータの割合計算します）、2.4%でした。よって2.4%≦25%なので不等式が成立しています。

参考

新装改訂版現代数理統計学（竹村彰通）
現代数理統計学の基礎（久保川達也）
The Chebyshev Inequality, MIT OpenCourseWare
The Markov and Chebyshev Inequalities, Stanford Ben Lynn