地震計による河川流量の推定～長良川流域でやってみた～

1.防災科研の面白い研究成果

防災科研による興味深い研究成果を見つけた．
以下はそのプレスリリースと論文本体のリンク

高感度地震計で河川流量を推定する手法を開発～局地的な大雨で突発的に発生する河川洪水の予測が可能に～｜2021年度｜報道発表｜最新ニュース｜防災科研（NIED）

River discharge prediction for ungauged mountainous river basins during heavy rain events based on seismic noise data - Progress in Earth and Planetary Science

　RRIモデルにより計算した河川の流量波形と，その近隣の高感度地震計（約200m地中に設置）に記録された地震動の1-2Hzノイズパワーの波形がほぼ一致するようである（Fig.6）．

上記論文中のFig.6，両波形が非常に似た形状をしている

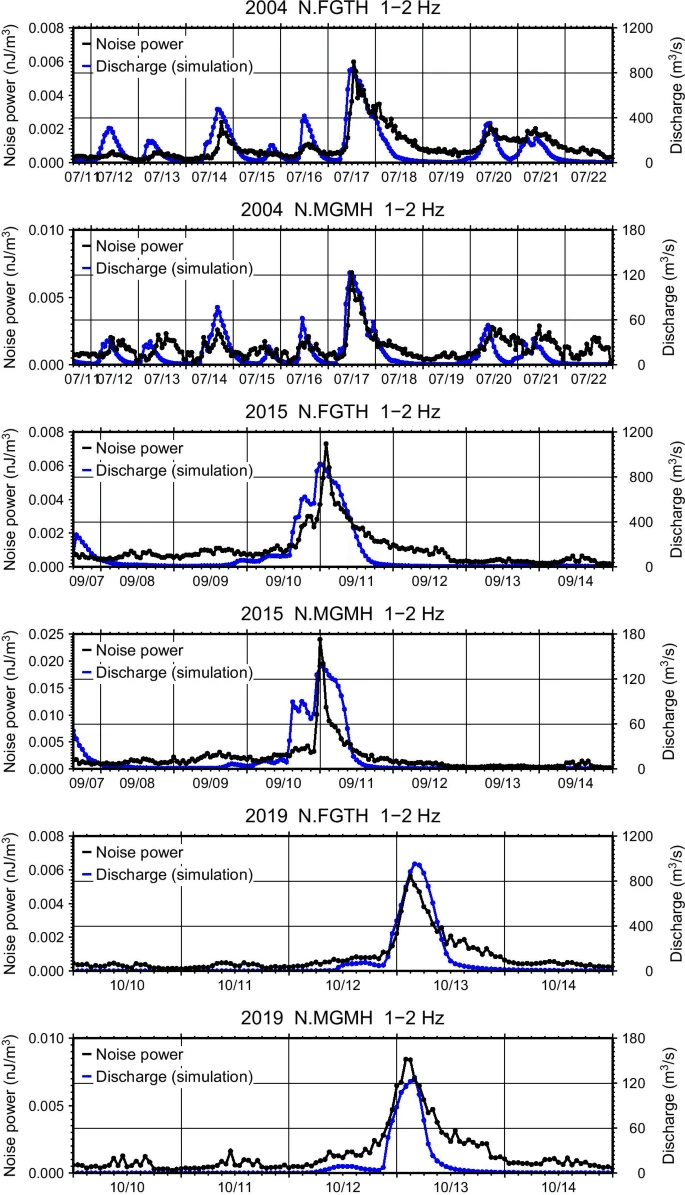
　本結果から，洪水時における河川の水流に起因した地震動が地表面から約200m地中まで伝わっていることが示唆される．衝撃的である．
　本研究成果は山形県の最上川流域を対象に行われたようである．そこで私は，岐阜県の長良川流域を対象に，本研究で用いられた手法をなるべく同じ条件で実施し，同じような結果が得られるか試してみた．

2.長良川流域への手法適用

2-1.対象地域と対象エリア

　対象地域は岐阜県長良川流域とする．本流域は上流域にダム等の流況操作施設が少なく，後述の流量計算がしやすいため対象地域として選ばれた．
　対象期間は同流域において直近で比較的大きな洪水が発生した，2020年7月6日~9日とする．なお対象期間内に長良川の計画基準点である忠節において，およそ10年に1度の流量に相当する4403$${(m^3/s)}$$が観測された．

2-2.地震動記録の取り扱い

　防災科研が運用する高感度地震観測網Hi-netは山間地を中心に全国約800地点で設置されており，長良川流域内には5地点で設置されている．これらの内，ここでは板取（観測点コード：N.ITDH），高鷲（N.TSUH），美並（N.MNMH）の記録を使用する．各地震計の位置を図-1に示す．

図-1　対象地域内の地震計と流量観測所の位置

　続いて各観測点の記録を，対象期間中の毎時前後10分間（56分-05分）の地震動記録を防災科研Hi-netのHP$${^{1)}}$$で取得する．（なおwindowsでは取得したデータを直接確認できないため，同HPで公開されているwin32ツールのうち，"dewin_32.exe"を使用してテキスト形式に変換する必要がある．）

　取得した毎時前後10分間の地震記録のうち，鉛直方向の記録値を物理値（次元はm/s）に変換した後，物理値に対して1分間ごとにFFTを実施する．毎時前後10分間のうち，1-2Hzの平均ノイズパワーが最小となる1分間をその時間の代表値として採用する．

2-3.河川流量データの計算

　分布型流出解析モデルであるRRIモデルにより地震計近傍の河川流量を推定する．RRIモデルへの入力条件として降雨データは気象庁の解析雨量，地形データは3sの解像度を持つMERIT Hydroを用いた．また計算結果の検証のため忠節，美濃，谷口の3地点で計算流量と観測流量を比較し精度を確認した．流量観測所を位置は図-1に示す．精度を示す指標としてNSE（式-1）とKGE（式-2）を用いた．
　なお流量観測所は上流域には設置されていないため，上流域での精度検証ができていない点に留意する必要がある．

$${NSE = 1-\dfrac {Σ_i (Q^i_{sim} -Q^i_{obs})^2}{Σ_i (Q^i_{obs} - \overline{Q}_{obs})^2}}$$（式-1）

$${KGE=1-\sqrt{(r-1)^2+(\frac{σ_{sim}}{σ_{obs}}-1)^2+(-\frac{\overline{Q}_{sim}}{\overline{Q}_{obs}}-1)^2}}$$（式-2）

ここで
$${Q_{sim}}$$：計算流量，$${{Q_{obs}}}$$：観測流量，$${\overline{Q}}$$：対象期間中の平均流量
r：計算流量と観測流量の相関係数，σ：計算流量と観測流量の標準偏差
を示す．

3.長良川流域での適用結果

3-1.RRIによる流量計算の結果

RRIによる計算流量の精度検証として，3つの地点における計算値と観測値の比較結果を図-2に示す．

図-2　3地点における流量計算結果の精度検証

　図-2より，ある程度の精度で流量を計算できていることがわかった．計算流量は観測流量と比べてやや小さく計算されているが，これ以上のパラメータ同定は面倒なので次に進む．

3-2.計算流量と地震計記録の比較

　板取，美並，高鷲における地震計の1-2Hzノイズパワーと，近傍河川の流量を比較した結果を図-3,4,5に示す．

図-3　板取における地震記録と河川流量の比較

図-4　美並における地震記録と河川流量の比較

図-5　高鷲における地震記録と河川流量の比較

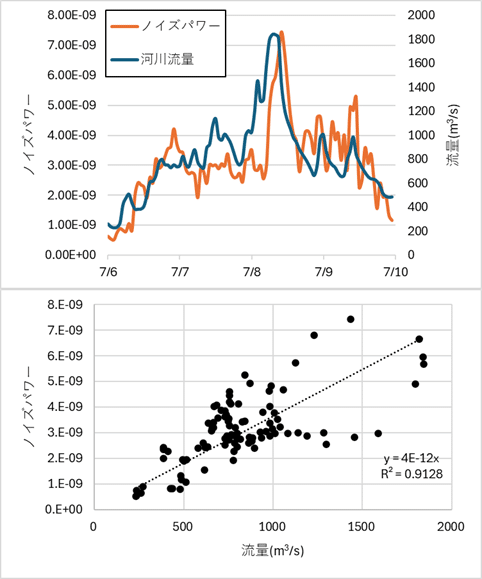
　図-3,4より，板取と美並では地震計ノイズパワーと近傍河川の流量の波形がほぼ一致した．両者を切片0の一次関数で近似したときの決定係数は0.9を超えており，地震計の記録から近傍河川の洪水流量を高精度に推定することができたようである．
　一方で高鷲では他の地点ほど両波形が一致しなかった（図-5）．高鷲は他の地点と比べ上流域に位置しており，計算流量の精度が低かった可能性が考えられる．

4.本手法の今後の展望に関する考察

　これまで流速の計測が困難であるために，山間部の流量は未知であった．それを地震計により推定する本手法は，やはり衝撃的である．

　今後流量の測定を目的とした地震計の設置が進むことを考えたが，その可能性は低いと考えられる．近年では非接触型の流速測定技術$${^{2)}}$$が向上しており，これを活用すれば山間地においても比較的簡易に流量を直接観測できるからである．地震計から流量を推定する本手法が重宝されるような場面は，私にはあまり思いつかない．

参考文献
1) 防災科研Hi-netのHP：http://www.hinet.bosai.go.jp/
2) 国土交通省 水管理・国土保全局：非接触型流速計測法の手引き
（案）https://www.mlit.go.jp/river/shishin_guideline/kasen/pdf/ryusoku_tebiki.pdf

あとがき①
本文中に記載した通り，高感度地震計は防災科学技術研究所が運用しており，本記事内で用いた地震計の記録は高感度地震観測網Hi-netのHP$${^{1)}}$$より取得した．

あとがき②
ノイズパワーの次元が分からない．Hi-netの地震計の物理値は速度(m/s)の次元を持っている．これをFFTした後に1-2Hzのノイズパワーを計算すると，2乗してから平均するため，$${(m^2/s^2)}$$という単位になるはずである．しかし論文には$${(nJ/m^3)}$$と記載されているのはなんで？