電験3種 2021年度 理論 問1 電気力線と電束

誘電体を挟んだ平行板コンデンサの内部における電気力線や電束の本数についての問題です。

（前提1）電気力線・電束とは？

電気力線・電束は，いずれも正の電荷を置いたときにどのように動くかを表した仮想の線です。上の図でプラスの電極の真ん中に赤い電荷を置くと，電荷はマイナスの電極に引っ張られて（プラスの電極に押されて）下に動きます。ほかの色の電荷でも同様です。端にある水色や紫色の電荷は点線のように膨らんだりしますが，問題文に「端効果は無視できる」と書いてあるので，他の電荷と同様まっすぐ動くと考えます（問題を解くうえでは細かいことを気にしなくていいということです）

（前提2）電気力線・電束の本数は？

電気力線も電束も，実際に存在するものではなく便宜上考えた仮想の線なので，本数も適当に決めればいいのですが，みんなで話をするときに便利なように次の通り決めました。

電気力線：電気力線の密度（単位面積当たりの本数）が，電界の大きさに等しい
電束：+Q [C] の電荷からQ [本] の電束が出て，-Q [C] の電荷にQ [本] の電束が入る

（前提3）平行板コンデンサの分割について

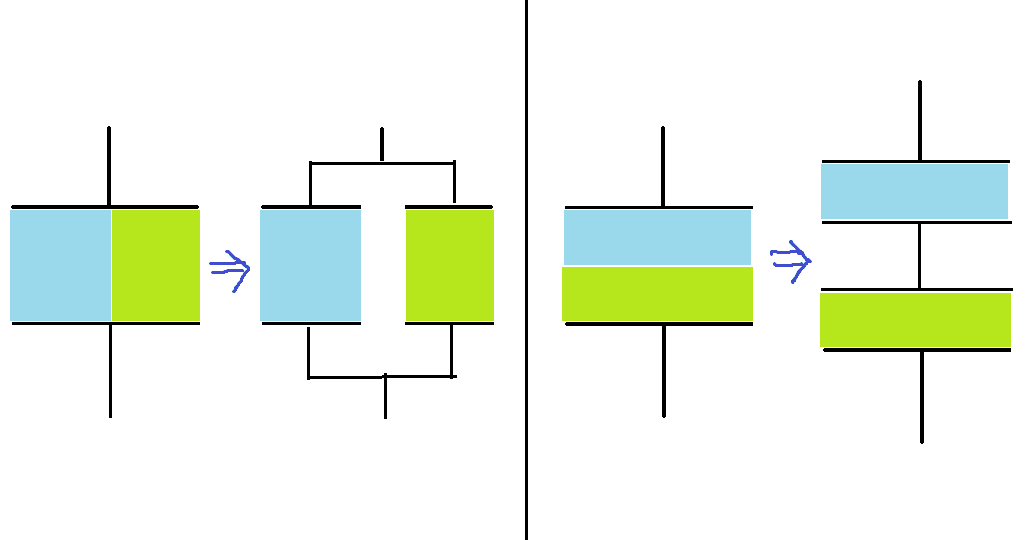
平行板コンデンサは上の図のように並列または直列のコンデンサに分けることができます。問題を解く上では，水色の部分と黄緑色の部分で誘電率が違うときによく使います。

（ア）電気力線の本数は？

「面S1と面S2の電気力線の本数の比を求めよ」という問題です。面S1と面S2の面積は等しいので「面S1と面S2の電気力線の密度の比を求めよ」と言ってもよくて，電気力線の本数の定義から「面S1と面S2の電界の大きさの比を求めよ」と言ってもいいわけです。

電界E [V/m] は単位長さあたりの電位の変化です（+1 [C] の電荷が受ける力 [N] という定義もありますが，今回は使いません）。平行板コンデンサにかかる電圧をV [V] ，極板間距離をd [m] として極板間の電界を考えると，マイナス側の極からd [m] 移動したときに電位がV [V] 上がるので，電界はV/d [V/m] となります（注：マイナス極からプラス極に行く間の電界が一定＝誘電率が途中で変わらない場合）

（前提3）を使ってS1側とS2側の2つのコンデンサに分けて電界を考えると，いずれもV/d [V/m] となり，等しいです。つまり（ア）に当てはまるのは1です。

（ウ）電束の総数は？

（イ）はちょっと飛ばして（ウ）を考えてみます。

「面S1と面S2の電束の合計を求めよ」という問題，すなわち「コンデンサ全体の電束を求めよ」ということになります。電束の本数＝電荷ですから「コンデンサ全体の電荷を求めよ」となるので（ウ）はQです。

（ア）1，（ウ）Qということで，選択肢から解答は1に決まります。

（イ）それぞれの電束は？

解答は求まりましたが，念のため（イ）も計算しておきましょう。「面S1と面S2の電束の本数の比を求めよ」という問題ですが，S1とS2の面積が等しいので「面S1と面S2の電束の密度の比を求めよ」としてもいいし，電束の本数＝電荷なので（前提3）を使ってコンデンサを2つに分けて「S1側とS2側のコンデンサの電荷の比を求めよ」としてもいいです。

（イ解法1）電束密度と電界の関係式で解く

実は電束の密度と電界（＝電気力線の密度）には
D＝εE（D：電束密度，ε：誘電率＝ε0×εr，E：電界＝電気力線の密度）
という関係があります。

これを利用して，
S1の電束密度をD1，S2の電束密度をD2とすると，電界Eは等しいことから
D1＝ε0×ε1×E，D2＝ε0×ε2×Eより
D1/D2＝ε1/ε2と求められます。

（イ解法2）コンデンサの電荷で考える

D＝εEの式を覚えてなくても大丈夫です。S1側とS2側のコンデンサに分けてそれぞれの電荷を考えます。2つのコンデンサは比誘電率以外の条件が同じです。比誘電率が高いほど優秀なコンデンサになり，同じ電圧でたくさんの電荷がためられるようになります。比誘電率ε1がε2の2倍と仮定すると，たまる電荷Q1はQ2の2倍になり，面S1の電束は面S2の電束の2倍，これを満たす選択肢はε1/ε2という具合です（まじめな計算は蛇足2で）

（蛇足1）コンデンサ外部の電気力線・電束

（前提1）で電気力線・電束をコンデンサ内部にだけ書きました。コンデンサ外部はどうなのか気になるかもしれません。試しに外部にも正の電荷を置いてみたのが下の図です。

コンデンサ内部に置いた電荷にはプラス極からもマイナス極からも図の下向きに力が加わります。なので電荷は下向きに動きます。一方，コンデンサ外部に置いた電荷には各極から逆向きの力が加わります。（端効果が無視できる＝極板が無限に大きいとき）各極の電荷の大きさが等しければ力の大きさも等しいので，電荷は動きません。つまり，コンデンサ外部に電気力線・電束はありません。

（蛇足2）コンデンサの電荷を求める

（イ解法2）をまじめに計算してみましょう。コンデンサにたまる電荷は，
Q＝ C× V（Q：各極板にたまる電荷 [C] ，C：コンデンサの静電容量 [F]，極板間の電圧 [V] ）
で表せます。静電容量Cはコンデンサの性能を表す数字です。静電容量Cが大きいほど同じ電圧Vでもたくさんの電荷Qをためられる優秀なコンデンサということです。

じゃあ静電容量Cはどうやって求めるのかというとこんな式で表されます。
C＝ε0×εr×S/d（ε0：真空の誘電率 [F/m]，εr：比誘電率，S：各極板の面積 [m^2]，d：極板間の距離 [m]）
真空の誘電率ε0（イプシロンゼロ）は約8.85×10^-12という定数ですが，特に覚える必要はありません。比誘電率εrは極板の間に入れる誘電体が真空より何倍すごいかをあらわす数字です。例えば紙の比誘電率εr＝3ぐらいなので，紙を入れると静電容量Cが3倍になって3倍すごいコンデンサになります。また，極板の面積Sが大きいほど，極板間の距離dが小さいほどいいコンデンサになります。

いま求めたいのは，「面S1の電束は面S2の電束の何倍か」なので，電束の本数＝コンデンサの電荷という定義から「S1側のコンデンサの電荷はS2側のコンデンサの電荷の何倍か」という問題になります。

電荷の式 Q＝C×V の C に，静電容量の式 C＝ε0×εr×S/d を代入すると，
Q＝ε0×εr×S/d×V
なので，S1側のコンデンサの電荷をQ1，S2側のコンデンサの電荷をQ2，面S1の面積（＝面S2の面積）をS，極板間の距離をdとすると，
Q1＝ε0×ε1×S/d×V
Q2＝ε0×ε2×S/d×V
となり，求めるQ1/Q2＝ε1/ε2となります。