点と直線の距離の2つの証明方法
点$${(x_1,y_1)}$$と直線$${ax+by+c=0}$$の距離は $${d=\dfrac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}}$$
証明1(直線の方程式の利用)

まず、原点$${\textrm{O}}$$と次の直線の距離$${d}$$を求めてみる。
$${ax+by+c=0 \cdots①}$$
$${\textrm{O}}$$を通り直線①に垂直な直線は
$${bx-ay=0 \cdots②}$$
で表される。2直線①、②の交点を$${\textrm{H}(p,q)}$$とする
$${p=-\dfrac{ac}{a^2+b^2}}$$、$${q=-\dfrac{bc}{a^2+b^2}}$$
$${d=\textrm{OH}}$$であるから、
$${d=\sqrt{p^2+q^2}=\sqrt{\dfrac{c^2(a^2+b^2)}{(a^2+b^2)^2}}}$$
$${=\dfrac{\sqrt{c^2}}{\sqrt{a^2+b^2}}=\dfrac{|c|}{\sqrt{a^2+b^2}}}$$

次に、点$${\textrm{P}(x_1,y_1)}$$と直線$${ax+by+c=0}$$の距離$${d}$$を求めてみる。直線$${ax+by+c=0}$$を$${l}$$とする。点$${\textrm{P}}$$と直線$${l}$$の両方を、$${\textrm{P}}$$が原点$${\textrm{O}}$$に重なるように平行移動し、移動後の直線を$${l^{\prime}}$$とする。
$${l^{\prime}}$$上のどんな点$${(x,y)}$$に対しても、点$${(x+x_1,y+y_1}$$が$${l}$$上にあることから
$${a(x+x_1)+b(y+y_1)+c=0}$$
が成り立つ。すなわち
$${ax+by+(ax_1+by_1+c)=0}$$
これが$${l^{\prime}}$$の方程式である。原点$${\textrm{O}}$$と直線$${l^{\prime}}$$の距離は $${\dfrac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}}$$ で、これが求める$${d}$$に等しいので、
$${d=\dfrac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}}$$
証明2(法線ベクトルの利用)
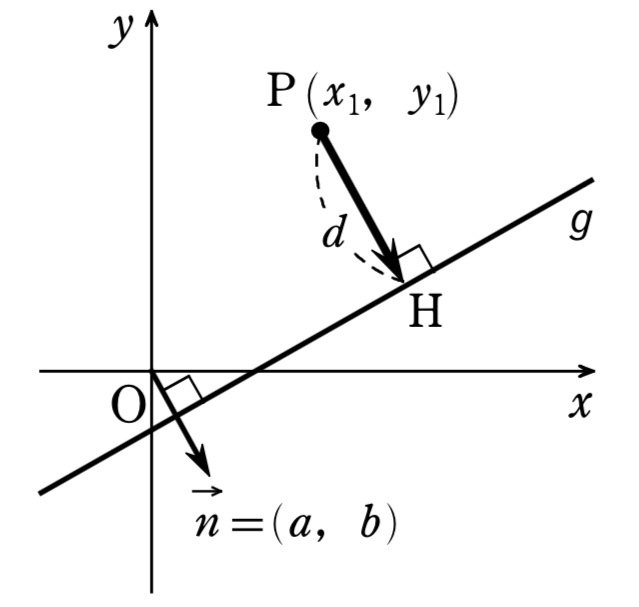
直線$${ax+by+c=0}$$を$${g}$$とする。点Pから直線$${g}$$に垂線$${\textrm{PH}}$$を下ろすと
$${d=|\overrightarrow{\textrm{PH}}|}$$
$${\overrightarrow{n}=(a,b)}$$は直線$${g}$$の法線ベクトルで、$${\textrm{PH}}$$は$${\overrightarrow{n}}$$に平行であるから
$${\textrm{PH}=t\overrightarrow{n}=t(a,b)}$$
となる実数$${t}$$がある。$${\overrightarrow{\textrm{OH}}=\overrightarrow{\textrm{OP}}+\overrightarrow{\textrm{PH}}}$$から、$${\textrm{H}}$$の座標
$${(x_1+ta,y_1+tb)}$$
と表される。点$${\textrm{H}}$$は直線$${g}$$上の点であるから
$${a(x_1+ta)+b(y_1+tb)+c=0}$$
すなわち $${t(a^2+b^2)+(ax_1+by_1+c)=0}$$
よって $${t=-\dfrac{ax_1+by_1+c}{a^2+b^2}}$$
したがって $${d=|\overrightarrow{\textrm{PH}}|=|t||\overrightarrow{n}|}$$
$${=\dfrac{|ax_1+by_1+c|}{a^2+b^2} \times \sqrt{a^2+b^2}}$$$${=\dfrac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}}$$
この記事が気に入ったらサポートをしてみませんか?
