ABC191の解答

AtCoder Beginner Contest 191を解き終わりましたのでその解答を書いていきます。問題はこちらから。

AtCoder Beginner Contest 191 - AtCoder

難易度は以下の通りでした、

A 25（灰）
B 20（灰）
C 1063（緑）
D 1953（青）
E 1323（水）
F 2333（黄）

C、Dが難しかったですね。先頭の問題から解いてしまうと大変だったかもしれません。よくできたあなたも、まだまだだったあなたもしっかりと復習していきましょう。ではいきます。

A Vanishing Pitch

速さ v [m/s]の等速で飛んでくるボールが投げた後、t [s]から s [s]まで消えています。バッターは d [m]離れています。ボールが消えている間は打つことができません。さて、ボールを打ち返せますことはできますか。

という問題です。

落ち着いて考えればそんなに難しくありません。まず、速さと時間から距離求めましょう。「みはじ」というのか「はじき」というのかわかりませんが、

距離＝速さ×時間

で求まります。そしてこの距離を使えば、以下の図で一発です。

この打てないゾーンにバッターがいたら打てません。ですので、

vt <= d <= vs

が打てない条件となります。境界条件のときも打てません。そこには注意！

あとは実装するだけです。

#include<bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define reps(i,s,n) for(int i=s;i<n;++i)
using namespace std;
using ll = long long;
using P = pair<int, int>;

int main()
{
   int v, t, s, d;
   cin >> v >> t >> s >> d;
   if (v * t <= d && d <= v * s) cout << "No" << endl;
   else cout << "Yes" << endl;

   return 0;
}

私のわがままですが、t と s が逆の方がわかりやすかったなーって思います。なんで、消え始めが t なんだろう、、時間だからかな？

B Remove It

長さ n の整数列 A から x を取り除いて、残った要素を全部出力する。

という問題です。これは指示通りに A から何らかの操作で x を消した配列 A' を生成してももちろん解けます。が、少し面倒です。

ですので、入ってきたものをそのまま出力する。でも、関門を設けて x だけは通さないようにする。としてあげましょう。さながら、空港の機内持ち込み検査のような感じです。 x は金属探知機で反応してしまいます。

ということで実装しましょう。

#include<bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define reps(i,s,n) for(int i=s;i<n;++i)
using namespace std;
using ll = long long;
using P = pair<int, int>;

int main()
{
   int n, x;
   cin >> n >> x;
   rep(i, n)
   {
       int a; cin >> a;
       if (a == x) continue;
       else cout << a << " ";
   }
   cout << endl;

   return 0;
}

出力は改行指定でないのでそこに注意しましょう。あとはなんでしょう、、今回は時間に余裕がありますので問題にならないのですが、複数回出力を出す問題ではcoutがネックになる可能性があります。この処理はちょっと重いです。クエリ処理の問題とかで「あとちょっと間に合わない」ってときはprintfを使うと幸せになれるかもしれませんね。

C Digital Graffiti

マス目が黒か白かで塗られます。黒で塗られたマスが表す図形が何角形なのかを判定しましょう。

という問題です。この問題は結構悩みました。サンプルでは四角形の例が出ているのですが、では以下の図はどうでしょう、という問題に出くわしました。

いわゆるテトリスのTミノってやつです。この図形は何角形なのでしょうか？三角形？八角形？

と少し悩みます。しかし、正直なところ三角形にはだいぶ主観が入っています。こうであったら面白いなという、、落ち着いて考えれば、誰が見ても一意に定まる八角形と考えるのが自然でしょう。私も三角形と考えたので気持ちはわかりますが問題文にこちらから歩み寄りましょう。

さて、右図が八角形となるのはわかりました。ようやく問題の本質に入ります。角がいくつできるかです。

角ができるかですので、角の気持ちになって、角ができうる場所を探っていきましょう。右のTミノについて角に注目した図を示します。

点の集合体が苦手な人はすみません。私もすこしそわそわします。

この図で角になりうる点は緑とピンクの丸で示した12か所となります。そしてそのうち8か所が実際に角となっており、その結果8角形という答えになるわけです。

ここで大切なのは、

角ができるかどうかはその周囲4マスにしか依存しない

ということです。これに気づくことができるとグッと正解に近づけると思います。4マスに絞れるならその状態は16通りしかありません。16通りぐらいなら全部見てあげても良いのではないでしょうか。私は今から見ていきます。どうぞお付き合いください。

〇は角になって、×はなりません。また、ななめに黒が出現するパターンは問題文の条件から存在しません。たぶん。

上の図を見るとどうやら黒の数が奇数のときに〇、偶数のときに×となっているようですね。

ということで、上記の「角になりうる点（緑とピンクの点）」に関して偶奇の判断をしてあげましょう。奇数となった点の数が求める出力となります。

いろいろと考えましたが、やることは結構シンプルですね。実装しましょう。

#include<bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define reps(i,s,n) for(int i=s;i<n;++i)
using namespace std;
using ll = long long;
using P = pair<int, int>;

int main()
{
   int h, w;
   cin >> h >> w;
   vector<string> s(h);
   rep(i, h) cin >> s[i];

   int ans = 0;
   rep(i, h-1)rep(j, w-1)
   {
       int ti = i;
       int tj = j;
       int cnt = 0;
       rep(tti, 2)rep(ttj, 2)
       {
           if (s[ti + tti][tj + ttj] == '#') ++cnt;
       }
       if (cnt & 1) ++ans;
   }
   cout << ans << endl;
   return 0;
}

角の視点で回してるので配列の添え字には気を付けましょう。 h-1と w-1で回すことになります。

D Circle Lattice Points

円の内部（境界も含む）にある格子点を数え上げます。ただし、入力は最大？最小？少数第四桁まで与えられるので、そこに注意してね。

という問題です。

非常に苦労しました。そのため、本解説記事もどのように書こうかとても迷いました。迷った結果、まず厳密な議論を抜きにして大体どんな感じのアプローチで数え上げを行うか一通り説明したのちに、小数や内部判定など細かな説明を付け加えていこうと思います。

ではいきます。

こんな感じの円を考えていきます。

特に座標の指定もしてません。適当です。ただし、点線はx,yが整数のところに引かれています。

このくらい小さければ自力でも数え上げができますね。１７個かな。でもこれが大きくなると数えるのはしんどいです。そのため、いい感じで数える方法を考えます。

今回は

各 y 座標（横の破線）において円の中心（黒点）より右と左に何個点があるか

で数えます。例えば、一番上の破線は左右ともに0個、その1個下は左に1個右に2個、といった感じです。

次にその点を効率よく数え上げていきます。簡単のために（書くのが大変なので）右側だけ説明をしますが、左側も同様です。

数え上げには隣り合う2つの点を用いて、その2点が内側か外側かで判定をしていきます。2点のうち中心に近いほうをp1, 遠いほうをp2(=p1+1)とします。この点を右に左に動かしていくことにより格子点を数えていきます。

先に結論を述べますが、この点の関係って次の4通りしか存在しません。

格子点の数が決定（p1もしくは0）したら次の軸に移動します。このとき、現在のp1の値は覚えておきましょう。次の軸のp1って前の軸のp1の近くにあるはずです。そのため、毎回中心近くから計算するよりもはるかに高速に格子点を求めることができます。最後にざっくりですが、格子点を求める流れを図示します。

さて、ここまで厳密な議論を避けて格子点の求め方を説明しました。ということでここからは、少々複雑ですが小数の対処などを説明していきます。

まずは、今後の議論をしやすくするために円を第一象限に限定しましょう。幸いなことに、グリッドは無限遠まで広がっていますので、対称性が存分に使えます。入力として与えられる中心のx,y座標を平行移動しても良いのですが、今回はx軸とy軸それぞれに関して対称移動しましょう。

if(x < 0) x*=-1;
if(y < 0) y*=-1;

これで大丈夫です。これをすると、中心の右側、左側が考えやすくなります。

続きまして内側に入っているかの判定方法です。これは円というものは中心から等距離にある点が作る図形で、その方程式は

(x-a)^2+(y-b)^2 = r^2

だから

(x-a)^2+(y-b)^2 <= r^2

で終わりなのですが、さすがに不親切なのでもうちょっと書きます。要は円の中心から、考えたい点（上記の説明でいくとp1,p2）までの距離と半径を比較すればよいわけです。点が半径よりも遠ければ外側ですし、以下であれば内側です。コタツに入って、一歩も動かずにとれる範囲にものがあるかどうか、という感じですかね。このときの手の長さが半径 r です。

3平方の定理よりこの斜辺の長さが求まりますね。この長さが r 以下であれば内側です。ただし、このままだとルートが出てきてしまいますので、両辺2乗しましょう。そうすると、

(x-a)^2+(y-b)^2 <= r^2

となり、先ほどと同じ式が得られました。

さて最後に少数に関する議論です。ここがややこしいです。そのまま計算すると誤差が生じて答えが求まりません。問題文には「高々少数第4位まで与えられる」とあります。単純に考えて10000倍をしてあげれば小数部分は消えます。ということで、10000倍すれば答えが求まるんだから、その結果を最後に10000で割ればいいんじゃないか、と考えますがそんなに甘くはありません。

というのも、いままで格子点となっていた 「x, yともに整数の座標」というものを変化してしまうからです。10000倍することで10000倍伸びてしまいました。この座標平面上では値が1増えても、元の座標でいうと0.0001しか増えません。これでは、格子点とは言えませんね。でも、逆に言えば変わったことはそれだけです。元の世界で1増やしたければ、変換後の世界で10000増やせばよいです。つまり、変換後の世界では「10000の倍数のx, y」が格子点となるのです。

では、いままでは厳密な座標を用いずに説明してきましたが、重い腰を上げてしっかりと表現する方法を考えましょう。

今まで考えてた図に元の世界の座標を与えてみましょう。中心(3.8242, 5.2451)とでも置きます。このとき、探索開始時の右側の中心に近い点p1および左側の中心に近い点q1は次のように表されます。

p1 = 3 + 1 = 4
q1 = 3 - 0 = 3

この「3」は中心のx座標の整数部ですね。また、右と左で開始地点が異なっています（p1は格子点の数と表現できますが、q1は格子点の数-1個に対応します。また、先ほど第一象限に限定しているため入れ替わることはありません）。

では、この関係を変換後の世界に飛ばしてみましょう。

p1 = 30000 + 1 * 10000 = 40000
q1 = 30000 + 0 * 10000 = 30000

こんな感じです。先ほどより数はだいぶ大きくなりましたが、本質は変わりません。このときのp1が右側格子点の数、q1+1が左側格子点の数に対応します。また、y 座標も10000の倍数となることに注意しましょう。

実装時の注意として、10000倍する際に*10000とすると、丸め誤差が生じます。そのため、c++ではround()という関数を用いています。

長くなりましたが実装です。

#include<bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define reps(i,s,n) for(int i=s;i<n;++i)
using namespace std;
using ll = long long;
using P = pair<int, int>;

const int b = 10000;

ll x, y, r;
ll xd; //10000以下を切り捨てたｘ

bool judge(ll xi, ll yi)
{
   ll dist = (xi - x) * (xi - x) + (yi - y) * (yi - y);
   return dist <= r * r;
}


ll f(ll s, ll t)
{
   ll res = 0;
   ll left = 0;
   ll right = 1; //計算の都合上rightは1を基準にする

   for (ll i = s; i >= t; i -= b)
   {
       //左側を数え上げる
       while (1) 
       {
           bool ok1 = judge(xd -left * b, i);
           bool ok2 = judge(xd -(left+1) * b, i);
           if (ok1 && ok2) ++left;
           else if (ok1 && !ok2)
           {
               res += left + 1; //leftは+1したものを答え加える
               break;
           }
           else
           {
               if (left == 0) break;
               else --left;
           }
       }
       //右側を数え上げる
       while (1)
       {
           bool ok1 = judge(xd + right * b, i);
           bool ok2 = judge(xd + (right + 1) * b, i);
           if (ok1 && ok2) ++right;
           else if (ok1 && !ok2)
           {
               res += right; //rightはそのまま答えに加える
               break;
           }
           else
           {
               if (right == 1) break;
               else --right;
           }
       }
   }
   return res;
}

int main()
{
   double tx, ty, tr;
   cin >> tx >> ty >> tr;
   x = round(tx * b);
   y = round(ty * b);
   r = round(tr * b);
   //第一象限に持ってくる
   if (x < 0) x *= -1;
   if (y < 0) y *= -1;
   //xの下4桁を捨てる
   xd = x / b;
   xd *= b;
   //最大ケースにおける端点のy座標の絶対値におまけをつける
   ll inf = 2e9;
   ll ans = f(inf+50000,-inf-50000);
   cout << ans << endl;
   return 0;
}

この問題は苦戦しました。考察してるとき、実装してるとき、解説記事をかいてるとき、すべてにおいて頭が混乱してました。小数点の扱いはややこしくて難しいですね。でも、なんとか言語化できたのではないでしょうか。少々長くなりましたが、、、

E Come Back Quickly

n 個の街と m 本の一方通行の道があります。道にはコストが設定されています。ある街から出発して1本以上の道を通ったのちに元の街に帰ることができるか判定します。また、帰れる場合には最短経路（最小コスト）を出力してください。

という問題です。

最短経路問題です。ということで、ダイクストラ法やらワーシャルフロイト法など何かしらを使いましょう。今回はダイクストラ法を用いました。

さて、まずは

元の場所に戻ってくる

という操作をダイクストラ法に落とし込みましょう。今回、ダイクストラ法の詳細な説明はしません。ということで、とりあえずは

任意の点から他の点までの最短距離を求める

魔法のアルゴリズムということにしておきます。

また、少し拡張することで「初期点は複数」とすることが可能となります。それは後程。

次のグラフの状態を考えていきます。

辺の数字は移動コストです。

まずは街1から出発する場合を考えましょう。ダイクストラ法では初期状態として出発点の距離を0として、ほかの街までの距離をinfとします。なんやかんや計算をしていき、infよりも近い道が見つかればどんどん更新をしていきます。今回は1から出発するので、1までの距離を0、他の街までの距離をinfとして探索を始めます。

というのが普通のダイクストラ法です。

でも今回は、「戻れるかどうか」の判定です。街1から始めてしまったら、戻れるかどうかよくわからなくなります。そのため、街1から1つ分進んだ街である３を初期点としてみましょう。そのため、街3以外の距離をinfにして、街3の距離を通ってきた道のコストである1とします。ここから探索開始です。少しややこしいのですが、ダイクストラ法の初期状態は街3からのスタートとなるのですが、求めたいのは街1からの距離ですのでこんな感じになります。

言い換えるのであれば

街3から街1までの距離＋街1から街3までの道の距離

が求める答えです。おそらく今回は１→３→５→１のコスト８が最小となるでしょう。

続きまして２から出発する場合です。先ほどと同様に２から一つ進んだ街である３を初期点としましょう。ただ今回は先ほどとは通った道が違うので３までの距離は３としてスタートです。探索をした結果、街２までの距離はinfになっていると思います。それもそのはずで、街２に行くための道はありません。街２を出発したら戻れないのです。距離の更新ができませんね。

ということで、距離がinfのままでしたら戻れないということで、-1を出力しましょう。

最後に3から出発する場合を考えましょう。3からは複数の街に行くことができます。ここからが、ダイクストラ法を複数の点から探索する方法になります。といいましても、同様の操作を複数回行うだけです。初期点として、街４（コスト5）、街5（コスト２）、そして自己ループの街３（コスト500）の3つを初期点とします。もしも、同じ街に行く道が複数ありましたらコストの小さいほうを距離としましょう。ここ大事です。入力例3に引っかかります。今回は自己ループがあるので道1つで戻ることは可能ですが、別の道を通ったほうがコストは小さそうですね。３→５→１→３のコスト8が最小です。

初期状態の比較図を載せておきます。

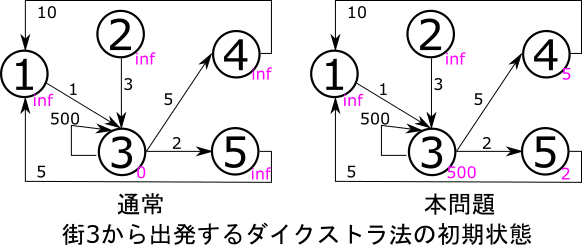
以上の操作を全部の街を始点にして行いましょう。

さて、実装です。

#include<bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define reps(i,s,n) for(int i=s;i<n;++i)
using namespace std;
using ll = long long;
using P = pair<int, int>;

int main()
{
   int n, m;
   cin >> n >> m;
   vector<vector<P>> edge(n);
   rep(i, m)
   {
       int ai, bi, ci;
       cin >> ai >> bi >> ci;
       --ai; --bi;
       edge[ai].emplace_back(bi,ci);
   }
   const int inf = 1e9;

   rep(i, n) {
       vector<int> d(n, inf);
       priority_queue<P, vector<P>, greater<P>> pq;
       //次の街を初期点として書き込む
       for (auto a : edge[i])
       {
           int bi, ci;
           tie(bi, ci) = a;
           d[bi] = min(d[bi],ci);
           pq.emplace(d[bi], bi);
       }

       while (!pq.empty())
       {
           ll c = pq.top().first;
           int s = pq.top().second;
           pq.pop();
           if (d[s] < c) continue;
           for (auto a : edge[s])
           {
               int gt = a.first;
               int gc = a.second;
               if (d[gt] <= d[s] + gc) continue;
               d[gt] = d[s] + gc;
               pq.emplace(d[gt], gt);
           }
       }
       if (d[i] == inf) cout << -1 << endl;
       else cout << d[i] << endl;
   }
   return 0;
}

ダイクストラ部分を関数化するなりすればもうちょっと綺麗に書けますね。

ダイクストラの記事を書きたいのですが、私はアルゴリズム解説記事を書くと宣言してなかなか書かないプロですので気長にお待ちいただければと思います。

あと、お恥ずかしながら経路探索の計算量の理解が浅く厳密な議論ができません。ベルマンフォード法がafter contestで落ちるようになったそうですが、ほかの手法はどうなのでしょうか。

F GCD or MIN

n 個の数字があります。この数字のうち2つ選択してminかgcdをとります。これを数字が1つになるまで行った時に、残る数字の候補はいくつありますか。

という問題です。

このままだと考えにくいので、まずは問題文の読み替えをしたいと思います。

まず、残る数字の条件を考えていきます。 x, y (x <= y) で　min(x,y) およびgcd(x, y)の演算結果はともに x 以下になります（minは当然そうですね。gcd　も少し考えてみると、x, yの共通の約数→ x より大きくならない、となります）。これをすべての数字について行うため、条件として「n個の数字の最小値以下」というものが浮かんできます。

次にgcdをうまく使うことを考えます。n 個の数字から1つ以上選択してそれらの gcd を取ることでいろいろな数が表現できます。そして、選択されなかった数はその結果に対してminを取ることで邪魔することなく取り除くことが可能です。とは言いましたが、ここで上の条件が効いてきます。表現した数（d とします）が、n この数字の最小値(m とします)以下であれば、問題ありません。使わなかった数字は m 以上であることが保証されますので、min演算により d が残って、使われなかった数が消えます。しかし、d > mだとさあ大変。min 演算で d が消えてしまいます。この場合の d は本問題では表現できないのです。（min をとってから gcd としても、 gcd をとってから min をしても、いくつか数字を選択しそのgcdを取ってminをすることと変わりません）。

どうやら、いい感じに数を選択したときのgcdが m 以下であればその数は残りそうですね。

ということで問題は次のように読み替えることができます。

n個の数字の最小値を m とする。
n 個の数字の部分集合のgcdのうち m 以下の個数はいくつですか。

この問題を考えます。

まず、最小値を m を求めます。これは簡単ですね。minでもifでもよいので、さくっと求めましょう。

次に n 個の数字の部分集合のgcdを求めます。ここが本問題の本質です。愚直解法では、部分集合を全列挙する必要があります。各数字に関して集合に入れる、入れないの2通りありますので、部分集合は 2^n 通りあります（空集合を除くと2^n-1）。制約を見ると n<= 2000ですので、2^2000ですね。これは厳しそう。

ということでなんらか工夫がいるわけです。ここで、部分集合のgcdになりうる値について考えます。厳密にいうのであれば、部分集合のgcdになるための必要条件です。もし、この条件に当てはまっていたら、部分集合のgcdになれる”かも”ね。でも、当てはまらなければ絶対なれないよ。ってやつです。

gcdと書いてきましたが、こいつは「最大公約数」です。2つ（または複数）の数字の約数で、共通している約数のうち、その最大の数字です。つまり候補は元の数字の約数に絞られるわけです。

例えば、6と9でしたら、その最大公約数の候補は6の約数｛1,2,3,6｝と9の約数{1,3,9}の和集合{1,2,3,6,9}に限定されます（このとき公約数は積集合{1,3}で最大公約数は3となります）。つまり、4,5,7,8に関してはそもそも考える必要がないということです。

ということで、計算の流れは次のようになります。

n 個の数字の全ての約数を列挙する。
この約数が部分集合のgcdの候補となる。
↓
実際にこの候補が部分集合の約数になっているか判定する。

約数列挙は数字aに対して、 a % i == 0 の判定をして、trueなら i は約数。また、a / i も同様に約数である。という方法を用いれば、√aの計算量で求めることが可能です。これにより候補を求めることができました。

次にこれらの候補が実際に部分集合の約数になっているか判定していきます。これは

ある数 d を約数に持つ数の最大公約数が d となる

という方法で判定可能です。d を約数に持つ数だけの部分集合を構成してそのgcdを計算するということです。もし、d を持たないものを部分集合に入れた場合には d がgcdとなることはありません。３が部分集合の約数になるかなーって考えているときに、{6,8,9}という部分集合では8が邪魔をしてしまいます。この 8 はmin演算の方に流しましょう。8 より小さい数字のgcdの結果とのminですので、8 は邪魔することなく消えてくれます。

また、d の約数だけで部分集合を構成したのに、最大公約数が d にならないパターンも見てみましょう。d=3、部分集合{12, 18, 36}とします。どれも3を約数に持ちますが、gcd(12,18,36)=6ですね。dよりも大きな値が出てきました。残念ながら3は部分集合の約数にはなれません。一方で、dを約数に持つ数字の集合なので、その集合のgcdがd 未満になることはありません。

判定は上記の方法で行います。次にこれを効率よく行う方法を説明します。

私はc++を用いてますので、連想配列（map,unordered_map）を用います。アルゴリズムは次の通りです。

１．ai を受け取り、約数列挙する。
２.  約数に関して ai その約数 dij を持つ数字とのその時点でのgcdを保持する。（map[dij] ← gcd(map[dij], ai)）
３．すべての ai について行った後、map[d] = d となったものが部分集合の約数

ここで、map[d]を用いていますが、これは約数 d を持つ数字の最大公約数を記録しています。最大公約数の演算結果はその計算順序により変化しないので、どんな順番で数が入力されても大丈夫です。

あとは、部分集合の約数となった数字のうち最小値 m 以下の数字の個数を数えてあげればそれが答えになります。 

実装です。

#include<bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define reps(i,s,n) for(int i=s;i<n;++i)
using namespace std;
using ll = long long;
using P = pair<int, int>;


int main()
{
   int n;
   cin >> n;
   unordered_map<int,int> mp;
   int mn = 1e9 + 5;
   rep(i, n)
   {
       int a;
       cin >> a;
       mn = min(mn, a);
       vector<int> d;
       for (ll i = 1; i * i <= a; ++i)
       {
           if (a % i != 0) continue;
           d.emplace_back(i);
           d.emplace_back(a/i);
       }
       for (int di : d) mp[di] = gcd(mp[di], a);
   }

   int ans = 0;
   for (auto [x, y] : mp)
   {
       if (x == y && x <= mn) ++ans;
   }
   cout << ans << endl;
   return 0;
}

余談です。本問題では ai  の約数が部分集合の最大公約数の候補となる。という感じで議論してきました。しかし、この約数の数ってどんなもんなんでしょう。世の中にはどうやら「高度合成数」というものがあるみたいです。厳密な定義はわかりませんが、自然数のうちその数未満の自然数よりも約数が多い数のことを言うみたいです。要はたくさん約数を持ってる数です（1や2も高度合成数ですが、、）。本問題の制約は a <= 10^9 です。10^9以下の数で、一番約数を持っている自然数（高度合成数）は「735,134,400」でその約数の個数は「1,344」らしいです。本問題では n <= 2000でしたね。仮にすべての数字が約数を1,344 個持っていたとしましょう。そうすると、2000 * 1344 でだいたい、2.5 * 10 ^6ぐらいの計算量になるのかな（約数列挙、mapの計算量がこれに加わります）。ということで、この手法で無事に計算が間に合うわけですね。

あとがき

まずは、解説記事がとっても遅くなりました。すみません。できればコンテストの次の週には書き上げたいですね。

今回のabcは問題自体が難しかったのもそうですが、どのような流れで説明するとわかりやすいか、を考えるのにとても苦労しました。とくに D 問題。難しいよ、、、それと同時に、記事を書いたことでだいぶ問題の理解が深まったといいますが、自分の考えが整理できたかなと思います。よかったよかった。

久しぶりに解説を書いたらだいぶ疲れました。ゆっくり寝ます。

最後に、、、記事内で誤りがございましたらご指摘いただけると幸いです。適宜修正いたします。本記事が誰かのお役に立てたならとっても嬉しいです。