
ABC204 C 解答
C - Tour(629)
問題
問題文
AtCoder 国には 1 から N の番号がついた N 個の都市と、1 からM の番号がついた M 個の道路があります。
道路 i を通ると都市 Ai から Bi へ移動することができます。都市 Bi から都市
Ai への通行はできません。
ピューマは、どこかの都市からスタートし、0 本以上の道路を使い移動して、どこかの都市をゴールとするような旅行の計画を立てようとしています。
スタート地点とゴール地点の都市の組として考えられるものは何通りありますか?
制約
2 ≤ N ≤ 2000
0 ≤ M ≤ min(2000, N(N−1))
1 ≤ Ai, Bi ≤N
Ai≠Bi (Ai, Bi)は相異なる
入力に含まれる値は全て整数である
考察
経路探索問題ですね。本問題はBFSやDFSなどの経路探索アルゴリズムを書けばACが貰えます。純粋な経路探索の問題はなかなかない(と思う)ので、グラフとか苦手だなー、という人は特にぜひこの問題で重たい腰を上げてみてください。少しでも理解につながるように気合入れて解説します!
今回は個人的に一番理解のしやすいBFSを説明していきます。本問題はに登場する道は一方通行ですが、まずはどちらにも通れる道を考えていきます。
アルゴリズムはとってもシンプルです。とりあえず、次のグラフを考えます。

まずは必要なものを用意します。必要なのは2つです。
1)次に探索する頂点を入れる筒
2)各頂点に到着したことがあるかどうかのメモ
です。今回は頂点0からの探索を考えてみましょう。ということで、1)の筒に0を、2)のメモの0番目を到着済み(1にする)にしましょう。これで探索の準備が整いました。

まずは筒の先頭に入っている数字を取り出してみます。今は0しかはいっていないので、当然0ですね。ということで、あなたはいま頂点0にいることにします。ここで頂点0から繋がっている(1歩で行ける)別の頂点にとりあえず移動します。
今回は1と2ですね。頂点に辿り着きましたら、到着したよということを知らせてあげましょう。メモの0を1に変更しておきます。
さて、知らせましたら次は今いる頂点たちを、1)の筒に詰めていきます。数字を入れるときは後ろから入れていき、取り出すときは前からとなります。まさしく筒ですね。
現在の状態を示します。

移動前にいた頂点を緑色で塗っています。これで頂点0からの移動はおしまいです。続きまして先ほどと同様に筒から一つ数字を取り出してみましょう。これも筒の先頭から取ってきます。
とすると、その頂点は1ですね。1から1歩で行ける頂点には2と4があります。が、2)の探索済みのメモを見ますと、どうやら2はもうすでに探索してるみたいです。ということで、今回は頂点4だけ筒に入れて、探索済みのメモに追加しておきましょう。
今のところこんな感じです。

これで、1からの探索はおしまいです。少しずつ分かってきたでしょうか?次の頂点は2ですね。同様に行いましょう。

これはどんどん繰り返します。後は図だけ貼っていきますね。

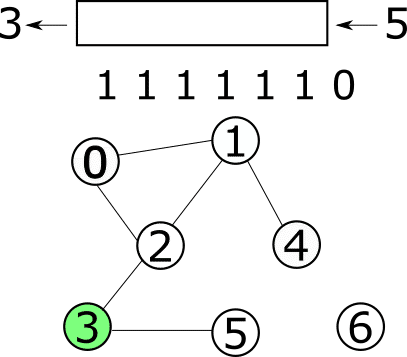

5を見たところで筒が空っぽになってしまいましたね。これが探索の終了条件です。到達済みのメモが全部埋まったらではないことに注意です。これにより頂点0から出発した際に、行くことができる頂点がすべて求まりました。今回はどんなに頑張っても0から出発していては6にたどりつけないみたいです。残念ですね。
以上がBFSの基本的な説明となります。どうでしょうか。なんとなく理解できましたか?
今回は到達できるかどうかを知りたかったのでしたね。到達済み配列の1の数が、頂点0から出発したときに到達できる数となっています。0から出発すると、0を含めて6個ですね。
今回はは頂点0から出発しましたが、これを全部の頂点から出発してみることにします。その時に得られた1の数の総和が本問題で求めたい値となります。
ただし、冒頭にも書きましたが、この説明は両方に通行できる道ですが、本問題の道は一方通行です。そこに注意です。
ここまでが、アルゴリズムおよび考察的な説明となります。
ここから、上記のアルゴリズムをプログラムで実装するために必要なことを説明します。といいましても、ソースコードを見ながらの方が良いと思いますので、必要なデータ構造だけ簡単に、、、
上記の説明で
1)筒
2)メモ
が出てきましたね。この筒にもってこいなのが、
queue:キュー
というデータ構造です。こいつは、上の説明の筒とまったく同じ挙動をします。
q.emplace(a);
と書けば、queueの後ろにaが入りますし、
q.front();
と書けば先頭の数字を取り出せます。先頭の数字を取り除きたいときには
q.pop();
を呼んであげましょう。これを使いこなせれば、BFSは楽勝です!
また、2)のメモは何でもいいです。vectorでもいいですし、配列でもいいですし、なんかおしゃれなデータ構造でも大丈夫です。到達したよ!ということがわかれば大丈夫です。
実装
#include<bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define reps(i,s,n) for(int i=s;i<n;++i)
using namespace std;
using ll = long long;
using P = pair<int, int>;
int main()
{
int n, m;
cin >> n >> m;
vector<vector<int>> g(n);
rep(i, m)
{
int a, b;
cin >> a >> b;
--a, --b;
//a->bの道を作る(一方通行)
g[a].emplace_back(b);
}
ll ans = 0;
rep(i, n)
{
//到達済みのメモ。始めは-1にしておく(0でもOK)
vector<int> used(n, -1);
//筒
queue<int> q;
//筒に頂点を入れる。メモを到達済みにする。
q.emplace(i);
used[i] = 1;
//到達済みのタイミングで答えを+1する。
++ans;
while (!q.empty())
{
int s = q.front();
q.pop();
//sにつながっている頂点がeに入る
for (auto e : g[s])
{
//到達済みならスキップする
if (used[e] == 1) continue;
used[e] = 1;
q.emplace(e);
++ans;
}
}
}
cout << ans << endl;
return 0;
}あとがき
グラフの構築に2次元vectorを使っています。グラフの作りかたは大きく2種類あると思います。
1)N*Nの配列を用意して、i, j が繋がっていればtrue、つながっていなければfalse
2)vectorをN行分用意して、i 番目がjと繋がっていたら、i 番目のvectorに要素 j を付け加える
今回は2)の方で実装しています。といいますか、グラフのほとんどはこちらになりますね。1)だと配列がとっても大きくなってしまいます。
また、今回の問題では到達できるかどうかの判定でしたので、到達済みメモを0と1で記述していました。これを、スタート地点からの距離としてあげると、各頂点までの距離が求まります。本問題の制約でしたら、距離を求めることも簡単にできますので、本問題が解けた次のステップにいかがでしょうか。
もうちょっと、複雑なグラフになるとダイクストラ法とかワーシャルフロイド法とかが登場しますが、それは先のお話です。まずは、本問題でBFSをマスターしましょう。
この記事が気に入ったらサポートをしてみませんか?
