ABC197 E 解答

E - Traveler(1379)

問題文

数直線上にボール 1 からボール N までの N 個のボールがあります。ボール i は座標 X_i にあります。各ボールには 1 以上 N 以下の整数で表される色がついていて、ボール i の色は整数 C_i で表されます。
今座標 0 にいるあなたは、毎秒 1 の速さで数直線上を動き、全てのボールを回収してから再び座標 0に戻ります。このとき、ボールの色を表す整数を回収順に並べた時に広義単調増加となっている必要があります。
ボールを回収するにはボールと同じ座標にいる必要がありますが、ボールを回収できる時に必ずしも回収する必要はありません。
座標 0 を出発してから、全てのボールを回収して再び座標 0に戻るまでにかかる時間の最小値を求めてください。

制約

1 ≤ N ≤ 2 × 10^5
|X_i| ≤ 10^9
X_i ≠ X_j (i ≠ j)
X_i ≠ 0
1 ≤ C_i ≤ N
入力に含まれる値は全て整数である

考察

まずは、色（数字）を考えたくないので、全部同じ色だったとします。

このとき、最短距離として考えられる動き方は次の2つしかありません。

右端を取得したのち、左端を取る。

左端を取得したのち、右端を取る。

これ以外は、端のボールを取る途中で必ず通るため、考慮する必要がありません。ですので、同じ色のボールにおいてはその右端と左端のみを考えましょう。

同じ色のボールを全て取ることができました。ですので、次に色を一つ進めます。各色に対して、右端と左端のボールの位置を記憶しておきましょう。次の色では前回の右端もしくは左端のうち最後に取得した方の場所がスタート位置になります。同様に、右端、左端に行き、その後逆側に行きましょう。ボールが一個しかない場合は右端と左端が一致してると考えれば良いです。

こんな感じで、最後のボールまで取って行きます。

この問題はさながら、アイテムを取りながらダンジョンをどんどん進んでいく問題とでも言えるのではないでしょうか。そのときの最短距離を求めます。

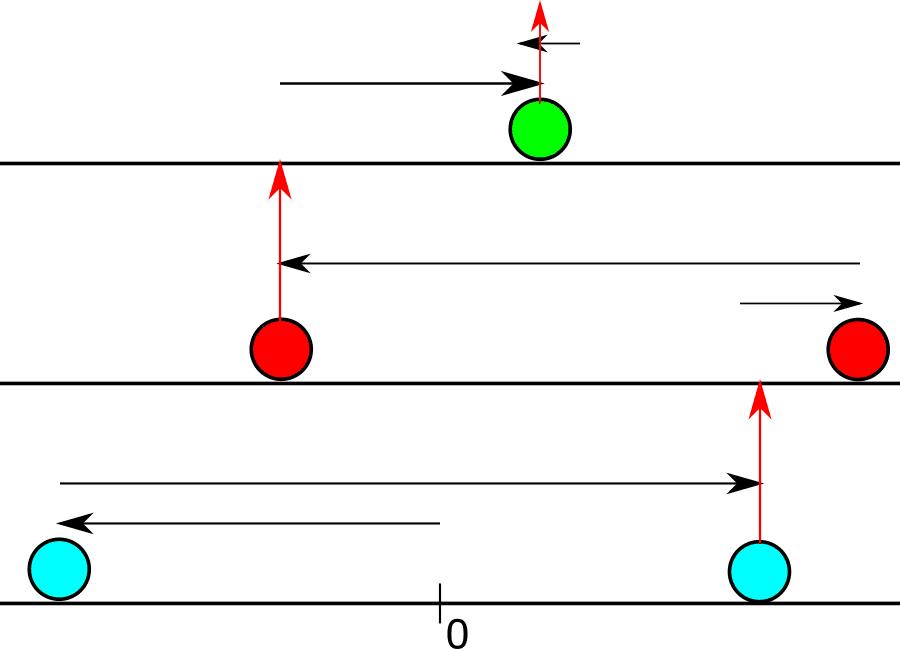
さてこのときの移動距離の最小値をdpを使って求めます。構成はこんな感じです。

dp[i][(0 or 1)] :
 i の色まで取り、
その終点（最後に取った方）が右端 : 0もしくは左端 : 1
のときの最小値

です。このdpを行うために、各色における右端配列 R と左端配列 L を用意しましょう。これらを用いて移動距離を計算してみます。

I 番目は左端で終わり i+1 番目も左端で終わる

abs(L[ I ] - R[ I+1 ]) + abs(R[I+1] - L[ I+1 ])

１項目が開始点から右端までの距離、２項目が右端から左端（終点）までの距離です。ここで、右端が開始点よりも左に存在する場合も考慮してabsの絶対値により距離を取っています。

（右端が開始点よりも左にある場合）

次に I 番目は右端で終わり i+1 番目は左端で終わる 場合です。

abs(R[ I ] - R[ I+1 ]) + abs(R[I+1] - L[ I+1 ])

L[I]がR[I]に変わりました。でもそれだけです。

これらを使うとdpは次のように更新されます。

dp[i+1][0]
= min(dp[i][0] + abs(L[i] - R[i+1]),
dp[i][1] + abs(R[i] - R[i+1]))
+ abs(R[i+1]-L[i+1]);

共通部分はminの外に出しました。dpの前状態とi+1番目における距離の和が小さい方にi+1番目の右端から左端までの距離を足したもので更新します。

上記は左端で終わる場合でしたが、右端で終わる場合も同様に考えると

dp[i+1][1]
 = min(dp[i][0] + abs(L[i] - L[i+1]),
dp[i][1] + abs(R[i] - L[i+1]))
+ abs(R[i+1]-L[i+1]);

このようになります。あとは色を小さい順に見ていき、全ての色を取り終わったらそれが答えになります。ただし、最後には0に戻ってくる必要がありますので、最終地点（右端、左端）から原点までの距離を足すのを忘れないようにしましょう。・

考察は以上です。

上でも述べましたが、dpにおいてLとRの配列を使っています。これは、まず、

pair<色番号、距離>

という配列を作って、ソートします。そうすると色の小さい順になります。あとは、mapにて同じ色の出現を監視しながら、色がなければL、Rにpushして、すでにある場合には、L、Rを更新します（距離でもソートされるのでRのみの更新で十分）。dpを回す際にはボールの個数 N ではなく、このL,Rのサイズで回すようにしましょう。

実装です。

実装

#include<bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define reps(i,s,n) for(int i=s;i<n;++i)
using namespace std;
using ll = long long;
using P = pair<int, int>;

int main()
{
   int n;
   cin >> n;
   vector<pair<ll,ll>> cx;
   vector<ll> L = {0},R = {0};
   rep(i,n)
   {
       int c,x;
       cin >> x >> c;
       cx.emplace_back(c,x);
   }
   sort(cx.begin(),cx.end());
   map<ll,bool> used;
   for(auto cxi:cx)
   {
       ll ci,xi;
       tie(ci,xi) = cxi;

       if(!used[ci])
       {
           L.emplace_back(xi);
           R.emplace_back(xi);
           used[ci] = true;
       } 
       else
       {
           int idx = L.size()-1;
           L[idx] = min(L[idx],xi);
           R[idx] = max(R[idx],xi);
       }
   }
   int s = L.size();
   vector<vector<ll>> dp(s+5, vector<ll> (2));
   dp[0][0] = 0;

   rep(i,s)
   {
       dp[i+1][0] = min(dp[i][0] + abs(L[i] - R[i+1]),
                        dp[i][1] + abs(R[i] - R[i+1]))
                        + abs(R[i+1]-L[i+1]);
       dp[i+1][1] = min(dp[i][0] + abs(L[i] - L[i+1]),
                        dp[i][1] + abs(R[i] - L[i+1]))
                        + abs(R[i+1]-L[i+1]);
   }
   ll ans = min(dp[s][0]+abs(L[s]),dp[s][1]+abs(R[s]));

   cout << ans << endl;
   return 0;
}

あとがき

実装において、L,Rの0番目の要素に0があった方がdpがシンプルになるなと思ったので、そのようにしています。dp[i]としたとき、i番目(1インデックス)のボールを取り終わった、と考えるとわかりやすいかもしれません。i = 0なら0番目のボールですので、一個もボールを取っていません。