
ABC196 F 解答
F - Substring 2 (2274)
問題
0, 1 からなる文字列 S, T が与えられます。
T が S の部分文字列となるように、Tのいくつかの文字を書き換えます。
少なくとも何文字書き換える必要がありますか?
制約
S, T は 0, 1 からなる
1 ≤ |T| ≤ |S| ≤ 10^6
考察
本問題はFFT(高速フーリエ変換)を用いて解きました。しかし、本記事ではFFT内部の具体的な説明をほとんどしません。「こんなことができる魔法のアルゴリズム」という扱いで進めます。実装もAtCoderのACLを用います。ですので「FFTはわからん。でもFが解きたい」という方には本記事がお役に立てると思います。一方で「FFTを詳しく知りたいんだ!」という需要には応えられませんのでご容赦ください。
本記事は
1. FFTで何ができるか
2. FFTをどのように問題に使うか
の流れで説明をしていきます。
まずは、
FFTで何ができるか
です。FFTは行列の掛け算(畳み込みと呼べばいいのか、内積と呼べばいいのか)を素早く行える魔法のアルゴリズムです。行列は線形代数や数学Cなどで出てくると思います。と言いましても、用語名は今回大切じゃありません。なにができるかです。
2つの行列(配列)を用意します。この行列の同じインデックスの要素の掛け算の和を求めたいとします。これを、愚直にやりますと要素分の回数計算する必要がありますね。

ここでFFTが登場します。このアルゴリズムでは内部でとても賢い計算することでこの計算を高速に行うことが可能です。ただし、掛け合わせる数は同じインデックスではなく、先頭と末尾、先頭+1と末尾-1のようにクロスしたものになります。

クロスしているのであれば、片方を逆順にしておけば同じインデックスの掛け算(縦の掛け算)が実現されます。

ここでの結論として、
FFTは行列のクロスの掛け算の和を高速に求める魔法のアルゴリズム
ということにしておきます。本問題ではこの機能を用いて問題を解いていきます。
以上がFFTの説明です。続きまして
FFTをどのように使うか
について説明していきます。
まずは本問題を計算量を考慮せずに解いてみましょう。次の例を使います。
1010001
1110
いくつか数字を書き換えて上の一部分と一致させれば良いです。これは上と下で不一致のものを数えていけば良さそうです。先頭から全部試してみましょう。

書き換えの最小値は左上の 1 回ですね。これが答えです。ただし、計算量はO((|S|-|T|+1) * |T|)です。制約を考えると間に合わなさそうです。高速化しましょう。
先に説明したFFTがここの高速化を担ってくれます。具体的には「異なる場所は何個あるか?」の部分が速くなります。ただ、このままですとFFTが使えませんので、少し変形しましょう。
まずは簡単にできるやつです。片方の配列を逆順にしましょう。
1110 → 0111
これにより、掛け算がクロスではなく縦で計算できるようになりました。
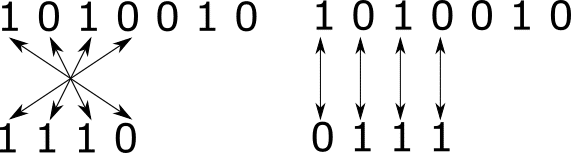
上の図は同じ計算を意味しています。
次に掛け算をつかって 0 と 1 が異なる場所の数を数え上げる方法を考えます。このまま掛け算をしてしまうと、各数字に関して
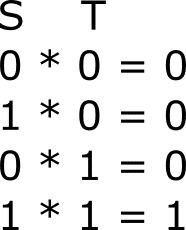
こうです。これだと、全然判定できていません。これを(0,1), (1,0)のように異なるときに 1 になるようにしたいですね。そうすれば、その和が異なる場所の数になり、その計算にFFTが使えます。
そのために、まず S の 0,1 を反転してみましょう。

なんかいい感じになりましたね。S=0 で T=1 のときのみ検出できています。今度は逆に T を反転させてみます。
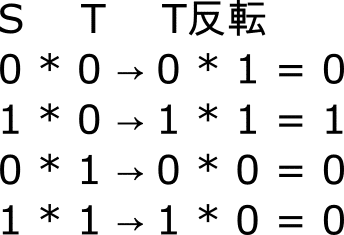
こうすると、先ほどとは逆に S=1 で T=0のときに検出できています。
この2つを組み合わせればなんか良い感じで計算ができそうです。
まとめてみます。
S(Sの一部分) と T のうち異なる数の場所を数えたい!
数が異なるのはS_i=0,T_i=1、または、S_i=0,T_i=1のとき。
これらを別々に数える。
FFTを使うために、T(または S)を逆順にする。
S を反転して FFT。 これで S=0,T=1の数 D1 がわかる。
T を反転して FFT。 これで S=1,T=0の数 D2 がわかる。
D1+D2が異なる場所の数
T をずらして同じことを行う。
それらのうちのD1+D2の最小値が答え。
考察は以上です。
実装に関してすこし述べます。
実装ではFFTにACLの convolution を用います。こちらは、配列 X と Yを入力すると、上記のFFTを行ってくれます。さらにいうと、「Tをずらす」という操作も全て行ってくれます。ですので、convolutionの結果は Tをずらした全ての値が配列に格納された状態で返ってきます。とっても便利です。(厳密な計算過程はおそらく違うと思いますが、結果として「Tをずらす」ものが全て返ります。)
ただし、注意点として配列の先頭( 0 番目)から格納されるわけではありません。インデッククス |T|-1 から |S|-1 に順番に入っていきますので、取り出すときには要注意です。後ろから |S|-|T|+1 個取り出すと間違いがないと思います。
実装
#include<bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define reps(i,s,n) for(int i=s;i<n;++i)
using namespace std;
#include <atcoder/all>
using namespace atcoder;
using ll = long long;
using P = pair<int, int>;
int main()
{
string s,t;
cin >> s >> t;
reverse(t.begin(),t.end());
int n = s.size(), m = t.size();
//何個異なっているかを記録
vector<int> d(n-m+1);
//S反転とT反転で2回行う。
rep(bit,2)
{
vector<int> x(n),y(m);
//片方の0,1を反転
rep(i,n) x[i] = ((s[i]-'0') ? !bit: bit);
rep(i,m) y[i] = ((t[i]-'0') ? bit:!bit);
//FFT
vector<int> conv = convolution(x,y);
//convの結果は後ろに格納される
//(m-1からn-1に格納される)
rep(i,d.size()) d[i] += conv[m-1+i];
}
int ans = *min_element(d.begin(),d.end());
cout << ans << endl;
return 0;
}あとがき
今回初めてACLを使いましたが、とっても便利ですね。「あるアルゴリズムを拡張させてなにかしてください。」みたいな問題だとアルゴリズム内部の理解が必要ですが、本問題のように利用するだけであれば、非常にありがたいライブラリですね。Eでも書きましたが、アルゴリズムを「入力に対して特定の出力が得られる箱」とみなすことができます。これが、車輪の再発明を避ける。ってやつでしょうか。
現段階ではACLを使うだけですが、もうちょっと強くなったらきちんと理解して自分でライブラリを書こうと思います。何年後になるのかわかりませんが、、、こつこつと強くなります。
これでABC196の全問題の解説はおしまいです。今回は難易度の傾斜が滑らかで、とっても理想的なコンテストだったのではないかと思います。私はまだまだ弱いので、難しい問題は全部難しい、と一括りにしてしまいます。そのなかでも出題のレベルを見極めていろんな参加者が楽しめる問題を配置してるのは、ただただ「凄いなあ」と感じます。
本記事が皆様の「強くなる」の一部になれたら大変嬉しいです。「強くなる」以外にも「楽しく問題を解く」「問題が解けて嬉しい」などの一部になっていたらもっと嬉しいです。長くなりましたが、ここまで読んでいただきありがとうございました。来週も頑張って記事を書こうと思います。
この記事が気に入ったらサポートをしてみませんか?
