ABC203 E 解答

E - White Pawn（1750）

問題

E - White Pawn

問題文

N を正の整数とします。 行と列にそれぞれ 0 から 2N までの番号が付いた
(2N+1)×(2N+1)のマス目があり、行 i かつ列 j に属するマスを ( i, j )で表します。
白のポーンが 1 つあり、最初(0, N)に置かれています。 黒のポーンは M 個あり、i 個目の黒のポーンは (Xi, Yi) に置かれています。
白のポーンが(i, j)にあるとき、あなたは以下のいずれかの操作で白のポーンを動かすことができます。
・0 ≤ i ≤ 2N−1, 0 ≤ j ≤ 2N を満たし、(i+1, j)に黒のポーンが無いならば、白のポーンを(i+1, j) に動かす。
・0 ≤ i ≤ 2N−1, 0 ≤ j ≤ 2N−1を満たし、(i+1, j+1)に黒のポーンが有るならば、白のポーンを(i+1, j+1)に動かす。
・0 ≤ i ≤ 2N−1, 1 ≤ j ≤ 2Nを満たし、(i+1, j−1)に黒のポーンが有るならば、白のポーンを(i+1, j−1)に動かす。
黒のポーンは動かすことができません。
この操作を繰り返した結果、(2N, Y)に白のポーンが置かれている状態にできるような Y の値としてあり得るものの個数を求めてください。

制約

1 ≤ N ≤ 10^9
0 ≤ M ≤ 2×10^5
1 ≤ Xi ≤ 2N
0 ≤ Yi ≤ 2N
(Xi, Yi) ≠ (Xj, Yj) ( i ≠ j )
入力は全て整数である。

考察

一番上の行の真ん中から出発して、一番下まで到達したときに、その到達点の個数を求めます。問題文では移動に関する条件が３つ書かれていましたね。それらをまとめますと、起こりうる状況は次の４つになります。

下２つはまとめてもいいかもしれませんね。これを上から下まで行うと答えは求まるのですが、制約が厳しそうです。盤面の大きさは最大で2*10^9もあるそうですので、間に合いません。工夫します。

まず、注目すべきは上の図の中の左上の図です。白いポーンは黒いポーンがない限り直進ができますね。もう少し付け加えますと直進しかできないのです。右下や左下に自由に動かれると組み合わせが多くなってしまいますが、そんなこともありませんので、黒いポーンがおかれていない行は省略しても答えに影響はありません。消しちゃいましょう。

とすると、考えなければいけないのは黒いポーンがある場所ということになります。黒いポーンは最大でも2*10^5個ですので、これなら間に合いそうです。

ここで以下のようなデータを導入します。

現段階において列 i に到達可能

これを最後の行まで計算して、到達可能なマス目の数を出力すれば答えです。ですので、黒いポーンの場所にてどの列に移動できるのかを判定してあげましょう。

黒いポーンがある行を X 、列を Y としましょう。ここで、黒いポーンがあるマスの一つ前に行（X-1）に注目しましょう。まず、

１）黒いポーンがある列と同じ列は到達不可能になる。

です。これは上のほうの図の右上ですね。ポーンがあったら下には降りられません。ですので、到達可能列のデータから Y を消してあげましょう。

２）黒いポーンの右上、左上から黒いポーンに到達できる

これは、左下、右下の図ですね。どちらか片方でもあれば到達が可能となります。ですので、Y-1かY+1が存在していたら、到達可能列データに Y を加えます。

これを、全部のポーンに対して上にあるものから順番に計算していけば最終到達可能な列が求まります。

ただし、ここで注意です。以下の図を考えましょう。

列に番号を振っておきました。ここで、0にある白いポーンは下に移動できますので、0はそのままにしておきます。次に１の黒いポーンは左上の0列に到達可能となっているため、1列目にも到達ができますね。到達可能列に加えておきましょう。続きまして、2列目の黒です。図では1にはポーンがいないので、到達はできませんね。ただし、先ほど1列目の判定にて1列目が到達可能列に入っています。ですので、2列目も到達可能という判定になってします。これでは正しい答えが得られません。

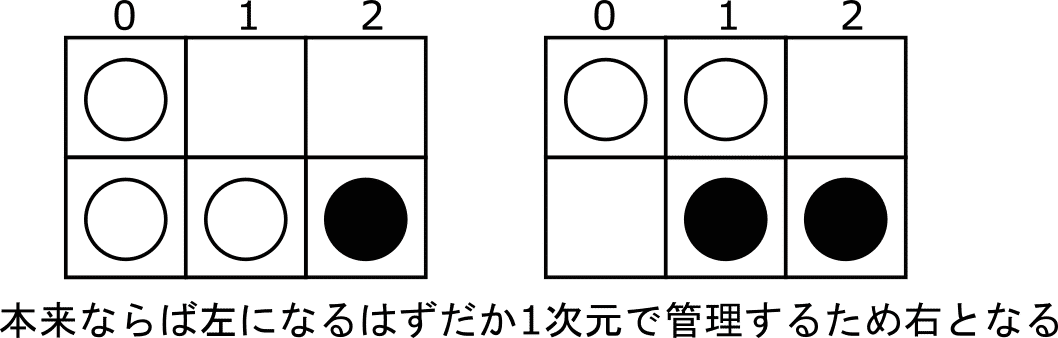
1列目の黒いポーンの判定終了時の到達可能列

ということで、値を更新するのは各行の全てを判定し終わってからにしましょう。それまでは、消す列と加える列に値を留めておきます。

また、更新するときは

消す列→加える列

の順番でやりましょう。どちらにも含まれる場合その列は到達可能です。後に消してしまうと、なくなってしまいます。

考察は以上です。

実装に関して少しだけ補足です。今回、到達可能列の管理にはsetを用います。setは重複を許さない集合で値の検索がO(log N)で可能です（Nは要素数）。便利ですね。

値を加える：insert
消す：erase
検索：count

これらの3つの操作を覚えておきましょう。

また、ソートをするために本実装ではmapを用いています。mapはキーの小さい順に値が入りますので、「小さい数字から」「同じ列にあるものをまとめて」取り出すことが可能となります。これも便利ですね。

実装

 #include <bits/stdc++.h> #define  rep(i,n) for(int i=0;i<n;++i) #define  reps(i,s,n) for(int i=s;i<n;++i)
using namespace std;
using ll = long long;
using P = pair<int, int>;

int main() 
{
   int n, m;
   cin >> n >> m;
   map<int,vector<int>> XY;
   rep(i, m)
   {
       int x, y; cin >> x >> y;
       XY[x].emplace_back(y);
   }
   set<int> ans;
   ans.insert(n);

   for (auto [ignore,XYi] : XY)
   {
       //加えるもの
       vector<int> add;
       //消すもの
       vector<int> era;
       for (auto y : XYi)
       {
           //黒ポーンの左上、右上に到達可能なら黒ポーンにも到達可能
           if(ans.count(y-1) || ans.count(y+1))
           { 
               add.emplace_back(y);
           }
           //黒ポーンの列には直進できない
           era.emplace_back(y);
       }
       //各行判定後に更新する
       for (auto e : era) ans.erase(e);
       for (auto a : add) ans.insert(a);
   }
   cout << ans.size() << endl;

   return 0;
}

あとがき

本問題ではまず盤面でなく、黒いポーンに注目することが大切でした。あとは、ポーンのマスで判定をしていけば答えが求まりました。

この問題も結局はdp(動的計画法)なのでしょうね。マス目が小さければ、各マスに対して到達可能、不可能を管理すれば答えが求まります。ですが、それが厳しいので、dpをインライン化してポーンの場所だけを更新しています。2次元dpを1次元にしていますので、循環参照が発生して、正しく更新できなくなります。ということで、更新は後でまとめて行うわけです。

シンプルながらdpの細かな点まで考えさせられる良い問題でした。