
ABC196 D 解答
D - Hanjo (1277)
問題文
縦 H メートル、横 W メートルの長方形の部屋があります。
この部屋に 2 メートル × 1メートルの区別できない畳 (長方形のタイル) A 枚と、1メートル × 1メートルの区別できない半畳 (正方形のタイル) B枚を敷き詰めます。2メートル × 1メートルの畳は縦長にも横長にも使うことができます。敷き詰める方法は何通りあるでしょうか?
なお、2A+B=HWであることが保証されます。 また、回転や反転を行うことで初めて一致するような敷き詰め方は区別します。
制約
入力は全て整数
1 ≤ H, W
HW ≤ 16
0 ≤ A,B
2A+B = HW
考察
本記事では、BFS(幅優先探索)による解法の説明をおこないます。BFSとはいいますが、やっていることは公式解説のDFSとほとんど同じです。ですので、解説見てなんとなくイメージは掴めたけど、再帰関数の実装で困ってしまうという方は、まずは、再帰関数を必要としない本記事のBFSを試してみてはいかがでしょうか。
考察始めます。一旦BFSは置いておき、問題文を整理します。
まず、制約に注目をします。
HW ≤ 16
ですので、畳をおくスペースは最大でも16マスしかありません。16マスでしたら、
各マスに畳が
置かれている:1
置かれていない:0
を全てのマスに関して 0, 1 で管理しても
2^16 = 65536 〜 6.0 * 10 ^ 4
程度の計算回数で扱えます。この0, 1のビット列と畳の関係は次の図のようになります。

i 行 j 列は、w*i + j 番目のbit に対応します。
これで、現在畳が置かれている状況というものを管理できました。この情報を持ちながら、左上から順番に畳を置いて行きましょう。
各マスについて、畳は 3 通りの置き方があります。
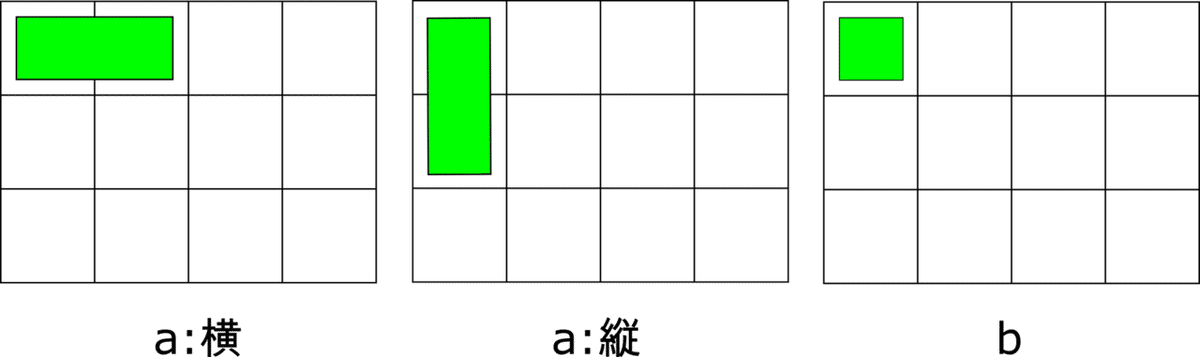
畳をおいたら、対応するマスのbitを 1 にしてあげましょう。
b : i, j (w*i + j)マスのbitを1にする。
a横: i, j (w*i + j)と i, j+1 (w*i + j+1)のマスのbitを1にする。
a縦:i, j (w*i + j)と i+1, j (w*(i+1) + j)のマスのbitを1にする。
その後、次のマス(j+1)に同様に畳を置いて行きます。端まできたら次の行の0列目に移動します(i+1, j=0)。これを、右下(i=h-1,j=w-1)に達するまでおこないます。
ただし、畳を置くことができない場合も存在します。

上記のような場合には畳を置けませんので、おとなしく別の畳をおくか、次のマスに移りましょう。
問題の説明は以上です。ここからBFSの構成について説明していきます。
BFSを行う際に持つ情報は次の通りです。
hi : 畳を置くマスの行
wi : 畳を置くマスの列
ai : 使用済みの A の畳の数
bi : 使用済みの B の畳の数
bit : 現在の畳が置かれている状態(bit列で管理)
以上の5つです。(hi, wi)で畳を置くマスの座標を表しています。
BFSは queue に
(0,0,0,0,00...)
を入れた状態からスタートします。言語にもよりますが、私はtupleで無理やり詰め込みました。
探索ではqueueの先頭を取り出して、その状態から上記の禁止された遷移を除いたものを、queueに詰め込んであげましょう。この辺りはソースコードのコメントアウトで補足します。
例として、下図の1回目の遷移のみ書いてみます。

パラメータ(hi, wi, ai, bi, bit)
初期状態 (0,0,0,0,000000000000)
Aを横置き:queue.emplace(0,1,1,0,000000000011)
Aを縦置き:queue.emplace(0,1,1,0,000000010001)
Bを置く:queue.emplace(0,1,0,1,000000000001)
すべてのbitが1になった(全てのマスに畳が敷かれた)状態が遷移の終了状態です。その状態が答えとして考えられる組み合わせの一つですので、++ansのようにカウントしましょう。また終了状態では、問題の条件からai = a, bi = b になっているはずです。
queueが空っぽになるまでこの操作を行います。探索が終わった際にansに書き込まれている数が答えになります。
考察は以上で終了です。あとは上記を適切に実装すればACできます。が、実装も少々ややこしいです。まだ気を抜かずに頑張りましょう。
実装
#include <bits/stdc++.h> #define rep(i,n) for(int i=0;i<n;++i) #define reps(i,s,n) for(int i=s;i<n;++i)
using namespace std;
using ll = long long;
using P = pair<int, int>;
int main()
{
int h,w,a,b;
cin >> h >> w >> a >> b;
queue<tuple<int,int,int,int,int>> q;
q.emplace(0,0,0,0,0);
int ans = 0;
while(!q.empty())
{
int hi,wi,ai,bi,used;
tie(hi,wi,ai,bi,used) = q.front();
q.pop();
//全てのbitが1(全てのマスが畳で埋まった)
if(used == (1<<w*h)-1)
{
++ans;
continue;
}
//現在のbit
int bit = 1<<((w*hi)+wi);
//その場にすでに置いてある場合。
if(used & 1<<bit)
{
//端じゃなければ、右のマス
if(wi+1 < w) q.emplace(hi,wi+1,ai,bi,used);
//端だったら、次の行の一番左
else q.emplace(hi+1,0,ai,bi,used);
//一番右下のマスだったら、上記のansの方に引っかかるため考慮しない。
}
//そのマスに畳がない場合
else
{
//bを置く場合(b個以上は置けない)
if(bi+1<=b)
{
//端でない
if(wi+1 < w)
{
q.emplace(hi,wi+1,ai,bi+1,used|(1<<bit));
}
//端
else
{
//一番下の行じゃなければ次の行
if(hi+1 < h) q.emplace(hi+1,0,ai,bi+1,used|(1<<bit);
//一番下の行だったら同じマスを返す。次の遷移でansに引っかかる。
else q.emplace(hi,wi,ai,bi+1,used|(1<<bit));
}
}
//aを置く場合(a個以上は置けない)
if(ai+1<=a)
{ //横置き
//隣のマスのbit
int rbit = 1<<((w*hi)+wi+1);
//端ではない、かつ、隣のマスに置かれていない
if(wi+1<w && !(used&rbit))
{
//そのマスと隣のマスのbitを1にする。
q.emplace(hi,wi+1,ai+1,bi,used|rbit|bit);
}
//縦置き
//下のマスのbit
int cbit = 1<<((w*(hi+1))+wi);
//一番下でない、かつ、下に畳が置かれていない
//(下に置かれることはないが説明上書いておく)
if(hi+1<h && !(used&cbit))
{
//そのマスと下のマスのbitを1にする。
if(wi+1<w) q.emplace(hi,wi+1,ai+1,bi,used|bit|cbit);
else q.emplace(hi+1,0,ai+1,bi,used|bit|cbit);
}
}
}
}
cout << ans << endl;
return 0;
}あとがき
本問題は制約が小さいため、このように全探索をしても解くことが可能です。他の方の解答をみると、辺の情報をbitで管理したり、dpやりながら重複を処理したりと、みなさん本当に賢い手法で解いています。
また、公式解説に載っていた
hw≦200
の制約下では境界情報をbitで管理したbitDPに頼ることになると思います。おそらく、、
冒頭でも述べましたが、行っている操作は公式放送で説明していたDFSとほとんど同じです。ただBFSを使うことで少々ややこしい再帰構造を避けています。そのため、「問題は理解したけど実装の問題でACできない」という場合にはまずはBFSを書いてみてはいかがでしょうか。それをDFSに書き換えることにより、本問題のさらなる理解と、再帰関数の練習にもなるかもしれませんね。
この記事が気に入ったらサポートをしてみませんか?
