
ARC104 Cの解答
ARC-C Fair Elevator の解答を書きます。問題はこちらから。
Difficulty : 2000(黄色)
今回arc初参加なのですが、過去問を見るにcで黄色レベルなの珍しいことなのかなと思います。急に難しくなったと感じたし、試験後に解説を読みながら実装しましたが、それでもとても苦戦しました。
結局dpにて解きましたので、dpを使った説明をしていきます。データセットを十分に作って判定部分を簡易化したため、アルゴリズムを理解しやすい形に実装できたかと思います。
まず問題を読んで条件を整理したのち、実装の方法について説明していきます。
問題整理
問題です。
2 n 階建ての建物があります。エレベータが1度だけ1階から2n階まで動きました。その途中で n 人が乗り降りしました。i 番目の人はai階で乗り、bi階で降りていきました。ただし、一つの階では1人乗るか1人降りるのいずれかしかありえません。
また、この n 人には以下の特徴があります。
もしもエレベータに2人以上乗っている場合、移動中に他の人が乗り降りした人数は等しくなる。
ここで、人の乗り降りの記録 a, bが与えられますが、残念なことに一部が欠落しています。また、残っているデータも誤りである可能性があります。
欠落したデータを正しく埋めることができるか、つまり残っているデータに矛盾のないような乗り降りの記録は実現できるかどうかを判定してください。
例として
(a,b) = (0,3),(1,2),(4,5)
でエレベータに乗り降りするというのは図で以下のように示せます(デクリメントしておきます)。

もしも、
(a,b) = (0,3),(-1,2),(4,-1)
のように「-1」が書いてあり、データが欠落していたら次のように表されます。

さて、条件について考えます。上の図でいうと、0→3、と1→2の部分で2つの→が被ってますので、この部分で条件が適用されます。今回他の人の乗り降り階数は、1人目は2回(2人目が1回乗り、1回降りる)、2人目は0回(誰も途中で降りてない)ですので、この例は条件を満たさない不適切な例となります。
では、条件を満たすのはどのような時なのでしょうか?
1人目が0番目で乗り3番目で降りた場合、その間の他の人の乗り降りは 3 -0 -1の2回となります(通過した回数分だけ他の人の乗り降りがある)。このとき、2人目は必ず1番目で乗り、4番目に降りなければなりません。そして、3人目は(2,5)となります。
つまり、i 番目で乗り w 先で降りる人がいる場合(i, w)、必然的に(i+1, i+w+1),(i+2, i+w+2) ... (i+w-1, i+2w-1)で乗り降りしなければなりません。それ以降は、i+2wで乗ってw2先で降りる人がいるので同様の議論を続けます。
これを、建物の頂点 2n-1 まで矛盾なく行えたのなら、乗り降り記録は実現できるということがわかります。


(0,3)が存在したら、(2,5)までは確定する。6以降も同様な議論を続ける。また、それ以降では、5までの矢印は考慮する必要がなくなる。
ということで、i 番目まで矛盾なく→が引けたよという dp[i] を使った動的計画法を適用していきます。
動的計画法の適用方法について、詳しく述べていきます。
方針としまして、上図における赤線を動かしながら探索を進めます。探索開始時、赤線は0の左にあります。
0番目の人がどこで降りるかを確認したいのですが、a, b が揃っていれば問題なく→が引けるのですが、データの欠落があるためそんなにうまくはいきません。
そのため、0番目から乗った人に対してすべての場合について→を伸ばします。つまり i 番目で乗った人をi+1, i+2, ..., 2n-1で降りると仮定して、すべての場合について試します(実際には上記条件より2wまで決定されるので、残りの回数の半分まで試せばよい)。
i番目の人がi+1で降りる場合、赤線がi+2の左側に引かれているという状況です。i+2 なら i +4の左側です。赤線は2個ずつ動きます。
赤線の左側で矛盾なく→が引ければdpテーブルをokに更新します。
その後、矛盾なく→が引けた赤線の次の人から同様の操作を行います。

さて、先ほどから「矛盾なく」と何度も述べていますが、矛盾とは何でしょうか。逆に矛盾する場合を例に挙げて説明をしていきます。先の矛盾していた例を使います。
(a,b) = (0,3),(-1,2),(4,-1)
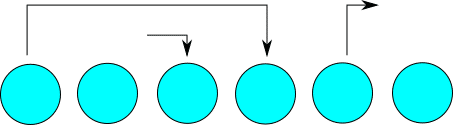
以降条件の→は下に書きます。
1、降りるべき場所で乗ってしまう。

2、乗るべき場所で降りてしまう。

3、a, bが決まっているペアが対応しない
片側が区間から出る

範囲に入っていても、違う人が乗り降りしてはいけません。
条件を変えます。

4、乗り降りの階は合ってるが人が違う
これも説明のため条件を変えます。
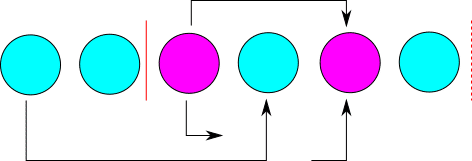
この場合、
(a, b) = (0, 3),(2, -1),(-1, 4)
という記録なので、2,4は別人が乗り降りしなければいけません。しかし、図では同一人物が乗り降りしてます。
以上の4パターンがNGとなる場合です。この条件をクリアした場合に赤線の位置を更新していきます。
ここまでが、この問題に必要な考え方です。
実装
ここから、実装に移ります。
条件の確認がしやすいようにデータセットを作っていきます。
まず、上記の条件1,2をチェックできるように、乗り降りチェック配列を作ります。
int type[n2] = -1 or 0 or 1
-1 : その階にて人が乗った
0 : 情報なし(乗っても降りてもよい)
1 : その階にて人が降りた
s で乗り t で降りるとしましょう。判定の際にtype[s] = 1 なら降りるべき階で降りているためNG、type[t] = -1も同様にNGとなります。
次に3,4をチェックできるようにペアが対応しているか、同一人物であるかを判定する配列も作ります。
p[乗る階 i (n2)][降りる階 j (n2)] = -1 or 0 or 1
-1 : (i, j)の乗り降りはしてはいけない
0 : (i, j)の乗り降り可能
1 : (i, j)の乗り降り可能かつ、i, jは同一人物
a, bが両方与えられている場合、aを固定した b 以外の j およびbを固定した a 以外の i の全てに-1 を入れておきます。これで同一人物でなくてはいけない3の条件を判定できます。
また、a, bが片方与えられている場合、片方を固定して(aとする)、type[b] が 0 じゃない部分 j は a から乗った人は降りられないので p[a][j] = -1とします。bも同様です。これで、4の条件を判定できます。
このときに、i < jの条件で十分なのでちょっと楽しましょう。
あとは、問題の入力例3にあるように、同じ数字の出現やa>=bのようなありえない条件を見張っておきましょう。
これで、説明は終わりです。以下コードとなります。
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;i++)
using namespace std;
using ll = long long;
using P = pair<int, int>;
int main()
{
int n;
cin >> n;
int n2 = n * 2;
//type[i] = -1,0,1
//-1:始点0なんでも,1:終点
vector<int> type(n2, 0);
//p[i][j] = -1,0,1
//-1,ペアにできない、0ペアok, 1ペア
vector<vector<int>> p(n2, vector<int>(n2));
//同じ数字が出てこないか見張る
bool ng = false;
//データセットを作る---------
rep(i, n) {
int a, b;
cin >> a >> b;
if (a != -1) --a;
if (b != -1) --b;
//乗り降りを記録していく
if (a != -1) {
if (type[a] != 0) ng = true;
type[a] = -1;
}
if (b != -1) {
if (type[b] != 0) ng = true;
type[b] = 1;
}
//ペアになってるもの
if (a != -1 && b != -1) {
//aとbがありえない場合
if (a >= b) ng = true;
rep(j, n2) {
p[a][j] = -1;
p[j][b] = -1;
}
//後々のために1を入れておきます。
p[a][b] = 1;
}
}
if (ng) {
cout << "No" << endl;
return 0;
}
//ペアが作れるかどうかの判定
rep(i, n2) {
if (type[i] == -1) {
rep(j, n2) {
if (type[j] == 1) {
//先ほどペアのものには1を入れておきました
if (p[i][j] == 0) {
p[i][j] = -1;
}
}
}
}
}
//データセット確認用
/*
for (auto v : type) cout << v << " ";
cout << endl;
cout << "------------------" << endl;
for (auto vv : p) {
for (auto v : vv) cout << v << " ";
cout << endl;
}
cout << "-------------" << endl;
*/
//dp回します------
vector<bool> dp(n2 + 1, false);
dp[0] = true;
//2つずつ区間をずらして判定をしていく。
for (int i = 0; i < n2; i+=2) {
if (!dp[i]) continue;
for (int j = i+2; j < n2+1; j+=2) { //n2番目まで判定するからn2+1とする
//探索の幅w先で区切れるとする。
int w = j - i;
//ペアになるので2わる。
w /= 2;
//ほんとにokか判定する(上記のデータセットを満たすか)
bool ok = true;
//w階先で降りる。
//つまり、0->w, w-1 ->2w-1でおりる
for (int k = 0; k < w && ok; ++k) {
int s = i + k; //乗る階
int t = i + k + w; // 降りる階
//ペアが確定しているもののチェック
if (p[s][t] == -1) ok = false;
//始点、終点が正しく使われているか
if (type[s] == 1 || type[t] == -1) ok = false;
}
//デバッグ用
//cout << i << " " << j << " " << w*2 << " " << ok <<endl;
dp[j] = dp[j]||ok; //一度trueになったものは、falseに更新しない。
}
}
string ans = dp[n2] ? "Yes" : "No";
cout << ans << endl;
return 0;
}判定部分を2行で記述できているので、条件チェックはしやすいのかなと思います。
実装を初めてすぐに6waまで到達したのですが、そこからが長かったです。結局、dpのtrueをfalseに上書きしてしまっている点と、2個ずつ遷移する記述を見直したらacまで行けました。
ほかの解法だと、計算速度を工夫しながらDFS(深さ優先探索)で解いている方も見受けられました。
もう、とにかく難しいですね。まず、問題の条件を置き換えながら、条件の漏れがないように丁寧に判定することが求められます。今の実力では試験時間内では解ける気が全くしません。レート2000の人はこれができるのか、と思うと驚きです。
公式解説を何度も見返したり他の方のソースコードなど色々なものを参考にしたりして、難しいなりにもなんとか理解してまとめることができました。わかってしまえば面白い問題でした。解説読んでもいまいちわからん、という方の理解の助けになればと思います。デバッグ用の出力はコメントアウトで残してあるので、参考になれば。
この記事が気に入ったらサポートをしてみませんか?
