ABC200 E 解答

E - Patisserie ABC 2（1955）

問題

E - Patisserie ABC 2

問題文

「ABC洋菓子店」で働くパティシエである高橋君は、ケーキを作って AtCoder Beginner Contest 200 を祝うことにしました。
高橋君の作るケーキは、「綺麗さ」「おいしさ」「人気度」の 3 つのパラメータをもち、それぞれのパラメータは 1 以上 N 以下の整数で表されます。
高橋君は、「綺麗さ」が i、「おいしさ」が j、「人気度」が k であるケーキを、全ての組 ( i, j ,k ) ( 1 ≤ i, j, k ≤ N ) に対して 1 つずつ作りました。
その後、高橋君は、できた N^3 個のケーキを以下の順序で並べました
・「綺麗さ」+「おいしさ」+「人気度」が小さいものを、より左に並べる。
・ここまでで順序がつかなければ、「綺麗さ」が小さいものを、より左に並べる。
・ここまでで順序がつかなければ、「おいしさ」が小さいものを、より左に並べる。
このとき、左から K 番目にあるケーキの各パラメータの値を求めてください。

制約

入力は全て整数
1 ≤ N ≤ 10^6
1 ≤ K ≤ N^3

考察

辞書順で何番目にあるかを求めます。

答えを求めるだけなら簡単です。全部書きだしてしまえばいいんです。例を見てみます。

例）N = 2, K = 7

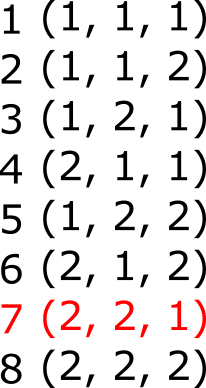
こうすると一目瞭然です。答えは(2, 2, 1)です。このようにすると、K 回計算をすれば答えが求まります。ですがこれだと間に合いませんので次にちょっとだけ工夫してみましょう。

まず、K 番目の数の合計値がいくつになるか求めましょう。数が小さいとイメージしにくいのですが、例えば、K = 10^16の場合に、その合計値が3とか4とかをしらみつぶしに調べるのはさすがに無駄が多いです。

合計値がわかりましたら、次は i (1番目の数)がいくつになるかです。計算してみるとわかるのですが、合計値がある値になるときにそれを全部調べると間に合いません。合計値が M のとなる数の値の最大は結構大きいです。ですので、i 番目だけは決定してあげましょう。

これさえ終われば、j を全探索してあげればOKです。これだけ値がそろっていれば

k = 合計値 -  i - j

と k まで決定することができます。（kが被っていますが、大文字 K と小文字 k ということで）

上記の通りに答えを求めます。まとめてみます。

１）K 番目の値の合計値はいくつになるか？
２）i の値はいくつか
３）j を全部調べる（k は一意に決まる）

次に各合計値が何個あるかを求めます。

N = 4とします。各値を図示してみます。

図のように合計値が分布します。これを k の値ごとに各合計値を並び替えてみます。

これが各合計値の個数となります。これの真ん中を見るとなんか法則性がありそうですね。はじめに全部の値（N個）を 0 にします。次に１を一つ詰めて右にシフトします。容量は４個ですので、飛び出したものは捨てましょう。次は2, 3, 4, ... と詰める数は N まで増えていき、その後減っていきます。と数字を詰めて取り出してを繰り返していけば、各合計値の値を求めることができます。

これは、queueを使うことで簡単に求めることができます。

合計値の分布が求まったら K を超えない（実装の都合上 K より小さい）値の範囲でどんどん足し合わせて、Kが出現するときの合計値を求めます。

 その合計値を X としましょう。

続いて i の値を決定しましょう。まず、各数は N までしか使えませんので、iが小さすぎると j, k を上手く設定しても合計値に達しないかもしれません。

ですので、i は

X - (N + N)

以上である必要があります。もちろん、この値は 1 以上である必要があるので、

max(X - 2*N , 1)

これが i の下限です。同様に i の上限を考えます。j, k を 1 と設定すれば、i は最大で X-2 まで大きくできます。もちろん、これは N 以下になる必要があります。ですので

min(N, X-2)

が i の上限です。この i を用いると残りの値は

X - i - 1

と表されます。これは先と同様に k=1 と設定すれば、この値分だけ任意の組み合わせが作れます（j の値を決定できればそれが組み合わせの個数になる）。ただし、各数は N までしか使えませんので、N 以上を使用している組み合わせを引きましょう。Nより大きい値がいくつあるかを求めると、それが j のとき k のときの2通りありますので、その値を*2すればＯＫです。

K を超えない（K未満）の範囲でこれを繰り返すと、i の値が決定されます。

あとは、j 以下を全探索しましょう。

以上により無事答えが求まります。あとはソースコードのコメントにて補足します。

実装

#include<bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define reps(i,s,n) for(int i=s;i<n;++i)
using namespace std;
using ll = long long;
using P = pair<ll, ll>;

int main()
{
	int n;
	ll k;
	cin >> n >> k;
	vector<ll> ijk(3 * n + 1);
	queue<int> q;
	//queueに0をn個詰め込む
	rep(i, n) q.emplace(0);
	int add = 0;
	ll sum = 0;
	bool up = true;
	//各合計値がいくつ出現するかを求める
	reps(i, 3, n * 3 + 1)
	{
		int sub = q.front();
		q.pop();
		//詰める数を変化させる
		if (up) add += 1;
		else add -= 1;
		if (add == n) up = false;
		//+ 詰めた数 - 取り出した数
		sum += max(0, add) - sub;
		ijk[i] = sum;
		q.emplace(add);
	}
	//k より小さい値に収まる範囲で
	//合計値を足していく。
	//k　番目の合計値を求める
	ll now = 0;
	int x = 2;
	reps(i, 3, n * 3 + 1)
	{
		if (now + ijk[i] < k)
		{
			now += ijk[i];
			x = i;
		}
		else break;
	}
	//合計値がx+1のときにK番目が現れる。
	//xまでにnow個出現している。
	x += 1;
	//i が小さすぎる or 大きすぎるとj,kをどのように設定しても
	//合計値が x にならない。
	for (int i = max(x - n * 2, 1); i <= min(n, x - 2); ++i)
	{
		//その i にて合計値が k となる個数を求める
		//k = 1とすればjの値を任意に変更することで
		//合計値が x となる。
		int z = x - i - 1;
		//ただし、数は N までしか使えないので
		//Nを超えた分は取り除く必要がある
		int next = z - max((z - n), 0) * 2;
		if (now + next < k)
		{
			now += next;
			continue;
		}
		//iが決定したら j を全探索。
		for (int j = max(x - i - n, 1); j <= min(x - i - 1, n); ++j)
		{
			int z = x - i - j;
			++now;
			if (now == k)
			{
				cout << i << " " << j << " " << z << endl;
				return 0;
			}
		}
	}


	return 0;
}

あとがき

辞書順の問題のため答えを求めるまでの流れはシンプルでしたが、その内容はなかなかに大変でした。

特に、各合計値の分布を求める部分は色々な考え方があると思います。公式解説ではdpを用いてその値を求めています。どうするのが簡単なんでしょうか。

私の場合、図といいますか絵を書いていたらその法則に気が付きました。この図はえびまさんの動画で紹介されていたものですので、その動画を貼っておきます。この問題のみならず各問題を数秒で解説しています。これで完全に理解するというよりかは、とりあえず見て問題の概要を掴むのにもってこいの内容となっています。

また、辞書順を求める問題は「以上」「未満」「より大きい」など、1個要素がずれてしまうということが度々起こります。ですので、実際に動かしてみてどれだけずれいるのかを修正していくのが大切だと思います。大変かもしれませんが、とにかく手を動かしてみましょう。そうすれば一歩ずつ答えに近づけると思います。