
ABC180の解答
AtCoder Beginner Contest 180を解き終わったので解答を書いていきます。問題はこちらから、
難易度はこんな感じでした。
A 0 (灰色)
B 70 (灰色)
C 89 (灰色)
D 721 (茶色)
E 1226 (水色)
F 2367 (黄色)
Dまでは抑え気味で、Fは難しめですね。しっかりと問題の解答状況で順位が決まった(早解きではない)のかなと思います。
では、書いていきます。
A box
n 個のボールが入った箱から、a 個取り出し、b 個を追加しました。さて、箱のボールは何個かな?
という問題。これは入出力と四則演算の基本の問題ですね。n, a, b がint からはみ出すこともないですので、ぱぱっと書いていきましょう。
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;i++)
using namespace std;
using ll = long long;
using P = pair<int, int>;
int main()
{
int a, b, n;
cin >> n >> a >> b;
int ans = n - a + b;
cout << ans << endl;
return 0;
}きほんの き でした。入力順だけ気を付けましょう。n, a, bの順です。
B Various distances
色々な距離を求める問題です。
数直線上に n 点の座標があります。それのぞれの座標はx1, ... , xn です。原点からこの点までの、マンハッタン距離、ユークリッド距離、チェビシェフ距離はいくつですか?
という問題。いろいろな距離が出てきますが、求め方は示してくれています。親切ですね。これも、提示された式に従って一つづつ求めていけば答えが出ます。
実装の注意点をいくつかあげます。
ユークリッド距離において x^2 を用いる。|xi| <= 10^5 なので int で処理しようとすると、オーバフローします。
ユークリッド距離は10^(-9)以下の誤差に抑える必要があるので、double で処理する。
cout << の表示桁数に限りがあるので、桁数の設定をしてあげる。
こんなもんですかね。あとは、普通に書けば大丈夫です。
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;i++)
using namespace std;
using ll = long long;
using P = pair<int, int>;
int main()
{
int n;
cin >> n;
ll am = 0;
double ae = 0;
int ac = 0;
rep(i, n)
{
ll x;
cin >> x;
x = abs(x);
am += x;
ae += x * x;
ac = max(ac, (int)x);
}
ae = sqrt(ae);
cout << setprecision(9) << fixed;
cout << am << endl;
cout << ae << endl;
cout << ac << endl;
return 0;
}cout の制限を知らなくて私はとても時間がかかりました。といいますかpythonで解きました。pythonなら上記の注意点を無視できるので、気軽に書けますね。
C Cream puff
n 個のシュークリームを分け合う問題。平等に分けれらる人数を列挙しましょう。
という問題。まず、n の約数であればシュークリームを平等に分け合えます。ということで、約数を求めます。約数は % にて剰余が 0 となる数字を見ていけば列挙できます。
この手法でO(n)で処理ができます。
しかし、問題では n <=10^12なのでそのままでは間に合いません。高速化しましょう。
約数は n を % にて演算子した結果が0になるため、/ で割っても切り捨てが起こりません。ということで、
n % i = 0 のとき n / i = j の i, jのどちらとも約数
となります。片方を求めれば相方も求まります。こうすれば√n まで処理すれば、全部列挙することができます(O(√n))。
注意点としては i = j(√n が約数)のとき、2重で列挙しないようにしましょう。if で見てもいいですし、setをかましてあげてもいいでしょう。
set を使わない場合はソートを忘れないようにしましょう。
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;i++)
using namespace std;
using ll = long long;
using P = pair<int, int>;
int main()
{
ll n;
cin >> n;
set<ll> s;
for (ll i = 1; i * i <= n; ++i)
{
if (n % i != 0) continue;
s.insert(i);
s.insert(n / i);
}
auto it = s.begin();
rep(i, s.size()) cout << *it++ << endl;
return 0;
}私はこの問題のtleがどうしても解決できませんでした。結論としては、n < 10^12 なので、for(int i = 1; i*i <= n; ++i) のなかの i * iが intに収まらず、何万回もlong にキャストしていたのが原因でした。int ではなく、 long long で宣言をしておきましょう。
追記
キャストじゃなくてオーバーフローによってfor文から抜け出せなくなっているみたい。
for(int i = 0)なんて何も考えずに書いてしまう部分なので、バグの発見が難しいかもしれません。こんな例もあるんだよ、と頭に入れておきたいですね。
D Takahashi Unevolved
進化をギリギリしないくらいでいっぱい経験値を稼ぐ問題。
ゲーム内のペットを育てていきます。はじめは強さ x で経験値 0 です。以下の2つのトレーニングで強くしていきます。
強さ *a 、経験値 +1
強さ +b 、経験値 +1
また、強さが y に到達すると進化してしまいます。進化前で一番強いときの経験値の最大値を求めましょう。
という問題。この問題で大事なのは
どちらも経験値の増加が同じ
ことですね。そのため、難しいことを考えずにどちらでもいいのでより多くトレーニングをこなしたいです。
そして、次に考えるのは足し算と掛け算の関係です。
足し算って何に足しても増加量は一緒だけど、掛け算って掛けられる数によって増加量は変わりますよね。それも、数が大きいほどたくさん増加します。
そのため、感覚的に、はじめは *a に通って、掛け算が大きくなったら +b に切り替えればよさそうな気がしてきます。実際その手法で大丈夫です。
注意点をひとつ。 x*a と x+b を比較して、x*aが大きくなっちゃたら切り替えを行います。または、x * aが進化値である y 以上になっても切り替えます。このとき、x <= y<=10^18 なので、x * a が yを大きく超えたとき、long longでもオーバーフローします。そのため、式を少し変形して
x >= y / a
このようにします。式を満たしたら切り替えることでオーバーフローに対処できます。切り替えた後は、進化までに必要な強さ - 1まで +b のトレーニングができますので、その回数を割り算で一発で求めてあげましょう。
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;i++)
using namespace std;
using ll = long long;
using P = pair<int, int>;
int main()
{
ll x, y;
int a, b;
cin >> x >> y >> a >> b;
ll ans = 0;
while (1)
{
if (x >= y/a) break;
if (x * a >= x + b) break;
++ans;
x *= a;
}
ans += (y - 1 - x) / b;
cout << ans << endl;
return 0;
}公式解説曰く、はじめの掛け算の計算はlog_a^(y) <= 64で収まるそうです。b は一回で求まるので、とっても計算量が少ない問題ですね。
最初は
dp[i] : 現在の強さ i
でdp回そうとしましたが、10^18を見てそっと諦めました。トレーニングの経験値が異なる場合にはこの手法になるのかな。
E Traveling Salesman among Aerial Cities
典型的な巡回セールスマン問題(TSP)ですね。n 個の都市をセールスマンが訪問するのですが、どういう順番で巡ると一番効率よく巡回できますか?という問題。
この問題、np困難な問題として有名なやつですね、都市の数 n が大きくなると、答えを求めるのに宇宙が消滅するまでの時間かかるってやつです。
ただし、今回は都市の最大数が 17 なので十分有限の時間で解けます。
今回は動的計画法によって解いていきます。dpの設計自体はかなりシンプルです。
dp[i][s] : 現在は都市 i にいる。sの都市を訪れた。
ときの最小コスト
ここで s は訪問済み都市の集合です。例えば都市1, 4, 8を訪問済みなら
s = {1, 4, 8}
という感じです。
次に s を用いてdpを更新します。現在都市 4 に居て、都市 7 に移動するとしましょう。s を見ます。まだ 7 は訪問してないので更新できますね。次の式で更新をしましょう。
dp[7][{1, 4, 7, 8}]
dp[4][{1, 4, 8}] + (4→7の移動コスト)
今回は最も効率よく回る方法ですので、この2式の小さいほうで更新します。とりあえずはdp自体はこれで完了です。
次にこの集合 s をなんかいい感じに表現することを考えます。
都市1つに対して、訪れた、まだだよ、の2パターンが存在するので、これをtrue, falseで考えます。true, falseって1 or 0 なので2進数で管理します。
上記の例ですと、都市の最大数を8とすると
{1, 4, 8} = 10001001
って表せます。10001001を10進数に直すと
10001001(2) = 2^7+2^3+ 2^0 = 137 (10)
ですね。ということで、s のところには137を入れておきましょう。
2進数表記だとまだまだ嬉しいことがあります。訪問済みかどうかを確認するときに都市番号番目の数字が1 or 0を見るだけで済むのです。先の例ですと、都市 7 でしたので、7 番目を見ます。と 0 なので訪問可能ということがわかります。その後、7番目に1を立てた
11001001(2) = 137 + 64 = 201 (10)
に更新をします。
本問題では n <= 17 なので、
11111111111111111(2) = 2^17-1 =131071 (10)
が最大値です。十分 int に収まりますね。
この2進数表記を用いたdpは bitdp と呼ばれる手法となります。大変便利ですね。
あとは、問題文に合うように条件を少し考えていきます(以降デクリメントして 0 インデックスとします)。
今回は都市 0 からスタートし、最後に戻ってくる必要があります。そのため、dpの開始を dp[0][1] = 0 とします。今回求めるのは最小値なので、dp[0][1]以外ははちゃめちゃに大きい数を入れておきましょう。
遷移に関しても 0 に移動する遷移を封じておきましょう(実際には、dpの更新を考えると封じる必要はありません。0 に遷移する場合 s の 0 番目に 0 がたっているはずですが、その際のコストは初期値のinfが入っているので更新されることはありません)。
あと、更新式を見るとz軸だけ少し違うので注意です。
先に述べたほうがよかったのかもしれませんが、今回の更新式であれば同じ都市に複数回訪れる必要がありません(三角不等式より)。上記の考え方は一都市一回訪問の条件で考えています。
最終的に全ての都市(8とする)を巡ることができれば
s = 11111111(2) = 255
が入っているはずです。 この時の値に、都市 0 までもどるときのコストを足して、最終的な答えを出力しましょう。
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;i++)
using namespace std;
using ll = long long;
using P = pair<int, int>;
const int inf = 1e+9 + 10;
int main()
{
int n;
cin >> n;
vector<int> x(n);
vector<int> y(n);
vector<int> z(n);
rep(i, n) cin >> x[i] >> y[i] >> z[i];
vector<vector<int>> dp(n, vector<int>(1 << n,inf));
vector<vector<int>> dist(n, vector<int>(n));
//距離計算
rep(i, n)rep(j, n)
{
int d = abs(x[i] - x[j]);
d += abs(y[i] - y[j]);
d += max(0, z[j] - z[i]);
dist[i][j] = d;
}
dp[0][1] = 0;
rep(s, 1<<n)//訪れた場所
{
rep(i, n) //今いる場所
{
rep(j,n)//次に行く場所
{
int sj = 1 << j;
if (s & sj) continue; //訪問済み
dp[j][s+sj] = min(dp[i][s] + dist[i][j], dp[j][s+sj]);
}
}
}
int ans = inf;
//0に戻るまでのコストを計算
for (int i = 1; i < n; ++i)
{
ans = min(ans, dp[i][(1 << n) - 1] + dist[i][0]);
}
cout << ans << endl;
return 0;
}今回は先に移動コストを求めておきました。あと、ビットシフトを利用して 1 がたっているかを確認しています。
今まで敬遠してましたがこれ便利ですね。ビットシフトや & のビット要素の論理積だったりと学びの多い問題でした。
F Unbranched
条件を満たすグラフは何個作れますか?という数え上げの問題。数が大きくなるので10^9+7で割った余りを出力します。
問題文を理解するのに時間がかかったので図の力を借ります。
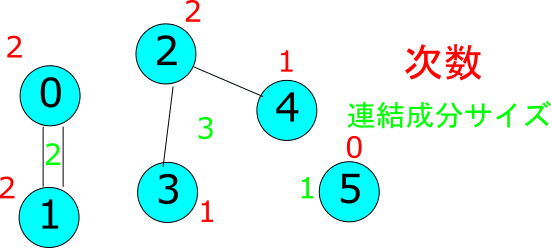
こんなグラフがあったとしましょう。n = 6, m = 4 です。問題の条件は3つありますね。
自己ループを持たない。
すべての頂点の次数が 2 以下である
各連結成分のサイズを並べたとき、その最大値がちょうど l である
自己ループってこんなやつです。持ってませんね。

次数は頂点につながってる辺の数ですね。赤色のやつです。図では全部2以下になってます。
連結成分のサイズは緑色のやつです。l = 3 なら正解ですね。
という感じで、条件を満たすものを数え挙げていきます。
とはいうものの、何から手を付けていいのか迷います。ということで、まずは、条件の言い換えをしてみましょう。
自己ループを持たない。はその通りです。ループを持たないように気を付けましょう。
次数が2以下についてです。次数が2以下だと、枝分かれを持つグラフが作れないことがわかります。あと、お互いに手を繋いだ構造からはほかの辺は作れません。

ということで、作れるグラフは以下の2種類になります。

PathグラフとCycleグラフと呼ばれるそうです。とりあえず、このグラフを作っていく限り次数の条件を破ることはなさそうです。また、手つなぎ構造は2頂点のCycleグラフとみなすことができます。
また、頂点数が n のとき、pathグラフでは n -1辺、cycleグラフでは n 辺が用いられます。あと、cycleグラフは1頂点では作れません。これらは後で使います。
最後の条件です。サイズの最大値が l になるそうですが、最大値って言われると難しいですね。グラフを考える中で、すでに l を作ったから、あと何でもいいとか、まだ作ってないからどこかで作らなくてはいけない。みたいな。常に頭の片隅に残ってると考えることが増えてしまいます。
ということで、こう言い換えます。
全てのグラフのサイズが l 以下になればよい。
こうすれば、グラフ1つ1つ考えるだけでよいです。ただし、この場合ですと、最大値を l 未満として余裕をもって数え上げる人も出てきます。ということで、求めるグラフの個数は
全てのサイズが l 以下の個数 ー 全てサイズが l - 1 以下の個数
となります。こうすれば、必ずサイズ l のものが1つは存在することになります。
条件の言い換えも終わりましたので、数え上げの方法について考えていきます。今回は再びですが dpを用いて考えていきます。設計はこうです。
dp[i][j] : i 頂点、 j 辺使った際に作れたグラフの個数
これを、上記の条件を満たしながら、n 頂点、m 辺まで回していきます。
更新について考えましょう。
現在、i 頂点、j 辺しようとしていて、次数 k のグラフを作るときを考えます。
ここで、必要となるの要素が2つあります。
pathおよびcycleグラフは何種類あるか。
重複のない頂点の選び方は何通りあるか。
まず、path, cycleグラフの種類数です。pathグラフから行きましょう。本問題では幸か不幸か頂点はそれぞれ区別します。また、pathグラフは無向グラフですが向の概念を追加すると、順列のように考えられます。pathグラフの次数が1の頂点は2つありますが、片方をスタート、片方をゴールとすれば、完全に順列ですね。
頂点番号1, 3, 5 の3つでpathグラフを作るのならば、
1,3,5
1,5,3
3,1,5
3,5,1
5,1,3
5,3,1
の6つです。要は3 !です。ただし、勝手に有向グラフにしたので、向きをなくしましょう。スタートとゴールの概念をなくせばよいので、ちょうどこの半分になります。
結局のところ、pathグラフの種類数は頂点数が n のとき
n ! / 2
となります(n >= 2)。n = 1のときは 1 です。階乗が出てくると、計算量が大変なことになるので、少し手を加えます。pathグラフの種類数を次数順に書きだしてみると
k 1, 2, 3, 4, 5, 6, ...
数 1, 1, 3, 12, 60, 360, ...
となります。よく見ると、kの数って、k-1の数 * k になってますね。この値を先に計算して配列に入れておきましょう。
次にcycleグラフです。こちらはpathグラフを利用すれば簡単です。pathグラフが順列なら、cycleグラフは円順列です。円順列の基本は一人を固定することですね。高校生の時に何度も言われました。ということで、n 頂点を持つcycleグラフの一頂点を固定しましょう。

これって、n-1 のpathグラフと同じになりませんか。そのため、cycleグラフの種類数は先に作成したpathグラフの種類数の配列を一つずらしてあげれば取得できます。
これで、グラフの種類数は終わりです。
重複のない頂点の選び方に移ります。
まず、重複があるってどういうことなのか再び図の力を借りて説明します。

グラフ 1

グラフ 2 (重複してない)

グラフ 3 (重複してる)
全部、手つなぎ1個、3つのpathが1個、1つ頂点が1個の組み合わせです。1と2は頂点番号が違うので重複ではないです。ただし、3はまったく一緒なのでダメです。「0,1と5の場所入れ替えただけじゃないか」といわれそうですね。どうして入れ替わってしまったのか説明します。
グラフ1ではまず k = 2のグラフで0, 1を使って手つなぎを作ります(i = 2, j = 2)。次にk = 3のpathを2, 3, 4で作ります(i = 5, k = 4)。最後にk= 1で1頂点のグラフを作ります(i = 6, j = 4)。
察しの良い方ならもうわかると思いますが書いていきます。
グラフ3ではまず k = 1のグラフで5を使って1頂点のグラフを作ります(i = 1, j = 0)。次にk = 3のpathを2, 3, 4で作ります(i = 4, k = 2)。最後にk= 2で0, 1頂点の手つなぎグラフを作ります(i = 6, j = 4)。
こうなってしまうんですね。だから重複が生まれます。
重複を防ぐために、
残っている頂点の中から最も若い番号の頂点を1つ用いる
というルールを設けます。こうすれば、グラフ3のように、はじめに5の1頂点グラフを作るということが防げます。
このルールの下で、頂点番号の組み合わせの個数を考えましょう。
通常、n 個のうちからk 個選ぶ際には n_C_k でよいのですが、最も若い頂点は必ず選ばれるので、選択の余地が1つだけ狭まります。n-1, k -1 にしましょう。あとは、n個あればいいのですが、もう既に頂点は i 個使っていますので、結局のところ、
n - i - 1 _ C _ k-1
が組み合わせ数となります。Cの計算も大変ですね。今回は先にパスカルの三角形を用意しておくので、そこから値を取ってきます。
さて、色々と条件やらを求めました。この条件を使ってdp の更新は次のように行われます。
頂点数 k のグラフを追加する。
dp[i+k][j+k-1 or j+k] += dp[i][j] * 種類数(path,cycle) * 頂点の選び方
↓
dp[i+k][j+k-1 or j+k] += dp[i][j] * path[k] or cycle[k] * (n - i - 1 _ C _ k-1)
pathグラフならj+k-1, cycleグラフなら j+k になります。
ここまで非常に長かったですが、あと1点ほど。
冒頭に書きましたが答えは非常に大きくなるので、都度modで抑える必要があります。path数やパスカルの三角形もです。dpの更新式なんて、大きいやつらの掛け算なんで大変です。オーバーフローしないように掛け算を分けたり、long longにキャストするなりして対処しましょう。
#include <bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;i++)
#define reps(i,s,n) for(int i=s;i<n;i++)
using namespace std;
using ll = long long;
using P = pair<int, int>;
const int mod = 1e9+7;
int f(int n, int m, int l)
{
//種類数の計算
vector<int> path(l+1,0), cycle(l+1,0);
path[1] = 1;
if (l >= 2) path[2] = 1; // l=1のとき対策
reps(i, 3, l + 1) path[i] = ((ll)path[i - 1] * i) % mod;
reps(i, 2, l + 1) cycle[i] = path[i - 1];
//頂点の選び方の計算
//パスカルの三角形を用いる
vector<vector<int>> p(n + 1, vector<int> (n + 1));
p[0][0] = 1;
rep(i, n)rep(j, i + 1)
{
p[i + 1][j] += p[i][j];
p[i + 1][j] %= mod;
p[i + 1][j + 1] += p[i][j];
p[i + 1][j + 1] %= mod;
}
//dpテーブル
//dp[i][j]: i個頂点を使った。j個辺を使った。
vector<vector<int>> dp(n + 1, vector<int>(m + 1, 0));
dp[0][0] = 1;
//dpを回す
rep(i, n)rep(j, m+1)
//追加辺 j が0でも、頂点だけ追加できるのでjはmまで、
{
//pathの追加
reps(k, 1, l+1)
{
int ni = k + i;
int nj = k + j - 1;
if (ni > n || nj > m) break;
/*
一気に掛けるとオーバフローするので都度modを取る
やっていることは
dp[ni][nj] += dp[i][j] * cycle[k]* p[n - i - 1][k - 1] % mod;
dp[ni][nj] %= mod;
*/
ll add = ((ll)path[k] * p[n-i-1][k-1]) % mod;
add = (add * dp[i][j]) % mod;
dp[ni][nj] = (dp[ni][nj] + add) % mod;
}
//cycleの追加
reps(k, 2, l+1)
{
int ni = k + i;
int nj = k + j;
if (ni > n || nj > m) break;
/*
一気に掛けるとオーバフローするので都度modを取る
やっていることは
dp[ni][nj] += dp[i][j] * path[k]* p[n - i - 1][k - 1] % mod;
dp[ni][nj] %= mod;
*/
ll add = ((ll)cycle[k] * p[n - i - 1][k - 1]) % mod;
add = (add * dp[i][j]) % mod;
dp[ni][nj] = (dp[ni][nj] + add) % mod;
}
}
return dp[n][m];
}
int main()
{
int n, m, l;
cin >> n >> m >> l;
int ans = f(n,m,l) - f(n,m,l-1);
if (ans < 0) ans += mod;
else ans %= mod;
cout << ans << endl;
return 0;
}pathとcycleおよび三角形は一度求めれば使いまわせるので、関数f( )の外で求めて使いまわしたほうが早いです。しかし、計算時間に余裕があるのでできるだけ説明に沿った記述にしてます。
あと、modについて補足をば。10^9+7という数はちょこちょこ見ますがちゃんと意味があるそうです。
素数である。
10^9+7未満の足し算は int に収まる。
10^9+7未満の掛け算は long longに収まる。
という感じです。今回は「掛け算がlong longに収まる」というところが問題で、要はint からはみ出すよということです。そのため、long longにキャストする必要があります。また、掛け算はlong longに収まりますが、掛け算の掛け算は収まりません。本問題をpythonでも実装したのですが、pythonのint は64bit ですので、それすらも飛び越えてオーバーフローして大変でした。(bit 数って指定できるんですかね?)
追記
python3系だと制限はないっぽいですね。でもなんで、答えが合わないんだ?
更に追記
どうやら、mod の宣言の際にmod = 1e9+7とやるとfloat型になってしまうようです。それで割るとその値もfloatになってしまって、制限に引っかかっていました。modをintに明示的にキャストしたら無事正しく動いてくれました。
pythonは型を指定しなくても上手いこととやってくれる便利な言語ですけど、気を付けましょうということで。
最近は逐一modを取ってくれる、modint というライブラリが人気みたいですね。mod を気にして実装するのは大変だし、何よりミスが多発するので、私も導入したいですね。
解説は以上です。
Fは難しかったですが、Eまでは手を付けれた方も多かったのではなのでしょうか。私はCすらダメでしたが、、
あと、AからFまで書くと、ABCといえども非常に長くて読むの大変ですね。私が見返す際にも大変困っています。とはいっても、問題ごとに分けると、Aなんかは「Twitterかな」っていう分量になってしまうので、悩みどころですね。
この記事が気に入ったらサポートをしてみませんか?
