
ABC197 F 解答
F - Construct a Palindrome (1945)
問題文
N 頂点 M 辺の、単純とは限らない連結な無向グラフがあります。
辺 i は頂点 A_i と頂点 B_i を結んでおり、文字 C_iが書かれています。
頂点 1 から頂点 N へのパス (同じ辺や頂点を複数回通っても構わない) を 1 つ選び、通る辺に書かれている文字を順に並べて文字列を作ります。
この文字列が回文になることはあるかを判定し、あるならばそのような回文の長さとして考えられる最小値を求めてください。
制約
2 ≤ N ≤ 1000
1 ≤ M ≤1000
1 ≤ A_i ≤ N
1 ≤ B_i ≤ N
C_iは英小文字
与えられるグラフは連結である
考察
まずは回文について考えましょう。回文は
abcdcba
xyzzyx
のように、前から読んでも後ろから読んでも同じ文字列になるものを言います。ではどうやって回文を作るのでしょうか?前側から
a
ab
abc
abcd
のように構成していってもできなくはないのですが、少々扱いが難しいです。文字列の長さを幾つにするか?次になんの文字を入れればいいか?よくわからなくなります。ですので次のように前後1セットで考えてみます。
a a
ab ba
abc cba
abcdcba
こうすると、とりあえず前後に同じ文字列を詰めていくだけで簡単に回文が完成します。
ここまで、なんの話だ?となったかもしれませんが、この考え方がこの問題で大切になります。本問題ではグラフ上にて頂点1からNまでのあるルートをたどることで回文を構成します。これをスタートから順番にやっていくと、あまりにも選択肢が多すぎてよくわからなくなります。同じ道を通ることが可能ですので、選択肢は無限かもしれません。

ですので、先ほどの2番目の方法をとります。回文を前側と後ろ側から同時に構成していきましょう。具体的には頂点1と頂点Nから同じ文字が書かれた辺を辿っていきます。
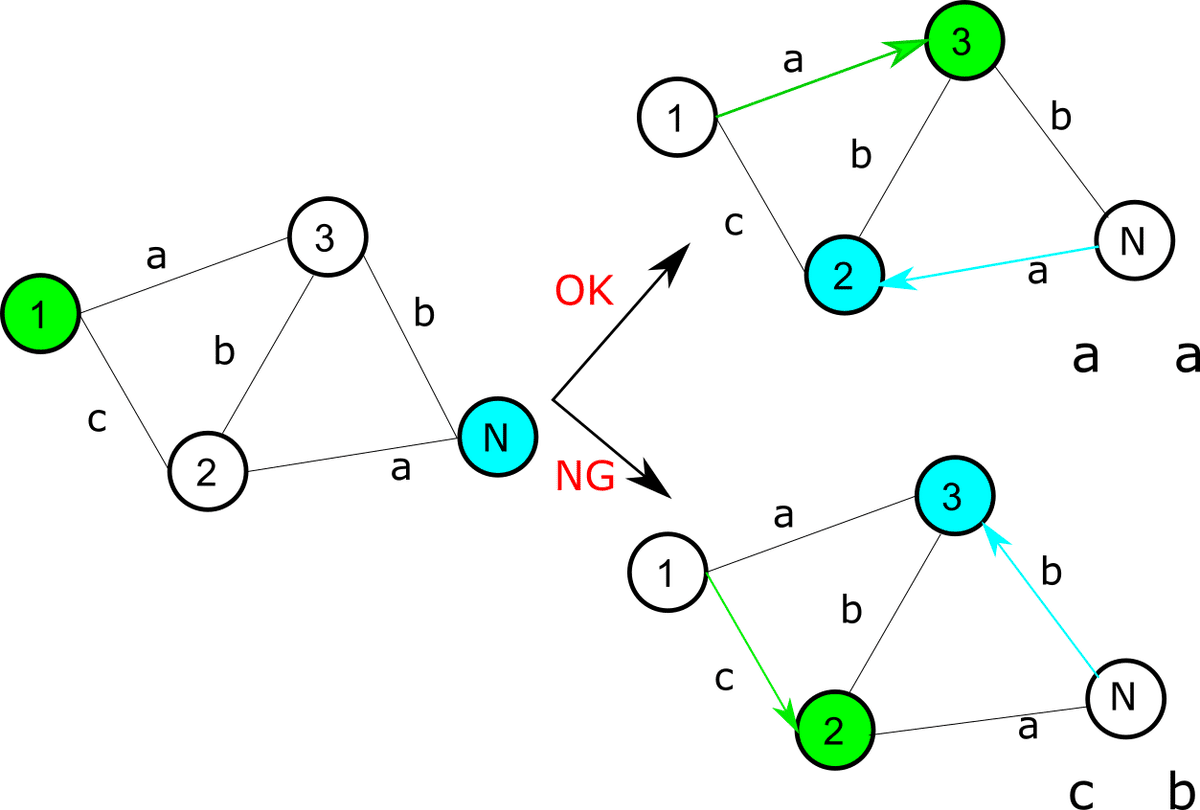
(同じ文字の辺を辿っていくと回文が完成する)
このようにすると回文が完成するのですが、2つのマスを同時に考えるのは少々大変です。これらをまとめる方法を考えます。
上の図で前側と後ろ側の場所をセットで管理してみます。
スタート (1, N)
次状態 (3,2)
こんな感じです。ですので、この状態を頂点に持つグラフを作ってみましょう。このとき同じ文字を持つ場合に辺の移動ができた(図のOKの場合)ので、同じ文字の場合にのみグラフに辺を追加してあげましょう。これを2乗のグラフと呼ぶことにします。

上記のグラフにおいて(1,N)から探索をスタートします。本問題ではBFS(幅優先探索)にて解いてあげます。
次にどうすれば回文が完成するか(BFSの終了条件)について考えます。本記事冒頭で例を出しましたが、回分には
abcdcba
のように奇数長のものと
xyzzyx
のように偶数長のものがあります。
2乗のグラフにおいて偶数長になるのは、(A,B)のA = B となるときです。元のグラフで考えると、前側と後ろ側が同じマスにあるときです。これは回文になりそうですね。またその長さは辺を移動した数の2倍です。
奇数長となるのは、元のグラフにおいて1つの辺で移動できる頂点に前側と後ろ側が存在する場合です。2乗グラフでいうと
(2, 3)
の場合ですね。この判定には元のグラフの辺のつながりを見てあげましょう。元のグラフにおいて頂点2と結合している頂点に3が含まれているかをチェックしましょう。もし含まれていたら奇数長の回文が作れます。そしてその長さは、辺を移動した数の2倍+1です。
最後にBFSの構成について述べます。次のようなqueueを用いました。
queue<tuple<int,int,int>>
int : 前側から移動した頂点
int : 後ろ側から移動した頂点
int : 移動した回数
です。これをtupleで管理してあげましょう。
考察は以上です。本問題も実装が大変なので、コメントで補足していきます。
実装
#include<bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define reps(i,s,n) for(int i=s;i<n;++i)
using namespace std;
using ll = long long;
using P = pair<int, int>;
int main()
{
int n,m;
cin >> n >> m;
//元のグラフ
//繋がっている頂点番号
//辺に書かれている文字
vector<vector<P>> g1(n);
//2乗のグラフ
//繋がっている頂点番号(前側)
//繋がっている頂点番号(後ろ側)
vector<vector<vector<P>>> g2(n, vector<vector<P>> (n));
//グラフの構成
rep(i,m)
{
int a,b;
char c;
cin >> a >> b >> c;
--a;--b;
//数字に変換
g1[a].emplace_back(b,c-'a');
g1[b].emplace_back(a,c-'a');
}
//2乗のグラフの構成
rep(ai,n)rep(bj,n)
{
//前側頂点に繋がっている頂点
for(auto eci:g1[ai])
{
int ei,ci;
tie(ei,ci) = eci;
//後ろ側頂点に繋がっている頂点
for(auto ecj:g1[bj])
{
int ej,cj;
tie(ej,cj) = ecj;
//前側と後ろ側の文字が一致している
if(ci == cj)
{
g2[ai][bj].emplace_back(ei,ej);
g2[ei][ej].emplace_back(ai,bj);
}
}
}
}
//大きな値を入れておく
const int INF = 1e9;
int ans = INF;
//頂点をすでに通過済みかを監視
vector<vector<int>> used(n,vector<int> (n));
queue<tuple<int,int,int>> q;
//初期状態を入れる
q.emplace(0,n-1,0);
while(!q.empty())
{
int x,y,cost;
tie(x,y,cost) = q.front();
q.pop();
//偶数長
if(x==y) ans = min(ans,2*cost);
//奇数長
for(auto yi :g1[x])
{
if(y == yi.first) ans = min(ans,2*cost+1);
}
for(auto xyi:g2[x][y])
{
int xi,yi;
tie(xi,yi) = xyi;
//通過済みかどうかを判定
if(used[xi][yi]) continue;
used[xi][yi] = 1;
//距離を+1してqueueにいれる
q.emplace(xi,yi,cost+1);
}
}
//もし回文が作れなかったら-1
if(ans == INF) ans = -1;
cout << ans << endl;
return 0;
}あとがき
計算量について書きます。
2乗のグラフを構成しますとさらっと書きましたが、計算量は大丈夫かをみていきます。このグラフを構成する際には頂点AとBから出ている辺の数の掛け算だけ辺が出現します。そして、頂点A、Bはとりうる全ての組み合わせに関して考慮する必要があります。そのため、なんだかとっても多くなりそうですね。ただし、全ての頂点から出る辺の総数は問題文からM 本となります(Mが2頂点を結ぶため、2Mと考えても良いかも)。そのため、最大のケースにおいてもその計算量はO(M^2)で抑えられ、制約より10^6程度になります。
BFSの計算量は次の通りです。
各頂点はqueueに高々1回だけ挿入される。
各辺は高々1回だけ探索される。
ので、頂点 N、辺 Mとした場合にその計算量はO(N+M)になります。このくらいなら間に合いそうですね。よかったです。
本問題では2乗のグラフを構成しましたが、これ賢いですね。使ったことがある、慣れていないと、なかなかこの発想はできないです。こういう問題はやはり経験がものをいうのでしょうか?色々な問題を解いて、様々な解法をインプットしたいですね。
これでABC197の解答はおしまいです。少しお恥ずかしいのですが、コンテスト後に解答を読んだら、うわ解けたなー、と思う問題が多かったです。特にDとE。ただ、問題が解けるという状態とテストで得点できる状態には大きな差があると高校の頃の先生が言っていました。まさしくこれです!
解ける!からACまでのそのギャップを埋めるためには、めげずにコンテストに出場するのが一番の近道だと思いますので、これからもレートの冷えに負けずに参加します!
ここまで読んでいただきありがとうございました。この記事が誰かのお役に立てたのならとっても嬉しいです。
この記事が気に入ったらサポートをしてみませんか?
