
ABC199 F 解答
F - Graph Smoothing(2065)
問題文
N 頂点 M 辺の単純無向グラフがあります。頂点には 1 から N までの、辺には 1 からM までの番号がついています。辺 i は頂点 Xi と頂点 Yi を結んでいます。また、頂点 i には最初整数 Ai が書かれています。
あなたは K 回にわたって以下の操作を行います。
・M 本ある辺の中から、一様ランダムかつ他の選択と独立に 1 本選ぶ。その辺が結ぶ 2 頂点に書かれている数の平均を x として、その 2 頂点に書かれている数を両方 x で置き換える。
各頂点 i について、K 回の操作後に頂点 i に書かれている数の期待値を求め、注記の通り mod( 10^9+7 )で出力してください。
注記
有理数を出力する際は、まずその有理数を分数 y / x として表してください。ここで、x, y は整数であり、 x は 10^9+7で割り切れてはなりません (この問題の制約下で、そのような表現は必ず可能です)。
そして、xz ≡ y ( mod 10^9+7 )を満たすような 0 以上 10^9 + 6
以下の唯一の整数 z を出力してください。
制約
2 ≤ N ≤ 100
1 ≤ M ≤ N (N−1)/2
0 ≤ K ≤ 10^9
0 ≤ Ai ≤ 10^9
1 ≤ Xi ≤ N
1 ≤ Yi ≤ N
与えられるグラフは単純
入力に含まれる値は全て整数である
考察
本記事では行列累乗によってこの問題を解きます。その中で、いくつかアルゴリズムといいますか、データ構造と言いますか、ライブラリと言いますか、を用います。ただ、それらを全て説明しようとすると問題の本筋の説明よりもだいぶ長くなってしまうため、説明は他の記事に任せます。ですので、ライブラリの詳しい仕組みを知らなくても解くことができるように説明をしてきます。各ライブラリに「何を入力して」「何が得られるか」を理解していれば大丈夫です。というよりか、それがライブラリのあるべき姿だと思います。とはいえ、完全に丸投げしてしまうと、この問題の理解が遠のいてしまうので、冒頭で使用したライブラリを簡単に紹介します。こんなやつらが登場するんだな、ぐらいの認識で大丈夫です。
アルゴリズム、ライブラリ
1)modintライブラリ(なくてもOK)
その都度modをとってくれる優れもの。
後述の逆元により割り算にも対応
2)逆元
ax≡1 (mod)における x
問題の注記に使用。
3)繰り返し2乗法
A^Bを高速に解いてくれる。
4)行列累乗(高速化)
繰り返し2乗法を行列に適用したもの。
だいたいはこの4つです。興味がありましたら調べてみてください。
さて、問題解説に移ります。本問題はなかなかに工程が多いですので次のような章立てに従って説明をしていきます。ちょっと長いですが、これを読んでいけばACにたどり着けるように頑張って書いていきます。
1)何をする問題か?
2)遷移情報の確認
3)行列表現
4)行列(分子)の行列累乗
5)分母の繰り返し2乗法
6)注記の操作(逆元)
以上6工程です。お付き合いくださいませ。いきます。
1)何をする問題か?
例として次のようなグラフを考えます。

このときにある辺が1つ選ばれます。その辺に繋がっている2つの頂点に書かれた数字がそれらの平均になってしまいます。

行われる操作はこんな感じです。これをK回繰り返していきます。
しかし、本問題ではどの辺が選ばれるかの指定はなく、K回操作後の「期待値」を求めることになります。まずここが難しいポイントの1つ目です。
2)遷移情報の確認
この章では「期待値」をどのように扱っていくかを説明していきます。ちょっと長いですが、この問題の問題らしい部分ですので、具体例から一般例という流れで説明をします。
1)にてどの辺が選ばれるかわからないという話をしました。これは、逆に言えばどの辺も等しい確率で選ばれるわけです。この考えが大事です。
これを考慮に入れて、1回操作した後の頂点に書かれている数字の「期待値」とやらを求めてあげます。
上記グラフの4の頂点に関して見ていきます。グラフを見てみると選ばれる辺によって、4がどのように変化するかが異なることがわかると思います。「期待値」というものを考えるために、本来ならば1本しか選ばれないところを、3本全部選んでみます。ただし、1本あたりの影響力は1/ 3としておきましょう。
1)4の頂点に連結している辺が選ばれる(赤以外)
4はその頂点とつながっている頂点との平均になる。
2)4の頂点に連結していない辺が選ばれる(赤)
4のまま変化しない
です。このときそれぞれの影響力は
1)
4-8の辺:(4+5) / 2 * (1 / 3) = 9 / 6
4-8の辺:(4+8) / 2 * (1 / 3) = 12 / 6
2)
4 / 3
です。1)は辺ごとに異なりますね。1)は4の頂点とつながっていない辺が多いほど、その影響力は大きくなります。2)になる確率が上がるとでも言いましょうか。
ですので、1回操作した時の4の頂点の期待値は
9 / 6 + 12 / 6 + 4 / 3 = 29 / 6
となります。約分しなかったのはここで計算するためです。こんな計算を全ての頂点に対して行いますと、1回やった期待値が求まります。
さて、次はこれをちょっとだけ一般化しましょう。

Aは頂点に書かれている数字、Dはその頂点につながっている辺の数です。頂点の数は4としましょう。
先ほどと同様に1回操作した時の変化を書いていきます。また変化後の各数字をA'としています。
追記
20210608
画像の数式が誤っていたため4点を差し替えました。以下*のついている画像は差し替え後のものになります。差し替え以前の画像は本記事末尾に掲載しています。
*1

あまりにも見にくかったので数式に起こしました。これをちょこっと変形します。

*2

式の中の1/2+1/2の部分は結局 D1 個になるので、まとめてしまいました。他の頂点でも全く同じ計算でこんな感じの式に変形することができます。
この形式ってまさにDPですね。前状態から次の状態への遷移が表されています。いわゆる漸化式というやつです。これを全ての頂点に対してK回行えば、”あくまで”答えは求まります。ここからもう一工夫必要ですが、この問題の核となる部分はこれで十分です。
3)行列表現
2)で動的計画法(DP)を使えば解けそうというところまで来ました。が、制約を見ると操作回数はどうやら10^9らしいです。このままではちょっと間に合いません。ですので、高速化を考えます、そのために、全ての遷移情報を書き出してみます。
*3

流石に全部を式で出すのは心が折れました。手書きで許してください。
この形を見るとなんか行列で表せそうですね。

こんな感じで1回の遷移はこのような行列で表現されます。じっと見つめていると次のような法則が見られます。
1)左上から右下までの対角線:2M(M-Di)+Di
2)頂点がつながっている:1
3)つながっていない:0
今後の都合上 1/2Mは外に出しておきました。
4)行列(分子)の行列累乗
獲得された行列を使って遷移を高速化しましょう。
ということで、行列を使って2回ぐらい遷移させてみましょうか。

ということで、2回遷移させる操作は行列(と2M)を2乗したものと掛け合わせることに等しくなります。ということは、これをK乗したものとA1~A4を掛け合わせればK回操作した時の答えが求まります。
このような手法は行列累乗と呼ばれます。すべてのDPがこうできるわけではありません。あくまで線形な遷移に限られます。よくある、「条件を満たしたら遷移する」みたいなやつは非線形ですので、この方法では解けません。
あとはこの計算を高速化するだけです。高速化には行列の繰り返し2乗法を用います。この記事では詳しくは説明しませんが、2乗の計算を早くやってくれます。
まいどお馴染みの典型問題に任せます。
ちょっとだけ説明しますと、例えばAの100乗なら通常は100回ループが必要です。しかし、
A^100 = A^64 * A^32 * A^4
となることを利用して、あらかじめ、A^1,A^2,A^4,A^8,...を計算しておけばすごく早く累乗が計算できるよ、という方法です。pythonのpowなんかはデフォルトでこのアルゴリズムが採用されているはずです。C系もそうなのかな?
高速化まで合わせて行列累乗と呼ばれるのでしょうか。あまり詳しく知りません。が本問題ではこちらの方法により計算をします。
5)分母の繰り返し2乗法
都合により、行列部分の分子と分母の部分を分けました。注記の通りに出力する都合上少数にできないからしょうがないです。
とにかく今は(2M)^K を求めます。といいましても、やることは4)と同じです。繰り返し2乗法をやってあげましょう。
私が一瞬で繰り返し2乗法を理解した方法を少しだけ、、
100乗であったら、100を二進数で表すと、
1100100
ですね。右からA^1と対応してるとしましょう。これらのうち1が立っている部分をかけていけば無事繰り返し2乗法の完成です。これだけです。偶数なら/2奇数なら−1みたいなことをするよりも理解しやすいかと思います。
6)注記の操作(逆元)
5)までで、行列が求まりましたので、A1~A4までを掛け合わせれば答えが出てきますが、出力は注記の方法に従わなければなりません。
計算した結果の分母と分子という言葉を用いるならば
分母*Z≡分子(mod 10^9+7)
を成立させる、Zということになります。ここでは逆元という考え方を用います。詳しくはこちらからお願いします。難しい概念ですが、大変わかりやすく説明されています。
本当に簡単にだけ説明します。
逆元はあるmod M にて、X*Zの余りが1となるZのことを言います(まったく厳密ではありません)。
5にZを掛けたら 1 になります。
Zは何でしょう?
1/5です。
これは逆数ですね。
は馴染みがあると思います。これと同じ感じです。逆元の例はリンクの解説記事に載ってます。
ですので、逆元を求めるライブラリを使ってあげると
分母*Z ≡ 1 (mod 10^7)
を満たす Z が求まります。mod 空間で掛け算をしても答えは変わりませんので、両辺に分子をかけましょう。先ほどと同じ式ですね。
ということで、分母の逆元に分子をかけたものが答えになります。
これを、全頂点分出力してあげれば晴れてACがもらえます。
大変長かったですが、あとは実装するだけです。ライブライを多く使っているので長くなっていますが、本質の部分だけ見れば十分に理解できると思います。
実装
#include <bits/stdc++.h> #define rep(i,n) for(int i=0;i<n;++i) #define reps(i,s,n) for(int i=s;i<n;++i)
using namespace std;
using ll = long long;
using P = pair<int, int>;
//modint ライブラリ
const int mod = 1e9 + 7;
class mint
{
public:
long long x;
mint(long long x = 0) :x((x% mod + mod) % mod) {}
mint operator -() const { return mint(-x); }
mint& operator +=(const mint a)
{
if ((x += a.x) >= mod) x -= mod;
return *this;
}
mint& operator -=(const mint a)
{
if ((x += -a.x + mod) >= mod) x -= mod;
return *this;
}
mint& operator *=(const mint a)
{
(x *= a.x) %= mod;
return *this;
}
mint operator+(const mint a)
{
mint res(*this);
return res += a;
}
mint operator-(const mint a)
{
mint res(*this);
return res -= a;
}
mint operator*(const mint a)
{
mint res(*this);
return res *= a;
}
mint pow(long long t) const
{
if (!t) return 1;
mint a = pow(t >> 1);
a *= a;
if (t & 1) a *= *this;
return a;
}
//for only prime number
//Fermat's little theorem
//逆元
mint inv() const
{
return pow(mod - 2);
}
mint& operator/=(const mint a)
{
return (*this) *= a.inv();
}
mint operator/(const mint a)
{
mint res(*this);
return res /= a;
}
};
//行列の構造体
struct Matrix
{
int s;
mint A[100][100];
};
//行列計算
Matrix cal_matrix(Matrix X, Matrix Y)
{
int s = X.s;
Matrix Z = {s};
rep(i,s)rep(j,s) Z.A[i][j] = 0;
//xとyのサイズが同じとする
rep(i,s)rep(j,s)rep(k,s)
{
Z.A[i][j] += X.A[i][k]*Y.A[k][j];
}
return Z;
}
//行列の繰り返し2乗法
Matrix matrix_pow(Matrix X,ll n)
{
Matrix table[64];
Matrix An = X;
//A^(2n)を計算
for(int i = 0;i<64;++i)
{
table[i] = An;
An = cal_matrix(An,An);
}
//基本行列
Matrix I = {X.s};
rep(i,X.s)rep(j,X.s)
{
if(i==j) I.A[i][j] = 1;
else I.A[i][j] = 0;
}
if(n == 0) return I;
//繰り返し2乗法
for(int i = 0;i < 64;++i)
{
if(n & (1LL<<i)) I = cal_matrix(I,table[i]);
}
return I;
}
//繰り返し2乗法
mint pow_mod(mint x,int n)
{
if(n == 0) return 1;
mint table[64];
for(int i=0;i<60;++i)
{
table[i] = x;
x = x*x;
}
mint res = 1;
for(int i = 0;i < 64;++i)
{
if(n & (1LL<<i)) res *= table[i];
}
return res;
}
bool g[100][100];
int main()
{
int n,m,k;
cin>> n >> m >> k;
vector<int> A(n);
rep(i,n) cin >> A[i];
//頂点の次数
vector<int> D(n);
rep(i,m)
{
int a,b;cin >> a >> b;
--a,--b;
g[a][b] = true;
g[b][a] = true;
++D[a],++D[b];
}
Matrix F;
F.s = n;
//行列の作成
//分子だけ計算する
rep(i,n)rep(j,n)
{
if(i==j)F.A[i][j] = 2*(m-D[i])+D[i];
else
{
if(g[i][j]) F.A[i][j] = 1;
else F.A[i][j] = 0;
}
}
//繰り返し2情報で行列累乗
F = matrix_pow(F,k);
//分母の計算
mint x = 2*m;
x = pow_mod(x,k);
//累乗した行列に対して計算する
mint Y[100];
rep(i,n)
{
rep(j,n)
{
Y[i] += F.A[i][j]*A[j];
}
}
//分母の逆元に分子をかける
rep(i,n)
{
cout << (x.inv()*Y[i]).x << endl;
}
return 0;
}あとがき
ライブラリのせい?おかげ?ですが説明が長ければコードもとても長いですね。先にも書きましたが、まずはライブラリはそういうもんだ、と開き直って適切に使用できていれば問題ないと思います。自分のアルゴリズム力が上がって、再び向き合ってみたらすんなり理解できる。そんな日がいつか来るはずです。正直私も、modintや逆元を完全に理解してるとは言い切れません。
ですが、やっていることを順序立てて処理していけば決して理解できない内容ではないと思います。登場するアルゴリズムは、どれも「水色までに必要なアルゴリズム」で紹介されてたと思います(行列累乗はどうだったけ?)。ですので、基本的と言っていいのか知りませんが、扱いやすいアルゴリズムを適切に組み合わせて問題を切り崩していくという非常に綺麗な問題だったのではないかなと思います。実際、解説を読みながらですが、一つ一つ紐どいていく感じは楽しかったです。
これでABC199の解説はおしまいです。私はF問題で考察を考えている時よりもD問題にて実装をしている時の方が苦戦をしました。全体的に難しかったと思います。皆様はどう感じたでしょうか。
ここまで非常に長くなりましたが、読んでいただきありがとうございました。記事中で分かりにくい表現、間違えている点、不明点などありましたら、コメントでもTwitterでもなんでも大丈夫ですのでおしらせください。この記事が皆様の理解をほんの少しでも担ってくれたらとても嬉しいです。次はABC200でお会いしましょう。
追記
20210608
差し替え前の画像を次に掲載しておきます。記事内の画像は訂正済みのものになります。
*1

*2
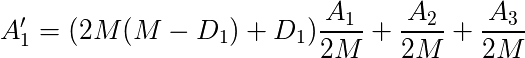
*3

*4

この記事が気に入ったらサポートをしてみませんか?
