ABC201 E 解答

E - Xor Distances（1694）

問題

E - Xor Distances

問題文

N 頂点の重み付き木があります。i 本目の辺は頂点 ui と頂点 vi を双方向に結んでいて、その重みは wi です。頂点の組 ( x, y ) について、dist ( x, y ) を以下のように定めます。

・x から y への最短パスに含まれる辺全ての重みの XOR

1 ≤ i < j ≤ N を満たす全ての組 ( i, j ) について dist( i, j ) を求め、その総和を 
( 10^9+7 ) で割った余りを出力してください。

制約

2 ≤ N ≤ 2×10^5
1 ≤ ui < vi ≤ N
0 ≤ wi < 2^60
与えられるグラフは木
入力は全て整数

考察

まずはxor演算の性質を見ていきます。（10進数と2進数を混ぜてます。すみません）

6 xor 3
= 110 xor 011
= 101
= 5

となります。もうちょっと見てみます。

6 xor 3 xor 5 
＝(6 xor 3) xor 5
= 101 xor 101
= 0

これを縦に書いてみます。

6 : 110
3 : 011
5 : 101
     000

です。なんか言えそうなことをまとめます。

１）xor演算は各桁ごとに独立してる
２）その値は1の数の偶数奇数で決定される
３）同じもののxorは0

です。例が少なくてこじつけみたいになってますが、今一度確認してみてください。

問題に移ります。本問題は木の任意の2点を選択してその経路のxor演算の総和を求める問題です。木の具体例を示します。ついでに2進数にしておきます。

このままだと、見通しが立たないので、先の性質を使います。２）です。xor 演算は各桁ごとに独立して考えられるので、桁を分けてしまいましょう。1桁目に注目すると次のようなグラフになります。試しに2つに頂点を選んでxorを取ってみます。

となります。これを全ての頂点の組みでやったら大変なことになりそうです。

ですので、一つ基準を決めてあげましょう。その基準から各頂点への xor 演算を計算します。
その後再び、先ほどと同じ頂点のxorを考えてみます。頂点を0と置いておきましょうか。１と置いても答えは変わりません。

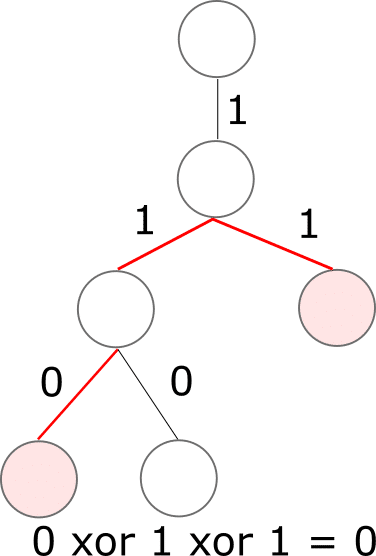
するとどうでしょうか。基準からのxorの値のxor（赤い経路）は、

先程の経路+共通の経路

というように表現されてます。ここで性質の３）です。同じもののxorは0になりますね。0 xor X = Xとなるように、0とのxorはその値が返ります。ですので、共通経路が無視されて任意の2点間のxorが取得できるわけです（水色と緑でかぶっているところは無視できる）。実際に計算してみると

基準から左下：1 xor 1 xor 0 = 0
基準から右下：1 xor 1 = 0

で1つ目の１が共通ですので、これは無視できます。とすると

1 xor 0 xor 1 = 0

となって一致します。

これを全頂点間で試して1となる組を数えれば良さそうです。が、これだと計算量はO(N^2)です。頂点数の2乗だけかかります。残念ながら間に合いません。

少し考え方を変えてみましょう。頂点を2つ選んだ時に起こりうる組み合わせを列挙します。

0 0 : 0
0 1 : 1
1 0 : 1
1 1 : 0

の4つです。このうち1となるのは10か01の場合です。ここでxorの２）です。xorは1の数の偶数奇数により決定されます。順番も関係ありませんね。

ということで、xorが1となる頂点の組みは0の頂点から1個、1の頂点から1個選んだ場合に限られます。その組の総数は、

総数＝0の頂点数*1の頂点数

で求まります。各頂点が0、1のどちらか調べるだけですので、O(N)で計算できます。上の図の場合ですと、

5 * 1 = 5 通り

でしょうか。

これで1桁目が1となる総数が求まりました。2進数の1桁目は1です。1が総数個存在することになりますので、この総数が答えに加算されます。

2桁目以降も同様に求めることが可能です。ただし、最後に答えに加算する時には注意が必要です。2進数の2桁目は2ですので、総数に2をかけたものを足しましょう。２が総数個存在するということです。3桁目なら4ですね。

以上の計算により答えを求めることが可能です。

実装について少しだけ説明します。木グラフにおいて各値のxorを求めるのはBFSやDFSでやるのが良さそうです。制約を見ますと桁は60桁あるので、BFSを60回やると全桁求まります。しかもどうやらこれが間に合うらしいです。詳しくは確かめてないです。

ですが、60回もやる必要はなく、例えば各頂点に対して60個分配列を用意して、探索の際にはビットシフトで桁をずらしてあげれば1回のBFSやDFSで探索が完了します。

あとはソースコードで補足します。

実装

#include<bits/stdc++.h>
#define rep(i,n) for(int i=0;i<n;++i)
#define reps(i,s,n) for(int i=s;i<n;++i)
using namespace std;
using ll = long long;
using P = pair<ll, ll>;

const int mod = 1e9 + 7;
class mint
{
public:
   long long x;
   mint(long long x = 0) :x((x% mod + mod) % mod) {}
   mint operator -() const { return mint(-x); }
   mint& operator +=(const mint a)
   {
       if ((x += a.x) >= mod) x -= mod;
       return *this;
   }
   mint& operator -=(const mint a)
   {
       if ((x += -a.x + mod) >= mod) x -= mod;
       return *this;
   }
   mint& operator *=(const mint a)
   {
       (x *= a.x) %= mod;
       return *this;
   }
   mint operator+(const mint a)
   {
       mint res(*this);
       return res += a;
   }
   mint operator-(const mint a)
   {
       mint res(*this);
       return res -= a;
   }
   mint operator*(const mint a)
   {
       mint res(*this);
       return res *= a;
   }
   mint pow(long long t) const
   {
       if (!t) return 1;
       mint a = pow(t >> 1);
       a *= a;
       if (t & 1) a *= *this;
       return a;
   }
   //for only prime number
   //Fermat's little theorem
   mint inv() const
   {
       return pow(mod - 2);
   }
   mint& operator/=(const mint a)
   {
       return (*this) *= a.inv();
   }
   mint operator/(const mint a)
   {
       mint res(*this);
       return res /= a;
   }
};
vector<vector<pair<int, ll>>> g;

vector<int> used;
vector<vector<int>> x;
void dfs(int s)
{
   for (auto [e, w] : g[s])
   {
       if (used[e]) continue;
       used[e] = 1;
       //各桁で計算する
       rep(i, 60)
       {
           //各辺のそれまでの値とwの各桁のxor
           x[e][i] = x[s][i] ^ (w >> i & 1);
       }
       dfs(e);
   }

}

int main()
{
   int n;
   cin >> n;
   g.resize(n);
   used.resize(n);
   x.resize(n);
   rep(i, n) x[i].resize(60, 0);
   rep(i, n - 1)
   {
       int u, v;
       ll w;
       cin >> u >> v >> w;
       --u, --v;
       g[u].emplace_back(v, w);
       g[v].emplace_back(u, w);
   }
      
   //頂点0を基準にする
   used[0] = 1;
   dfs(0);
   mint ans = 0;
   rep(i, 60)
   {
       int zero = 0;
       int one = 0;
       rep(j, n)
       {
           //０と１の数をカウントする
           if (x[j][i] == 0) ++zero;
           else ++one;
       }
       //1桁目なら1,
       //2桁目なら2
       //3桁目なら4。
       mint bit = 1LL << i;
       //オーバーフローに注意
       ans += bit * zero * one;
   }
   cout << ans.x << endl;


   return 0;
}

あとがき

xorの性質を生かした問題でした。この問題のポイントは

xorは各桁ごとに計算できること
同じ数字のxorは0となること

だと思います。この性質を上手く使うことで、木構造の探索を効率よく行っています。

この問題は解説を見れば、なるほど、となりますがなかなかコンテスト中には気がつきませんね。どんな練習をすれば解けるようになるのでしょうか。

ただ、各要素を分解していくと見たことあるものも多いです。xorは各桁で計算、交換法則がある（これにより基準からのxorで計算）、同じものは０、などなど、グラフと合わさると見えにくくなります。

考えれば考えるほど、2つの要素がいい感じに組み合わさった素敵な問題だと思います。ぜひ挑戦してみてください！