
数理最適化(線形計画問題③)
今日は非線形計画問題を線形計画問題で近似して解くということについてまとめていきたいと思います。
非線形計画問題
非線形計画問題は、非線形計画関数の最小化もしくは最大化を解く問題です。
非線形関数とは
非線形関数は、一次関数(直線)ではない関数のことです。
例えば、二次関数のような直線ではない関数です。

凸関数(とつかんすう)
二次関数のように上下どちらかに出っ張った関数です。
山形の関数を、上に凸な関数と呼びます。
上の図のように、Uの字型の関数を下に凸な関数と呼びます。
凸関数に対し、凹関数(おうかんすう)というものもあります。
「上に凸な関数」と「下に凹な関数」は同じです。
「下に凹な関数」と「上に凹な関数」は同じです。
(わかりずらい。。。)
凸計画問題
一般的に、「上に」「下に」を付けない場合は、
・凸関数:Uの字型(下に凸な関数)
・凹関数:山形(下に凹な関数)
を指すようです。
そのため、凸計画問題は、Uの字型の関数を目的関数とする問題です。
また、凸集合(※後で解説)であることが条件となります。
凸計画問題は、凸関数に対して最小化を求める問題ということになります。
凸集合
任意の二点を結ぶ線分が集合内に完全に含まれるような集合です。
y = x^2 は、Uの字の中のどの2点をとっても、必ずUの字の中に入っています。
このような集合のことを言います。
(変な出っ張りが無い関数)

上に凸な関数の最大化問題
上に凸な関数の最大化は「凹計画問題」とも言うようですが、上下逆になっているだけなのであまり変わりません。
線形計画問題への近似
分離可能(※後で解説)な凸計画問題は、線形計画問題に近似できます。
※凸ではない非線形計画関数は、別の手法で近似することができます
分離可能
分離可能とは、複数の変数があるとき、変数どおしの加減算のみで目的関数や制約条件を表現できるような関数のことを指します。
$$
y = x_1^2 + x_2^2 + x_3^2
$$
のような関数です。
関数を個々の変数に対する関数の和として表現すると、元々の非線形計画問題をより単純な形式に分解することができます。
そうすると、計算が容易になることがあります。
先ほどの関数を、下記のように表現できます。
$$
x_1^2 + x_2^2 + x_3^2 = f(x_1, x_2, x_3) = f(x_1) + f(x_2) + f(x_3)
$$
このように分割することができ、f(x1)、f(x2)、f(x3) の各々に対して独立に最適化を行い、全体の問題を解くことができる場合があります。
分離できない関数は、以下のような関数です。
$$
f(x_1, x_2) = x_1 x_2
$$
この関数は、x1とx2の積であり、変数ごとに分離することができません。
近似
1つ1つの変数ごとにばらします。
そうすると、シンプルな凸関数になります。
その凸関数上にいくつか点を取ります。
その点を直線でつなぐと、点の区間ごとの線形関数で表現することができます。
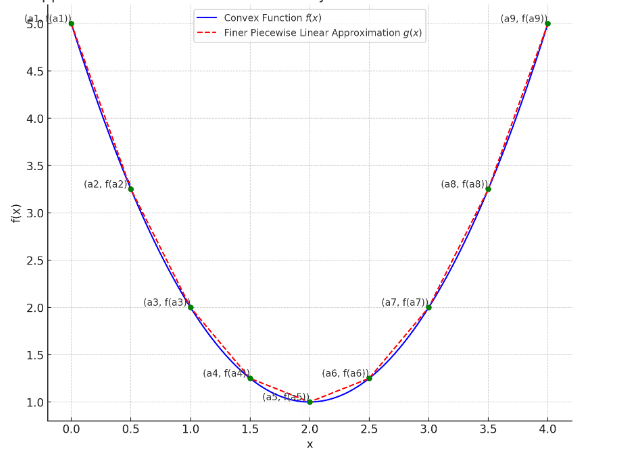
点a2と点a3をつなぐ直線の式を求めてみます。2点(x1, y1), (x2, y2) を通る直線の方程式は、
$$
y - y_1 = \cfrac{y_2 - y_1}{x_2 - x_1}(x - x_1)\\
↓\\
y = \cfrac{y_2 - y_1}{x_2 - x_1}(x - x_1) + y_1
$$
で表すことができます。
この方程式については、下記サイトがわかりやすいです。
よって、点a2と点a3をつなぐ直線は、以下のように表すことができます。
$$
y = \cfrac{f(a_3) - f(a_2)}{a_3 - a_2}(x - a_2) + f(a_2)
$$
このように、全ての点をつなぐ直線は、以下の式で表すことができます。
$$
y = \cfrac{f(a_{i+1}) - f(a_i)}{a_{i+1} - a_i}(x - a_i) + f(a_i)
$$
この凸関数の近似直線のことを、「区分線形関数」と呼びます。
区分線形関数は、いくつかの線形関数をつなぎ合わせてできた関数です。
各線形関数は、グラフ上で直線の一部を表しいます。
これらの直線が集まって一つの折れ線の形を作ります。

区分線形凸関数の最小化問題は、以下のように表すことができるようです。
$$
min f(x) = \displaystyle\max_{i=1,2…,m-1} \lbrace{\cfrac{f(a_{i+1}) - f(a_i)}{a_{i+1} - a_i}(x - a_i) + f(a_i)} \rbrace\\
a_1 \leq x \leq a_m
$$
この数式がまだよくわかっていません。
それは、「max」の意味です。
次回は、この定式の意味についてまとめていきたいと思います。
(今回まとめようと思いましたが、まだ頭の中が整理しきれていない)
この記事が気に入ったらサポートをしてみませんか?
