整数論への憧れ

＜どのようにして自然数を憶えたのか＞
ヒトは自分の姿の一部分しか知らない。まして、自分の幼少期のことなど殆ど知らない。

どのようにして「１、２、３、・・・」と数えることを憶えたのか。何が面白くて憶えようとしたのか。身近にいる幼児を観察してみると、「一から十まで」数えて喜ぶばかりか「一から百までも」喜々として数える。

喜ぶ親がいるからなのか。それとも、自然数がどこまでも続くことが嬉しいのか。自然数が続くリズムに魅了されるのか。

言葉や音楽と同じように、数そのものが何かに触れ、何かを表すと感じるからなのか。
それとも、言葉や音楽と同じように、数にはそれぞれ個性があって「１は・・・」「２は・・・」という響きがあるのかも知れない。

つまり、自然数（整数）を知りたい、憶えたいという憧れは個人的なものではなく、ヒトに共通したものとしてあるに違いない。
それにもかかわらず、オトナはそれを忘れ、憧れの自覚も、忘れたことさえ自覚していない。

＜自然数について考える＞
オトナは「１、２、３、・・・」と続く自然数について、何も憶えていない。
しかし、ユークリッド原論では、「数とは単位から成る多である」、「素数とは単位によってのみ割り切られる数である」と定義されている。

「原論」はユークリッドという人の名を冠せられてはいるが一人ではなく、数学集団が編纂したことはよく知られていることである。
また、その数学集団がすべて発見した事実を内容とするものではなく、歴史的な発見の集大成としての「原論」なのである。

一人ひとりは、どのように自然数を理解し自分のものにしたのかは分からない。しかし、系統としてのヒトは「十進記数法」　など、ユークリッド原論に始まる数論の中に、「なぜ、どのように」自然数を理解してきたのか、そのヒントを探ってきたのではないのか。

＜デジタルと自然数＞
ところで、古い文献ではデジタル（digital）の訳語は「計数」だという。
子どもが遊んでいてドングリを見つける。そして、その一つを「ひ」と呼び、隣のドングリを「ふ」と呼び、さらにその隣を「み」と呼ぶ姿が思い浮かぶ。風景の中から一つのドングリを選び取る。その行為の集積から数詞「１（ひ）、２（ふ）、３（み）」が生まれ、「三個」という概念が形成されたのではないか、と想像される。
言わば、デジタルは「１、２、３、・・・」と自然数に対応する「離散的」な、周囲を捉える表現なのである。

それに対して、夜空の流れ星は一直線に走って消える。また、月の輪郭は円から半円に変わり、三日月になる。
古代ギリシャの幾何学は星座学と源を同じにする、という説がある。つまり、幾何学は連続する自然現象を（幾何学的な）素材である直線や円弧に対応させて捉える「連続的でアナログ」な表現なのである。

「デジタル」の始原的な意味としては、周囲の現象を「離散的に捉えて」自然数に対応させる表現だ、と言っていい。

＜自然数の意義＞
そして、自然数は「１、２、３」にとどまらず、限りなく続く現象に対応して、限りなく続く表現方法を得ていく。
その一つが十進記数法である。「０、１、２、３、４、５、６、７、８、９」の十個の数詞だけを用いて、いくらでも大きな数字を表現することができる。また、いくらでも小さな数字も表現することができるようになる。

私たち一人ひとりは、どのように自然数を理解し活用してきたのか。数える時の道具に過ぎないのか。改めてその存在意義を問うてみたいのである。

系統としてのヒトは、「十進記数法」など、ユークリッド原論に始まる数論の中に、「数とは何か」という問いに対する答えを探ってきたのではないのか。
特に、自然数の中に「素数」を発見したヒトの心は、まさに現代数学者の心と同じで、自然数一つひとつには「向き合うべき背景」が存在している、と主張しているように感じる。

「１は『全体』を」、「２は『対』を」といった神話等につながる意味ではなく、宇宙や自然を捉える感触である。その感触の一端を言葉にすると、「連続性」、「無限性」、「個性」、「相互関連性」、・・・等であり、自然数はそれらの象徴的存在なのである。

＜整数論の内容＞
ユークリッド原論から数世紀が過ぎて、整数論は「素数の分布」を探る方向と、「素数相互の関係」を明らかにする方向、さらには素数を「分解してみよう」と考える「類体論」へと展開していく。

数学者ガウス（１７７７～１８５５）は、「素数の分布」については「素数定理」を発見し、「素数相互の関係」については「平方剰余法則」を発見している。
また、「類体論」の原初の形として「複素整数論」を展開した。

＜ガウスの素数定理＞
１５歳のガウスは、１７９２年に「素数の出現率」について調査する。
十以下の自然数の中に素数は四個、百以下には二十五個、千以下には
百六十八個である。その出現率は次第に減少する。
その減少傾向には何か法則があるのではないのか。
表を作りグラフにして、その減少する様子を探ってみる。

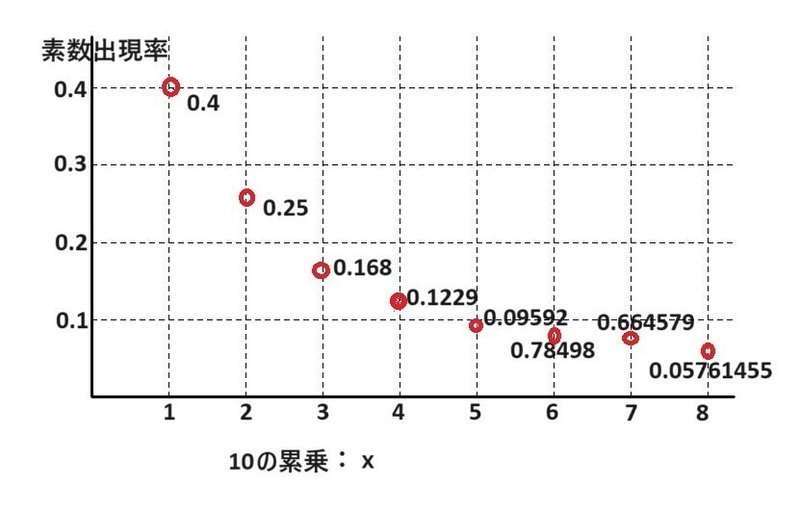
＜出現率の減少を式化する＞

出現率をｙとして、最初に思い浮かべる式は「y=0.4/x」である。
しかし、これではあまりにも急激に減少する。

そこで、出現率の変化を「十の累乗」ではなく、ネイピア数の「ｅの累乗」で表してみる。
すると、不思議なことに、素数の個数が「２の累乗」に近いことが分かる。

すなわち、「１～３」の区間に２個の素数が存在し、その「２倍」の「１～６」の区間に４個の素数が出現するのではなく、「ｅ」倍の区間「１～７」の区間に４個の素数が出現している。
これは、素数の個数が「２倍」になるためには間隔が「ｅ」倍に伸びることを意味している。

つまり、ある自然数の区間内にある素数の個数の「２倍」の素数が出現するためには、自然数の範囲は「２倍」ではなく、「２倍より大きく」広がることになる。
これは、出現する素数の個数が減少することを意味している。

＜ガウスの素数定理＞
ガウスは「１からｘまで」の素数の出現率ｙを、ネイピア数を用いて「1/log(x)」と予測する。
すると、その区間の素数の個数：「π(x)」は「xy」で近似できることから次の式が成立する。→　π(x)～x/log(x)
これが「ガウスの素数定理」予想であり、１８９６年にプーサンとアダマールがそれぞれ独立に証明する。

＜素数相互の関係・・・双子素数＞
また、例えば、素数「３」と「５」にはどんな関係があるのだろうか。
この二つは「双子素数」と呼ばれ、隣同士の奇数がどちらも素数である。「５」と「７」も双子素数である。
このような双子素数は無限に存在するだろうと予想されているが、まだ証明はされていない。
なお、発見されている双子素数は「3,5」を除いて、「6n−1, 6n+1」という形になっている。「n=1」の時が「5,7」である。

＜平方剰余で関係を探る＞
ところで、次のような合同式「x＾2≡1 (mod 5)」には「x=1,4」という２個の解が存在する。解が存在する時は「平方剰余」であると言い、
「（1/5）＝（+1）」とルジャンドル記号で表す。
しかし、合同式「x＾2≡3 (mod 5)」に解は存在しない。その時は平方非剰余と言い、「（3/5）＝（−1）」と表す。

さて、合同式「x＾2≡5 (mod 3)」に解は存在するのか？

この合同式は「x＾2≡2 (mod 3)」と同じであり、解は存在しない。したがって、(5/3)＝(−1)である。

そうすると、（3/5）(5/3)＝(−1)(−1)＝(+1)であり、（3/5）か(5/3)のどちらかが分かれば他方も明らかになる。
そのためには（3/5）(5/3)＝(+1)であることを最初に知る必要がある。
そのための法則が、次の「相互法則」と二つの「補充法則」である。ただし、二つの素数ｐとｑは互いに素である。

＜下が「補充法則」である＞

いま「p=3」、「q=5」とすると、「p2-1=8」だから、
（2/3）＝ (5/3) ＝（-1）
また、「p-1=2, q-1=4」だから（3/5）(5/3)＝（+1）
したがって、（3/5）も(-1)であることが分かり、合同式「x2≡3 (mod 5)」には解が存在しないことが分かる。

この「平方剰余の相互法則」は、オイラーが予想し、１７９６年にガウスが証明する。

＜複素平面を提唱＞
ところで、二次関数を解くと複素数が解になることがある。その複素数の意味について考える数学者はまだいなかった時代である。
ガウスは１８１１年に「複素平面」を提唱し、複素数を数としてその存在意義を認めた。そして、実数の世界より広い複素数の世界で関数論や数論を展開したのである。

＜ガウス整数論＞
その一つが、後に「類体論」と呼ばれる領域に続く「ガウス整数論」である。ａ、ｂは有理数の一部である「有理整数」として、「a+bi」で表される数を「複素整数（ガウス整数）」と呼んで研究を進めた。

ガウス整数の集合を「i＝√(-1)」を用いてZ[i]と表すと、ガウス整数の世界は有理整数の集合Ｚより広く、拡張された世界であることが分かる。

そこで、ガウスは有理整数の世界の有理素数は、ガウス整数の世界でも「素元（素数）」と言えるのか？と探究を進める。

その時に用いたのは、フェルマーが提起し、オイラーが証明した「フェルマーの二平方定理」である。
それは、有理素数を「２」、「4k+1」、「4k+3」に分類することから始まる。

ガウスが辿り着いた結果は、「4k+3」型の有理素数は、拡張されたガウス整数の世界でも「素元（素数）」になることであり、ガウスはこれを「惰性する」と呼んでいる。

＜フェルマーの二平方和の定理＞
それに対して、「２」と「4k+1」型の有理素数は、拡張されたガウス整数の世界では「分解（分岐・完全分解）する」ことが明らかになる。

具体的には、「２」は「分岐」し、「５」は「完全分解」する。
2＝1+1＝12+12＝（1+i）（1−i）・・・＝(1+i)＾2
5＝1+4＝12+22＝（1+2i）（1−2i）

この「分解」で用いられているのが「フェルマーの二平方定理」である。「4k+1」型の有理素数は二つの整数の２乗の和にできるので「完全分解」となるのである。

なお、ガウス整数の世界では「１」の約数を「単数」と呼び、単数を掛けて同じになるものは同値となる。（なお、単数は±1, ±i, の４個）
したがって、（1−i）に単数の「i」を掛けると（i+1）となるので
「２」はガウス整数の世界では「（1+i）＾2」と「分岐」することになる。

＜類体論に続く＞
このようなガウスが始めた整数論は、百年後には日本の数学者：高木貞治（１８７５～１９６０）によって「類体論」という領域に成長し、いまなお世界中で研究が進められているという。

＜個人的な憧れ＞
この文の最後に、個人的な「整数論への憧れ」を記しておく。
筆者の曾祖父が、和算の流れをくむ規矩術を用いる大工であったことや、高木貞治と同じ１８７５年に生まれたことが遠因である。
そして、なにより、素数が出現するタイミングに「素数の不思議」を感じていることが「整数論」に憧れる源である。

そして、いま決意を新たにしていることは、高木貞治の「類体論」を少しでも理解したいということである。
道標は、数十年前に買い求めた高木貞治著の「初等整数論講義　第２版」である。