
コラッツ予想の分析
自然数において、偶数は「2で割り」、奇数は「3倍して1を加える」という作業を続けると「すべての自然数は1に至る」というのがコラッツ(1910~1990)の予想である。
例えば、「5」は奇数だから「3倍して1を加える」と偶数になる。それを2で割ると「8」である。「8」は偶数だから「2で割る」と「4」になり、・・・と続けると次のように「5回のステップ」で「1」に辿り着く。
5 → 16 → 8 → 4 → 2 → 1
途中の最大値は「16」になるが、この例を見るまでもなく、「2で割る」ことは自然数を小さくする作業であり、「3倍して1を加える」ことは、「3倍」に大きくはなるが、奇数を偶数に変えて小さくする準備作業であることが分かる。

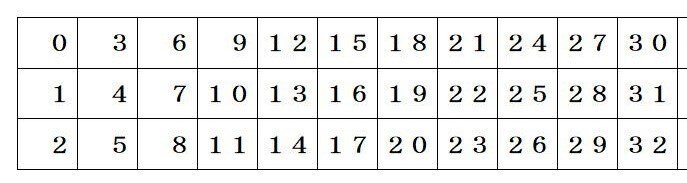
この表は「1から16まで」の自然数が「1」に辿り着くまでのステップ数と、途中の最大数である。(演習として確認してみて欲しい。)
自然数「5」のステップを樹状図に示すと次のようになる。

イメージとしては「2^n」が主となる幹で、その主幹から枝分かれして「5×2^m」という幹が伸びている。
自然数全体を樹状図に配置することを想像すると、次のようにまるで巨樹のようになる。

幹からは次々に枝分かれして、横に広がる。そして、主幹はもちろんであるが、すべての幹が限り
なく上に伸びて、梢が見えないほどである。ところが、「3」の因数を含む奇数k(=3m)で枝分かれした幹は、上に伸びるばかりで、その幹からは枝分かれしない。理由は明らかで、枝分かれする奇数kが存在すると仮定すると、「3k+1=9m+1=3×2^n=偶数」となり、矛盾。
つまり、主幹から枝分かれする奇数kの「2^m」倍から成る幹の「1/3」は枝分かれしないで上に伸びるばかりなのである。そのような幹にある自然数は、「1」に辿り着くステップ数が比較的小さいと考えられる。
例えば、自然数「1536」の「1」に辿り着くステップ数は「16」である。
この「16」は次のように計算できる。
すなわち、「1536」を因数分解すると「3×2^9」であり、「3」のステップ数「7」と「2^9」のステップ数「9」の合計を求めるのである。
さて、「1536」のステップ数は「16」であるが、近隣の数である「1535」、「1534」、「1531」のステップ数は「60」である。ちなみに、「1535」を因数分解すると「5×307」であり、素数「5」のステップ数「5」、素数「307」のステップ数「37」の合計は「1535」のステップ数にはならない。二つのステップ数の合計より少ない。
これは、「5」のステップ経路と、「307」の経路が継続していないことを意味し、ましてや「1535」の経路とは別経路であることを意味する。
簡単な例で示すと「15=3×5」の場合には、「3」、「5」、「15」のそれぞれのステップ数は「7」、「5」、「17」であり、「15」のステップ数は二つのステップ数の合計より大きい。
すなわち、ステップ数を計算で求めることは難しいのである。
また、不思議なことがある。主幹から枝分かれした幹から、さらに枝分かれして新しい幹になる。これは限りなく続くように思われる。すると、「1」に辿り着くステップ数には限りがないように想像される。ところが、「1から10^8まで」の自然数について、そのステップ数を調べてみると「500」を超えることは稀だという。不思議なことである。
素数「9887」のステップ数は「241」である。また、合成数「343711=47×71×103」のステップ数は「303」である。
ステップ数が「300」を超える自然数を探索すると、想像以上に難しい。
例えば、素数「10299683」のステップ数は「326」である。また、合成数「5555555555」のステップ数は「348」である。さらに、合成数「25000000000(250億)」のステップ数は「345」である。
ステップ数の大きい素数同士を掛けてもステップ数は減ることが多い。例えば、「10299683×3=30899049」のステップ数は「175」である。
ステップ数が「400」を超える自然数を、「勘だけで」見つけたのは最近である。(2023年9月21日の私の小さな発見である。)
その自然数は「5」を十九個並べた「555京5555兆5555億5555万5555」で、ステップ数は「471」である。
一位の数字を「5」から「7」、「9」に変えてもステップ数は変わらない。十の位を「7」に変えてもステップ数は変わらない。
それで、「555京」の部分を「575京」にしてみると、ステップ数は、驚くことに、「900」となったのである。
(「勘ではなく」プログラムを組めば簡単に求められるのであるが・・・)
ステップ数が「400」や「500」を超えることが稀であることは、コラッツ予想を解くヒントになると想像する。
さらに、コラッツ予想を解くための「分析」を進めることにする。
それで、「奇数なら3倍して1を加える」という作業を一般化して、「m倍して1を加える」ことにする。(mは奇数である。) 一般化する意味については、証明の方法が多様になる可能性があるからである。
たとえば、「m=1」の場合は、奇数を「3倍」しないので大きくならずに偶数に変えられるので、容易にコラッツの予想は証明できる。
「m=3」の場合がコラッツの予想である。
もしかしたら、「m=5」の場合は証明ができるかも知れないのである。最初の自然数が「3」であれば、「5倍して1を加える」と偶数になり、次のようなステップになる。
3 → 16 → 8 → 4 → 2 → 1
「m=5」の場合も「1」に辿り着けるように見える。
ところが、証明以前に、「m=5」の場合は「1」に辿り着けない事態が生じるのである。例えば、最初の自然数を「5」とすると、次のようなステップになる。
5 → 26 → 13 → 66 → 33 → 166 → 83 → 416 → 208 → 104 → 52 → 26 → →13 → 66 → ・・・
ステップは「13 → 66 → 33 → ・・・ → 104 → 52 → 26 → 13」と循環して、「1」には辿り着かない。
つまり、「m=1」でも「m=5」でもなく、「m=3」であるからこそ「1」に辿り着くというコラッツ予想の本質があると思われる。
ここで、大きく視点を変えてみることにする。これまでは、mを奇数として、「m=1、3、5、・・・」について試行してきた。奇数倍して1を加えることで「偶数」に変え、それを「2で割る」ことを繰り返してきた。これは、コラッツ予想を「偶数と奇数の世界」である剰余類「Z2={0,1}」の世界で扱ってきたことを意味する。

それで、「偶数と奇数の世界」ではなく、「mで割っていくつ余るか」という剰余類「Zm」の世界で考えてみることにする。 コラッツ予想を剰余類「Zm」の世界で考察したのは、東邦大学の白柳潔教授と学生の山中陽子さんである。
コラッツの予想は、自然数kが偶数なら「2」で割り、奇数なら「3倍して1を加える」という操作を繰り返すものである。これを次のように解釈するのである。
3k+1=(2+1)k+{2−1}=(2+1)k+{2−(k mod 2)}
これに従がえば「m=5」とすると、「Z5={0, 1, 2, 3, 4}」であるから、自然数を五種に分類することになる。
そして、「2の倍数である偶数なら2で割る」という作業を「5の倍数なら5で割る」とするのである。

kが「5の倍数」でない場合は、余りが「1、2、3、4」のいずれかになり、5の倍数にスルためには「4、3、2、1」を加えなければならない。つまり、「m=5」、「k=3」とすると、「3」は「5」で割れずに「余り3」であるから、(5+1)×3+{5−(3 mod 5}=18+2=20と計算する。
「20」は「m=5」で割れるから「4」で、「4」は「5」で割れないから(5+1)×4+{5−(4 mod 5)}=24+1=25
「25」は「5」で割れるから割ると「5」となり、さらに「5」で割ると「1」になる。
3 → 20 → 4 → 25 → 5 → 1
これで「一般化」に成功?したように見える。 それで、次に「m=3」、「k=5」としてみる。3で割った余りは「0」か「1」か「2」である。
「k=5」とすると余りは「2」である。従がって、「5」のステップは次のようになる。
→ (3+1)×5 +{3−(5 mod 3)}=20 + 1=21
そして、「21」は「3」で割れるから「7」になる。 これを続けると「1」へのステップは次のようになる。
5 → 21 → 7 → 29 → 39 → 13 → 18 → 6 → 2 →→ 9 → 3 → 1
この場合も「1」に辿り着き、一般化は成功したように見える。
ところが、「m=3」、「k=7」では「1」に辿り着けないのである。(ステップを示すと次のようになる。)
7 → 30 → 10 → 42 → 14 → 57 → 19 → 78 → 26→ 105 → 35 → 141 → 47 → 189 → 63 → 21 → 7
どうやら一般化は容易ではないようである。 それで、さらに視点を広げることにする。 コラッツ予想の原形に戻ると、全ての自然数は「1」に辿り着くことになる。そこで、この「1」は奇数ではないのか?と考えて「つづき」を試みる。
1 → 4 → 2 → 1
つまり、「1, 4, 2」は繰り返すことになり、一つの閉じたサイクルになる。そのサイクルの中の最小値が「1」である。 そう考えると、「m=5」「k=5」の場合のステップ「5 → 26 → 13 → 66 → 33 → 166 → 83 → 416 → 208 → 104 → 52 → 26 → 13 → 」は「1」には辿り着けないけれども・・・・・「 13 → 66 → 33 → 166 → 83 → 416 → 208 → 104 → 52 → 26 → 13」というサイクルが明らかになり、その最小値が「13」であることが分かる。
また、Z3における、「m=3」、「k=7」の場合も、ステップ「7 → 30 → 10 → 42 → 14 → 57 → 19 → 78 → 26 → 105 → 35 → 141 → 47 → 189 → 63 → 21 → 7」は、そのまま一つのサイクルになり、その最小値が「7」ということになる。
ここまで視点を広げることの意味は、証明するための「分析」である。コラッツ予想に含まれている不思議の分析であり、それを通して、自然数の奥深さに迫ることになる。 前に述べた「巨樹としての自然数」も同様である。偶数は「2で割る」ことを続けると「奇数」に辿り着く。したがって、コラッツ予想は、「全ての奇数は巨樹のどこかに配置されているはず」ということを示せば「証明」になるのである。
なお、コラッツ予想の原形は、与えられた自然数kが、偶数なら2で割り奇数なら「3倍して1を足す」、これを繰り返すと「1」に至る、という単純な構造をしている。 したがって、プログラムの学習にはよい教材になる。プログラム言語「python」で試作してみると、「1」に至る経路とステップ数が求められる。次のプログラムAがその例であり、この論文を書く上でも活用している。
<プログラムA>
def コラッツ(n):
if n % 2 == 0:
return int(n /2)
elif n % 2 == 1:
return int(3 * n + 1)
while True:
try:
print('計算する値を入力してください')
print('n=')
n = int(input())
m = 0
break
except ValueError:
print('---ERROR---整数を入力してください')
while コラッツ(n) !=0:
コラッツ(n)
n = コラッツ(n)
m = m + 1
print(int(n))
if n == 1:
print(str(m) + '回計算したら1になりました')
break
また、この<プログラムA>を用いて探索を続けていた時に、次のような結果を得て驚いてしまった。ステップ数や途中の最大数には「特異な数」があるのだろうか?などと論理的にはあり得ない妄想を抱いてしまったのである。
そして、その妄想から解放されるのに恥ずかしながら三日を要したのである。

上の表を見ると偶然とは思えない。大きさが近い数字であれば「1」に至る途中の最大数が同じ値になることは想像できる。しかし、「27」と「73」と「521」は相当に離れている。
それなのに、ステップ数も近い値で、最大数はピッタリ同じなのである。こんなことはあり得るのだろうか。
なお、「9232」は「24×577」である。
それぞれの自然数が「1」に至る経路を予想することは容易ではない。「129」、「521」、523」の「1」に至る経路を調べてみると最大数がピッタリ同じになることにナンノ不思議もないことが分かる。(次の経路略図を参照)

この記事が気に入ったらサポートをしてみませんか?
