
数学の力で、新しいイージング関数を作ってみた
こんにちは、ChocolaMintです。今回はイージング関数と数学の話です。

はじめに
「イージング関数」とは、何かの「変化率」を指定する関数のことです。ゲームでよく使われてる関数の一種なんです。詳しい紹介はこちらのサイトを参考してください。
何で新しいイージング関数を作るの?
少なくともゲーム業界では、大体「easeInQuad」など有名なイージング関数しか使いません。確かに多くの場合はチートシートからいい感じの関数を選べばいいんですが、特定の関数しか選べない時点で微調整は難しくなるのも当然ですね。
例えば、easeInQuadより遅い、easeInCubicより速い関数を選びたいとき、どうすればいいでしょうか。10個のミサイルを順番通りに加速度を段々上げたい(easeOut)とき、そもそもチートシートから選べるイージング関数の種類は7つしかないから、やっぱり無理でしょうか。
でも、実はパラメーターを増やせば、イージング関数だって微調整できるように作れるんです。興味のある方はぜひ続きを見てください。
セットアップ
今回はdesmosという無料アプリを使って、いろんなイージング関数を可視化させながら調整します。
イージング関数を作る前に、まずはイージング関数をちゃんと定義しないといけませんよね。ここでは以下の定義を使います:
パラメーター:
x:実数、範囲は0~1
p:実数、調整用のパラメーター、範囲はあとで別々に定義する
戻り値:実数、範囲は0~1
では、始めましょうか。
easeInを作ってみよう
easeInの形は大体こんな感じでしょう:

「指数」をパラメーターに入れ替われば、もっと細かい調整ができるようになります。(p>1)

もう一つの作り方は、「二つのイージング関数の補間」です。シンプルな線形補間で十分です。(0≦p≦1)

形さえ守れば、ちょっとアレンジしてもいいです。例えばさっきの関数の指数部分をこう変えても全然ありなんです:

easeOutを作ってみよう
さっき使った指数関数は実はeaseOutに近い形にもなれるんです。(0<p≦1)

でも、この関数は実はまだイージング関数として使えないんです。なぜかと言うと、こちらに注目してください:

この関数は、xが1の時、実は「速度が0になっていない」からです!
ここの「速度」(又は「変化率」)は、この関数の1回導関数のことです。
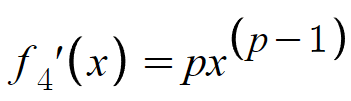
さっき作ったeaseIn関数たちは、実は皆「x=0の時、1回導関数の値が0になる」という条件を満たしているんです。
じゃあ、どうすればいいでしょうか。
何かしらの方法で「x=0」の部分を「x=1」の部分に入れ替えられますかね…
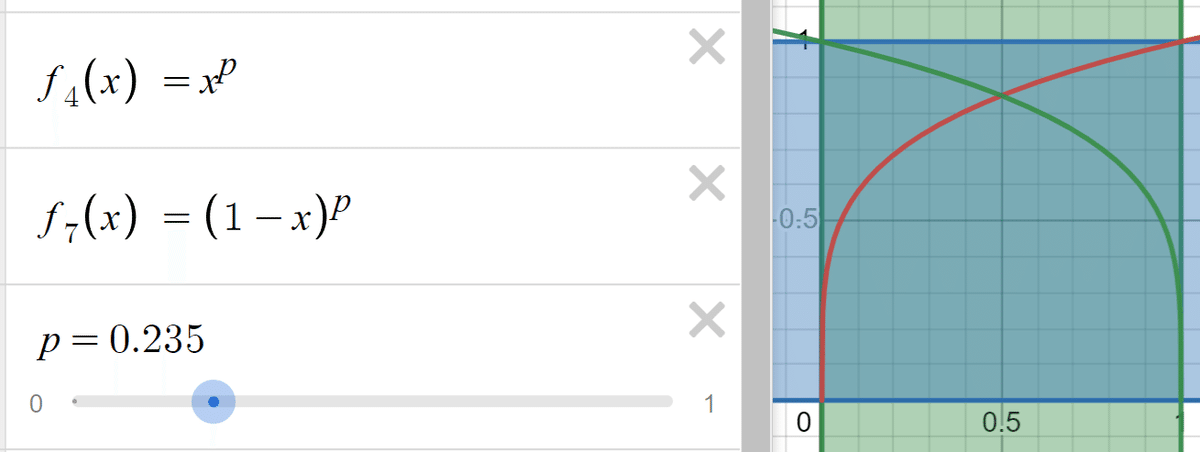



もちろん、easeInと同じく、ここでも線形補間からeaseOutが作れるんです:

easeIn/Outを作ってみよう
さっきの関数、惜しかったですね。調整する前はx=1の時の速度が0になれなかったけど、調整した後は逆にx=0の時の速度が0になれなくなりました。一つの関数で、パラメーターをいじってるだけでeaseInとeaseOutのどっちかにすぐに変えることができる、そんな関数は本当に存在するんですか?
例えば…こういう関数はどうでしょう?

形は一見あってるけど、本当に速度が0になってるかどうかは、数学で分析しないとわかりません。1回微分したら、このような導関数が導けます:

xを0に代入すると、こんな感じになります:
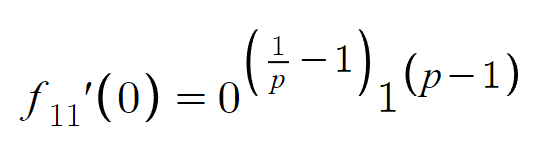
xを1に代入すると、こんな感じになります:
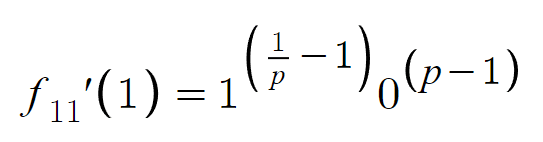
これで言い切れるんですね!このちょっと見た目が変な関数は、pの範囲により、easeInとeaseOut両方の属性を持つことができるんです。
easeInOutを作ってみよう
easeInOutも作ってみましょう!easeInOutって、「easeInからのeaseOut」のイメージがあります。こんな感じです:

今まで指数関数しか使っていないので、気分転換にコサインも入れてみましょう:


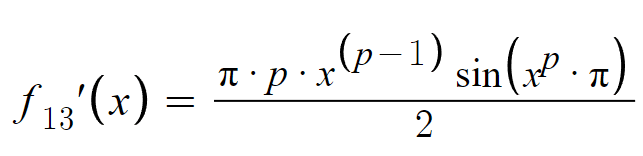
easeOutInを作ってみよう
もう一つのeaseInOutまたはeaseOutInの作り方は、二つのイージング関数を繋ぐことです。
例えばeaseInOutQuadは、二つの二次関数からできている関数です:


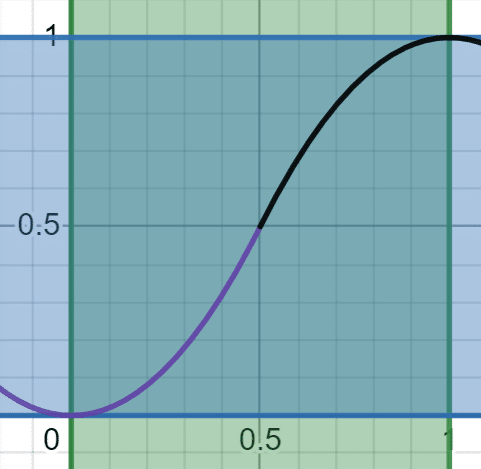
注意しなければならないところは、繋いで生み出した関数も連続で微分可能な関数じゃないとイージング関数として使えません。速度が途中に急に変わったらスムーズじゃなくなるからです。
さっき言ったように、easeOutの特性の一つは、x=1の時の1回導関数が0になります。そして、easeInのほうは逆にx=0の時の1回導関数が0になります。つまりこの二つのポイントから繋ぐと、連続で微分可能な関数になります。




easeInOut/OutInを作ってみよう
さっきはeaseOutからのeaseOutだったけど、順番が変わったらどうなるでしょうか。試してみましょう!

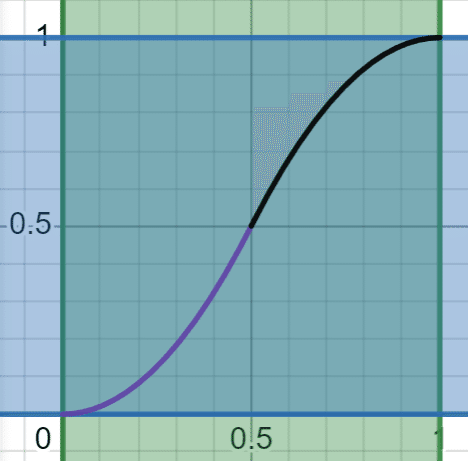

…が、ここでx=0.5の時の可微分性を証明するとちょっとややこしくなるので、細かい証明はここで割愛します(確かこれは大学の微分積分学の範囲なので、興味のある方はそちらの教科書を参考してください)。
最後に
いかがでしょうか。意外と知ってる数式を組み合わせてるだけで色んなイージング関数が作れるんですね。数学の知識もちゃんと応用できて、素晴らしいことだと思います。
今回は指数とコサインしか使わなかったけど、今まで学校で学んだ関数は全部イージング関数に使えるんです。例えばこういう化け物イージング関数も全然ありなんです:

ただ、ゲームに入れる時は、パフォーマンスの配慮もしなければなりません。イージング関数を使ってるオブジェクトが多くなったら(例えば弾幕シューティングに使ってる時)、なるべく軽い関数を選んだほうがいいと思います。ベンチマーキングしてもいいと思います。
あと、イージング関数の種類はeaseIn、easeOut、easeInOut、easeOutIn以外にもあります(easeInBackとか)。いつかそういう特殊なイージング関数の微調整できるバージョンも作ってみたいですね。
たまに暇つぶしにイージング関数を作ってみませんか?ご覧いただきありがとうございました。
あとがき
今回の数学の証明はそこまで厳密ではありません。特に関数の値域と連続性そのあたりの説明は省略しました。良い子のみんな、大学の授業ではああいう雑な証明を書いてはいけませんよ!
この記事が気に入ったらサポートをしてみませんか?
