離散時間信号と離散時間フーリエ変換、離散フーリエ変換
離散時間信号とは
離散時間信号とは、元の連続信号から一定時間ごとに値を取り出した信号である。そのため飛び飛びの時刻にしか値を持たない。
そして、連続信号から一定時間ごとに値を取り出し、離散時間信号を作ることサンプリングという。
サンプリングする時の時間間隔のことを、サンプリング周期といいT_sとかく。また、T_sの逆数がサンプリング周波数でありf_sとかく。サンプリング角周波数は2π/T_sでありΩ_sとかく。
そして注意したいのが、連続時間信号の横軸の単位はtだったが、離散時間信号の横軸の単位はnであり、正規化時間という。
正規化時間には単位はなく、1サンプル、2サンプルと数えるのがいいだろう。
離散時間信号になって横軸の単位が正規化時間に変わったので、今まで周波数や角周波数と呼んでいたものも変わる。
離散時間信号では周波数を「正規化された周波数」。角周波数を正規化角周波数とよぶ。
正規化された周波数は、1サンプル時間に何回振動するかを表し、正規化角周波数は、1サンプル時間に何rad位相が進むかを表しωとかく。そしてこの定義より、ω = ΩT_sの関係がある(Ωは普通の角周波数)。なのでT_sが1の時、角周波数と正規化角周波数は一致する。
ただし、離散時間信号では、ことわりがない限り、正規化角周波数のことを単に角周波数というので注意が必要だ。
離散時間フーリエ変換
離散時間信号をそのままフーリエ変換したらどうなるか考えてみよう。
対象とするサンプリング周期が1の離散時間信号をf[n]として、これを連続信号とみなしてフーリエ変換してみる。
f(t)はt = nの時f[n]で、それ以外では0。
よってフーリエ変換の積分の中身のf(t)e^(jωt)はtがn以外では0であり、t = nの時も面積がないので積分しても0になる。
つまり、離散時間信号を連続信号とみなしてフーリエ変換しても0になり意味がない。
これを解消させるために、t = n以外のところで値を持たせることにする。つまり、t =n-1/2とt=n+1/2の間はt=nの時の値f[n]e^(jωt)と等しいと考える。
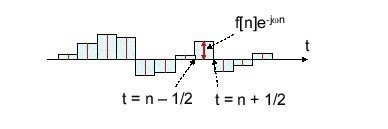
こうすることで、短冊それぞれの面積の総和を計算すれば良くなる。短冊の横幅は1なので
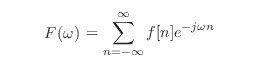
となる。これが離散時間フーリエ変換である。
この離散時間信号の周波数領域での周期を考えてみる。サンプリング周期が1なので時間領域で1ごとに値を持つ離散時間信号である。
つまり、ω = Ω = 2π/Ts = 2π。よって周波数領域での周期は2πであることがわかる。以上から離散時間信号の周波数スペクトルは常に周期的で、周期は2π。またωは連続変数なので周波数スペクトルは連続である。
離散時間フーリエ逆変換
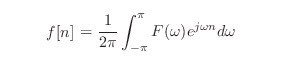
F(ω)は周期2πで連続なので積分となり、積分範囲は通常-π~πまでになる。
離散フーリエ変換
さて、これまでの話で出てきた離散時間フーリエ変換には、一点困るところがある。それは、離散時間フーリエ逆変換がコンピュータの中では計算できないからである。
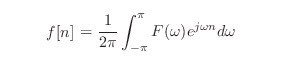
離散時間フーリエ逆変換の式を見ると、連続変数ωが入っておりコンピュータで厳密に計算できない。
ではどうすれば良いのか??
答えは、周波数領域も離散化することである。
以下は離散フーリエ変換と逆変換の式である。
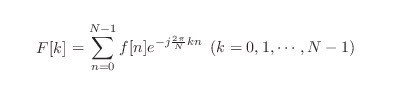
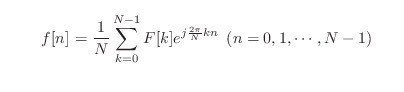
よくみるとF[k]が離散的になっていることがわかる。kは周波数のインデックスを表す整数であり、F[k]はf[n]に含まれる正規化周波数2πk/Nの振幅と位相を表す。
kが大きくなっても周波数が高くなるわけではないことに注意が必要で、また周波数スペクトルは周期的なのでk = でk=0に戻る。
