フーリエ級数展開、フーリエ変換のイメージ

大学でフーリエ級数展開、フーリエ変換について学んだが、なんとなく式を覚えてテストに臨み、本質的な理解ができていないと思ったので、改めて学び、イメージを下記に書き記す。

フーリエ級数展開とは？

まず、フーリエ級数展開がしていることのイメージとして、

波を複数の波の和で表す

ということを頭に入れておいて欲しい。

そして、複数の波の和で表される元となる波として、周期的で連続な信号f(t)を考える。

f(t)のイメージとしては以下のような波だ。

複雑な波形をしているが、これは複数の波が足し合わされてこの形になっている。ではどのような波が足し合わされているだろうか？？

早速だが、フーリエ級数展開の式は以下のように定義される

左辺は、先ほど示した波であり、右辺は複雑だがよく見ると、cosとsinが足し合わされていることがわかる。つまり、上図の波がどのような波の足しあわせで作られているかを示している。

右辺について詳しくみてく。

a_0は定数であり波の直流成分を表す。つまり、周波数0の振動していない成分である。また、cosとsinは振動成分を表している。そしてこれはkによってどのような振動が変わる。(kは自然数)

例えばk=1の時、角周波数は2π/T_0であり、これは時間がT_0経過したら波の位相が2πすすむことを示している(ちなみにk=1の時の角周波数を基本角周波数とよぶ)。k=2の時、角周波数は4π/T_0であり、時間がT_0経過したら位相が4πすすむことを示す。

つまり、kが大きい数ほど、早く振動している波、ということになる。

最後に、a_k、b_kはそれぞれcosとsinの振幅を表しており、フーリエ係数と呼ばれている。

このnoteではイメージについてまとめたいため、フーリエ係数の求め方については省略する。

ここまでをまとめると、連続な周期関数f(t)は三角関数の無限和で表すことができ、足し合わされる三角関数の角周波数は、基本角周波数のk倍である。

ここまで理解できたなら、以下のよく出てくる図についても理解できると思う。

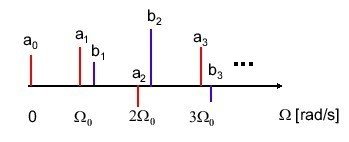
元の周期信号(波)が、基本角周波数Ω_0の整数倍の周波数を持つ成分に分解され、a_k、b_kでそれぞれの成分がどのくらいか示されている。

このような図を周波数スペクトルという。

三角関数型と複素指数関数型

さて、これまでみてきたのは三角関数型のフーリエ級数展開だが、フーリエ級数展開には複素指数関数型のものもある。

複素指数関数型のフーリエ級数展開は三角関数型のフーリエ級数展開の式にオイラーの公式を使って変形することで導出できる。

最後の行への変形だが、Σの中の第一項のe^(j2πkt/T_0)はk=1~∞の足しあわせであり、第二項目のe^(-j2πkt/T_0)はk=-1~-∞の足しあわせである。またa_0はk=0の項と考えることができ、それらをまとめてF_k*e^(j2πkt/T_0)としている。

またF_kはフーリエ係数であり、振幅と位相を表す。三角関数型なら振幅のみであったが、今回はF_kが複素数になる場合もあるからだ.

この式のイメージを考えていく。そのためにはe^(j2πkt/T_0)のイメージを持つことが大事である。

e^(j2πkt/T_0)は単位円上を反時計回りにすすむ螺旋のイメージだ。「単位円上で螺旋が何周するか」が周波数であり、「単位円上で螺旋の位相が何rad進むか」が角周波数である。つまりkが増えるほど、早く振動する螺旋ということになる。

これらのイメージから、複素指数関数型のフーリエ級数展開の式は、f(t)を、kが異なる多くの螺旋の足しあわせで表そうとしているものと言える。

複素指数関数型のフーリエ級数展開のスペクトルを見てみる。

元の周期信号(波)が、基本周波数の整数倍の周波数を持つ成分に分解され、各角周波数について正と負の組がある。またF_kは複素数のなので絶対値と偏角を持つ。

上の図を「振幅スペクトル」、下の図を「位相スペクトル」という。

フーリエ変換

先ほどまでは周期的な波を考えていたが、これが非周期的であった場合どうすれば良いか？？

この時に出てくるのがフーリエ変換である。

周期的な波→非周期的な波になった場合

フーリエ級数展開のスペクトルをもう一度見てみる。

三角関数型、複素指数関数型のスペクトルどちらもスペクトルが飛び飛びである。

スペクトルの間隔は、元の波の周期がT_0だったので、Ω_0 = 2π/T_0である。

そして、この周期T_0をどんどん伸ばしていってみる。スペクトルの間隔が2π/T_0だったので、T_0が大きくなるほど間隔が狭くなることがわかる。

そして周期的でない波は、周期∞の波と考えることができる。

つまり、非周期の波のスペクトルは、飛び飛び(離散的)ではなく連続になる。

フーリエ変換とフーリエ逆変換の式

上がフーリエ変換、下がフーリエ逆変換の式である。

フーリエ変換の右式には、時間変数tと角周波数変数Ωが含まれているが、tで積分するのでΩが残る。つまり、「連続時間上の関数から、連続角周波数上の関数への変換」を表している。

フーリエ逆変換の右式も同様に、tとΩが含まれているが、Ωで積分をしているのでtが残る。つまり、「連続角周波数上の関数から、連続時間関数への変換」を表している。

また、Ωは角周波数を表す連続信号であり、F(Ω)はf(t)に含まれる角周波数Ω成分の振幅と位相を表している。

もう一度フーリエ逆変換の式を見ると、波f(t)はF(Ω)e^(jΩt)の足しあわせ（積分)で表されている。

つまり、フーリエ級数展開の意味に対応しているのはフーリエ逆変換の方である。

一方、フーリエ変換は、フーリエ係数を求める計算に対応している。