今日の最大・最小 240208

最大値、最小値を求めよ、とりうる値の範囲を求めよ、という問題は多いです。関数関係が見つかった、関係式が見つかったときに、range を調べたくなる感覚は数学のよさの一つだと思います。

a, b を正の数とします。さらに、$${a+2b\leqq 2}$$ かつ $${a^2+b^2\leqq 1}$$ を満たす a, b に対して、$${3a+2b}$$の最大値を調べてみましょう。

ここに限らず私は解き方や答えを教えるよりも、もう少し上の次元、問題をどう見るかということを伝えたいと思っています。例えば、この問題の解答であれば、どこかにありますし、解法を知っている人も多いでしょう。例題があって、その解法を覚えるという学習法は、世の中では見たことのない問題に対する解を見つけてほしいということが多いので、気を付けなければならないと思っています。

そもそもこの問題では、条件を満たすa, b をいろいろ代入してみたときの最大値は？ と問われています。上の注意と同じ事ですが、問題はこう考えなければならないという絶対はありません。
まず、a, b 両方動かすよりもどちらか一方にしてみようと思います。例えば、同じ a なら b を大きくすれば $${3a+2b}$$ (以下 k とおきます。)は大きくなります。 k は b に関して単調に増加します。したがって、k が最大になるのは、
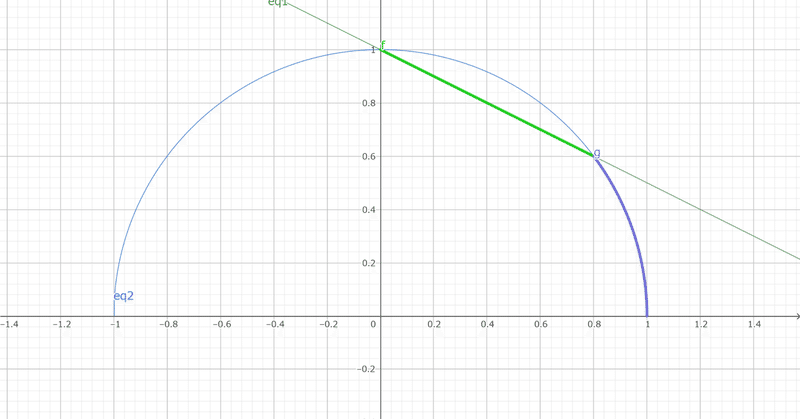
$${0\lt a\leqq \frac{4}{5}}$$ のときは $${a+2b=2}$$ …①
$${\frac{4}{5}\leqq a\lt 1}$$ のときは $${a^2+b^2=1}$$ …②
この (a, b) に絞られます。

①について考えてみましょう。
$${3a+2b=k}$$, $${a+2b=2}$$ から b を消去すると、$${k=2a+2}$$
①の範囲では k はa に関して単調に増加して、$${2\lt k\leqq\frac{18}{5}}$$ ということが分かります。

②について考えてみましょう。
$${a^2+b^2=1}$$を満たすa, b (もう少し細かいですが)で、$${3a+2b=k}$$ のとりうる値の範囲を調べるのです。いろいろな方法があります。$${(a,b)=(\cos\theta,\sin\theta)}$$ と置く方法もあります。
ここでは k を $${\overrightarrow{\rm ON}=(3,2)}$$ と $${\overrightarrow{\rm OP}=(a,b)}$$ の内積とみてみましょう。角NOP を θ と置きます。(a, b) は ②の条件を満たすとします。
$${k=\overrightarrow{\rm ON}\cdot\overrightarrow{\rm OP}}$$ $${=\sqrt{13}\cos\theta}$$
この式の値は θ = 0 で最大となりますが、②で θ = 0 となる (a, b) はとれるでしょうか？

とれます、というのが答えです。
$${a+2b=2}$$, $${a^2+b^2=1}$$ を同時に満たすA$${(\frac{4}{5},\frac{3}{5})}$$ を考えます。
直線OA の傾きは $${\frac{3}{4}}$$, 直線ON の傾きは$${\frac{2}{3}}$$ だからです。
そして最大を与える(a, b) は
$${\sqrt{13}=\dfrac{3\cdot 3+2\cdot 2}{\sqrt{13}}}$$ ですから、$${(a,b)=\left(\dfrac{3}{\sqrt{13}},\dfrac{2}{\sqrt{13}}\right)}$$
②の範囲では $${3\lt k\leqq\sqrt{13}}$$ であることがわかります。

以上より、$${3a+2b}$$ は $${(a,b)=\left(\dfrac{3}{\sqrt{13}},\dfrac{2}{\sqrt{13}}\right)}$$ で最大値$${\sqrt{13}}$$ をとります。

図を描いたり、図で説明することは大切なことですが、完ぺきな図というものは困難ので、考え方を説明するときには　図より　というのは出来るだけ避けるようにしたいと思っています。