LaTeXの勉強2(例題あり) 「三角関数」 でよく使う数式の表現

前置き

こんにちは。昨日に引き続き、LaTeXの勉強をしていきましょう。今回は、三角関数の分野でよく使う数式をNotionを用いて表現していきます。

sin,cos,tan

\text{sin}\alpha,\text{cos}\alpha,\text{tan}\alpha

LaTeXでは、文字を入力したとき斜体になるので、\textまたは\mathrmで直立体の文字に変更できます。

度数

90\degree

πとθ

\pi,\theta

角を表す記号「∠」

\angle ABC

≤,≥(小なりイコール、大なりイコール)

\leq,\geq

空白

A\space B

改行

A \\ B

問題集

今回のLaTexの数式表現は以上です。最後に問題が5問あるので、前回のコマンドも使って実際に手を動かして解いてみましょう！

問１　三角比の相互関係

※\text,\spaceは使っても使わなくても大丈夫です。

問１　解答

\text{tan}\alpha=\frac{\text{sin}\alpha}{\text{cos}}\space,
\text{cos}^2+\text{sin}^2\alpha=1\space,
1+\text{tan}^2\alpha=\frac{1}{\text{cos}^2\alpha}

問２　扇形の弧の長さと面積

※\text,\spaceは使っても使わなくても大丈夫です。

問２　解答

l=r\theta,\space S=\frac{1}{2}r^2\theta(=\frac{1}{2}rl)

問３　証明問題

※\text,\spaceは使っても使わなくても大丈夫です。

問３　解答

\frac{\text{sin}\theta}{1+\text{cos}\theta}+
\frac{1+\text{cos}\theta}{\text{sin}\theta}=
\frac{2}{\text{sin}\theta}

問４ 加法定理１

※\text,\spaceは使っても使わなくても大丈夫です。

問４　解答

\text{sin}(\alpha\pm\beta)=
\text{sin}\alpha\text{cos}\beta\pm
\text{cos}{\alpha}\text{sin}\beta

問５　加法定理２

※\text,\spaceは使っても使わなくても大丈夫です。

問５　解答
\pmで±、\mpで∓となります

\text{tan}(\alpha\pm\beta)=
\frac{\text{tan}\alpha\pm\text{tan}\beta}{1\mp\text{tan}\alpha\text{tan}\beta}

問６　２倍角の公式

問６　解答

\text{cos}\alpha=\text{cos}^2\alpha-\text{sin}^2\alpha\\
=2\text{cos}^2\alpha-1\\
=1-2\text{cos}^2\alpha

問７　半角の公式

問７　解答

\text{sin}^2\frac{\alpha}{2}=\frac{1-\text{cos}\alpha}{2}

問８　三角関数の合成

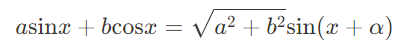
問８　解答

a\text{sin}x+b\text{cos}x=\sqrt{a^2+b^2}\text{sin}(x+\alpha)

今回は以上です。ご覧いただきありがとうございました。