小学生の算数で微分方程式を解く

この修正SIRモデルの微分方程式を解きましょう。「解く」というのは$${S}$$、 $${I}$$、$${R}$$、を時間$${t}$$の関数として表現することです。でも、数学的に解くのは小学生の算数では無理があるので、加減乗除だけで泥臭く計算することにします。

2020年10月22日の感染者$${I_{10/22}}$$は94,014人でした$${^{1)}}$$。10/23の感染者$${I_{10/23}}$$は9,4706人です$${^{2)}}$$。したがって、10/23の感染者の増加分$${ΔI_{10/23}}$$は692人となります。（Δはデルタと読みます。ここでは1日の増加分を示します）。この関係を式で書くと、

$${I_{10/23}=I_{10/22}+ΔI_{10/23}}$$

となります。$${n}$$日目の感染者$${I_n}$$はその前の日の感染者$${I_{n-1}}$$に$${n}$$日目の増加分をたせばよいのです。

$${I_n=I_{n-1}+ΔI_n}$$

これを漸化式といいます。0日目から順にやっていきましょう。人口$${S_0}$$人の集団があり、そこに$${I_0}$$人の感染者が入ってきたとします。0日目の感受性者は$${S_0}$$人、感染者は$${I_0}$$人、回復者は0人です。すると次の日の増加人数は、

$${ΔS_1=-kS_0I_0}$$

$${ΔR_1=I_0/T}$$

$${ΔI_1=kS_0I_0-I_0/T}$$

となります。累積人数$${S}$$、$${I}$$、$${R}$$は、

$${S_1=S_0+ΔS_1}$$

$${R_1=R_0+ΔR_1}$$

$${I_1=I_0+ΔI_1}$$

同様に2日目、3日目と計算して365回同じ操作をくり返せば1年間の変化が描けます。$${S}$$、$${I}$$、$${R}$$は増加分をたして積み上げていった値で、$${dS/dt}$$、$${dI/dt}$$、$${dR/dt}$$の積分となります。

実際に数字をエクセルに入れてみましょう。日本の人口1億2588万人全て感受性者だとすると、$${S_0=1.26}$$x$${10^8}$$（エクセルでは1.26e8と入力します）、$${R_0=0}$$。ここに感染者が1人空港検疫から漏れて入国したとします。感染してから発症するまでの潜伏期間が4日で感染力がなくなるのは発症後6日ということですから$${^{3)}}$$感染期間は10日としましょう。ということで、$${I_0=1}$$、$${T=10}$$とします。

「感染者1人が増やす新たな感染者の数」を「再生産数」(通常はRを使いますが、回復者RとまちがうのでここではQを使います)といいます。感染期間を$${T}$$とすると1日あたり$${Q/T}$$増やすことになります。1日の日本の新たな感染者の増加数$${-ΔS}$$はこれに現在の感染者数$${I}$$をかけたものになります。

$${-ΔS=kSI=IQ/T}$$、すなわち$${k=Q/(ST)}$$、$${Q=kST}$$

$${S}$$は時間の関数ですから、$${Q}$$は時間$${t}$$の変化とともに増減する変数で、$${Q_t}$$を「実効再生産数」と呼びます。特に、最初の日の再生産数$${Q_0}$$を「基本再生産数」といいます。とりあえず普通使われる2.5にしておきます。

$${k=Q_0/(S_0T)}$$

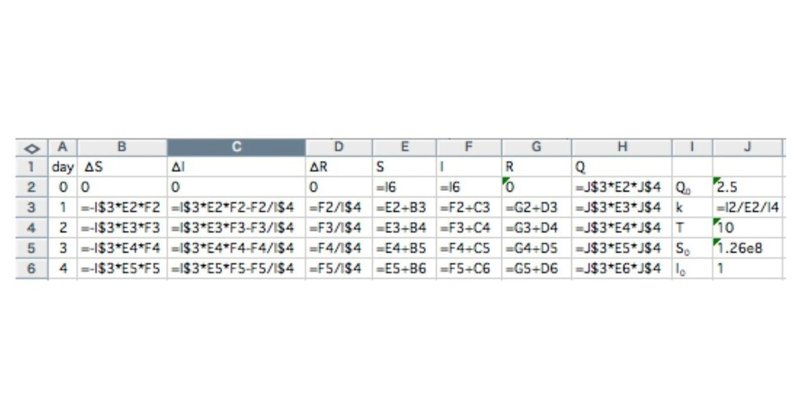
これらの数値を、エクセルのday0とday1の行に入力すると表1のようになります。Day2以降はday1のA-H列の入力をコピペします。このとき定数である$${k}$$と$${T}$$の値はコピペでずれないようにJ$3, J$4のように行を示す数の前に$を入れます。

$${^{1)}}$$https://www.mhlw.go.jp/stf/newpage_14377.html

$${^{2)}}$$https://www.mhlw.go.jp/stf/newpage_14412.html

$${^{3)}}$$JAMA Int Med 180, 1156 (2020)

表1. 修正SIRモデルのエクセルへの入力