【第6回垂れ流し数学模試】文型第4問 解答例
皆さんこんにちは。
今回は第6回垂れ流し数学模試の文型の第4問の解答例です。
直線$${y=ax+b}$$が放物線の一部と共有点をもつような$${a}$$, $${b}$$の存在領域を図示する問題でした。
問題
$${xy}$$座標平面上で, 曲線$${y=4-x^2}$$の$${-2\leqq x\leqq 2}$$の部分を$${C}$$とする.
$${a}$$, $${b}$$を実数とするとき, 直線$${y=ax+b}$$が$${C}$$と共有点をもつような$${a}$$, $${b}$$の存在範囲を, $${ab}$$平面上に図示せよ.
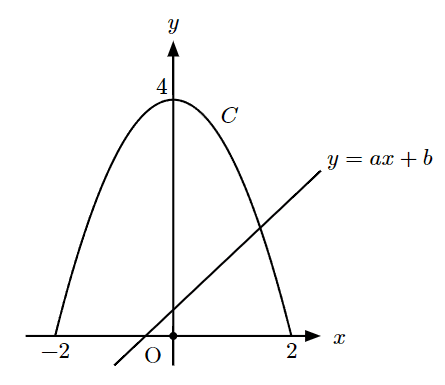
考え方
・直線$${y=ax+b}$$が$${C: y=4-x^2\quad (-2\leqq x\leqq 2)}$$と共有点をもつ
ということと,
・方程式$${ax+b=4-x^2}$$が$${-2\leqq x\leqq 2}$$の範囲の実数解をもつ
ということは, 互いに同値です.
したがって, 後者の考え方で行きましょう.
$${ax+b=4-x^2}$$を変形すると$${x^2+ax+b-4=0}$$となり, これは$${x}$$の2次方程式です.
さらに$${f(x)=x^2+ax+b-4}$$とおくと, $${f(x)}$$は2次関数なので,
グラフは$${y}$$軸に平行な直線を軸にもつ放物線ですね。
$${x^2+ax+b-4=0}$$が$${-2\leqq x\leqq 2}$$の範囲の実数解をもつとき,
$${y=f(x)}$$のグラフについて次の2パターンがあります.
(i) $${y=f(x)}$$のグラフの頂点の$${x}$$座標が-2以上2以下, $${y}$$座標が負,
かつ$${f(-2)\geqq 0}$$かつ$${f(2)\geqq 0}$$
(ii) $${f(-2)}$$と$${f(2)}$$の少なくとも一方が0, または互いに異符号.
つまり, $${f(-2)f(2)\leqq 0}$$
以上(i), (ii)のそれぞれの条件を$${a}$$, $${b}$$を使って表したうえで,
それらの表す$${ab}$$平面上の領域の少なくとも一方に入る部分が求める領域です.
解答例
問題の$${a}$$, $${b}$$の条件は,
・$${x}$$の方程式$${ax+b=4-x^2}$$が$${-2\leqq x\leqq 2}$$の範囲の実数解をもつ
ことと互いに同値である.
$${ax+b=4-x^2}$$を変形すると$${x^2+ax+b-4=0}$$となる.
$${f(x)=x^2+ax+b-4}$$とおくとき, $${y=f(x)}$$のグラフは$${y}$$軸に平行な直線を軸にもつ放物線で,
$${f(x)=\left(x+\dfrac{a}{2}\right)^2-\dfrac{a^2}{4}+b-4}$$から
放物線の頂点の座標は$${\left(-\dfrac{a}{2}, -\dfrac{a^2}{4}+b-4\right)}$$,
軸の方程式は$${x=-\dfrac{a}{2}}$$である.
方程式$${x^2+ax+b-4=0}$$が$${-2\leqq x\leqq 2}$$の範囲に実数解をもつような$${f(x)}$$の条件は,
次のいずれかを満たすことである.
(i) $${y=f(x)}$$のグラフの頂点の$${x}$$座標が-2以上2以下, $${y}$$座標が負,
かつ$${f(-2)\geqq 0}$$かつ$${f(2)\geqq 0}$$

(ii) $${f(-2)}$$と$${f(2)}$$の少なくとも一方が0, または互いに異符号.
つまり, $${f(-2)f(2)\leqq 0}$$

(i)の場合
$${a}$$, $${b}$$が以下をいずれも満たす.
・$${-2\leqq-\dfrac{a}{2}\leqq 2}$$より$${-4\leqq a\leqq 4}$$
・$${-\dfrac{a^2}{4}+b-4\leqq 0}$$より$${b\leqq \dfrac{a^2}{4}+4}$$
・$${f(-2)=4-2a+b-4=-2a+b\geqq 0}$$より$${b\geqq 2a}$$
・$${f(2)=4+2a+b-4=-2a+b\geqq 0}$$より$${b\geqq -2a}$$
(ii)の場合
$${a}$$, $${b}$$が$${f(-2)f(2)=(-2a+b)(2a+b)\leqq 0}$$をみたす.
この条件から,
$${\begin{cases} -2a+b\leqq 0\\ 2a+b\geqq 0\end{cases}}$$ または $${\begin{cases} -2a+b\geqq 0\\ 2a+b\leqq 0}\end{cases}$$
すなわち,
$${\begin{cases} b\leqq 2a\\ b\geqq -2a\end{cases}}$$ または $${\begin{cases} b\geqq 2a\\ b\leqq -2a\end{cases}}$$
以上を合わせて, 求める$${a}$$, $${b}$$の存在領域を$${ab}$$平面上に表すと, 以下の図のピンク色の部分になる. ただし, 境界部分はすべて含む.

まとめ
以上, 第6回垂れ流し数学模試の文型第4問の解答をお届けいたしました。
図形と方程式の分野ですが, 問題で課された条件自体は方程式の問題に容易に帰着できますので,
$${ab}$$平面の図示以外は実質2次方程式の解の条件の問題です.
そういうわけで, 難易度もそんなに高くないのではないかと思います。
方程式の解の条件の問題も, 図形がある条件を満たすような領域の図示も,
テーマとしては頻出なので, よく押さえておきましょう.
それではこの記事を終わりたいと思います。
ここまでお読みいただきありがとうございました。
サポートしていただけると励みになります! よろしくお願いいたします!
