
検定からのもう一歩。検出力とサンプルサイズを考える。
先日投稿したこの結果には差があるのか(統計的な検定についての考え方) に関しての続きの会です。
前回の範囲までは統計検定でいうとだいたい2級レベルです。ここからさらに一歩進むために理解するべきことが、検出力とそれに合わせてのサンプルサイズの考え方です。
このあたりを理解するために4つのステップで考えていきたいと思います。
①第1種の過誤と第2種の過誤について理解をしたうえで、
②検出力とは何か、
③検出力は何によって決まるのか、最後に、
④適切なサンプルサイズはどれくらいか
という流れで行きたいと思います。
第1種の過誤と第2種の過誤について
きいたこともあるかもしれませんが、ベースの考え方として大事な概念です。第1種の過誤(ファーストエラーとかアルファエラーともいったりするはず。)は、本来、帰無仮説が真でなので、検定では棄却できない結果になってほしいはずなのに棄却域の結果が出てしてしまうことで、この確率が帰無仮説の優位水準となります。通常外側の5%とかになるので、ほぼないよねってことなんですが、5%の確率でそういうことが起こってしまうわけです。前回にも書きましたが、ここが検定としてのあきらめの水準になるわけです。
第2種の過誤は、逆に本来、対立仮説を取るべきだったところ、今回の結果では採用できない確率になります。いいかえると、帰無仮説が棄却できず、対立仮説を取ることができない確率です。
この第2種の過誤にならない確率のことを検出力と呼ぶのです。
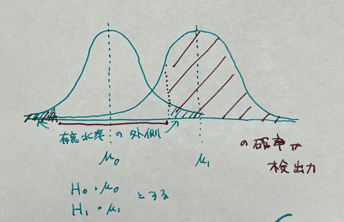
ちなみに両側検定の場合、上の図のように両サイドに優位水準があります。左端のところは検出力にカウントすべきところがあることは覚えておいた方が良いらしいです。実質限りなくゼロに近くなるので無視するのですが、そこを抑えたうえで無視すべきと。
検出力とは何か?
検出力とは何かというと、今回の結果の対立仮説を採用できる確率になります。前回のグミの好みの例をもう一回利用して確認してみましょう。
具体的なイメージをつかむために、今、食べているもも味のグミと明日用のマスカット味のグミの好きな割合を比較してみます。ランダムに集まった100人ずつどちらかを食べてもらい、スキか嫌いかを判定してもらったという例を考えてみましょう。
私の個人的な意図が多分に入った仮の回答結果として、
・もも味は100人中 85人が好きと回答(スキ率85%)
・マスカット味は100人中 75人が好きと回答(スキ率75%)
となったとします。
帰無仮説:桃とマスカットのスキ率は同じ(85%である)
対立仮説:もも味よりもマスカット味のスキ率は低い(75%である)
となります。
前回の結果から
もも味はスキ率85%を頂点(平均)と、3.57%の標準偏差の正規分布と考えます。
今回優位水準を片側(下の方に)5%として考えてみましょう
標準正規分布で両側5%の優位水準となるスコア(Z得点とかいいますね)は1.96です。(試験でよく出る数字です。大体みんな暗記している数字だと思います。頭で概算するときはざっくり2倍と覚えててもいいかなと思っています。標準正規分布:平均0、標準偏差1の正規分布の時、1.96以上離れるとそれぞれ両サイド2.5%以下の確率になるということです。
85% - 3.57%*1.96 =78.06以下だと5%以下の確率でしか起きないということになり、今回の75%は低過ぎるよねというはなしになります。では、このとき、75%の結果が出た場合、どれくらいの確率で第2種の過誤が起きるか、その反対の確立である検出力を考えてみます。(わかりやすくこの二つのグループのばらつきは同じと考えちゃいます)
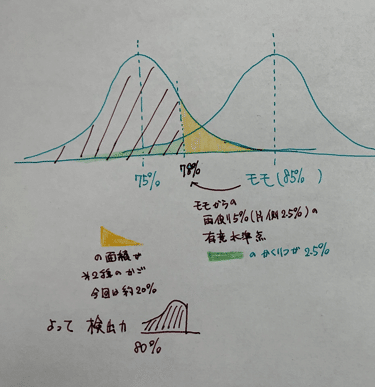
右の山がメインモモ(帰無仮説)側の正規分布、左がマスカット(対立仮説)側の分布です。
上の図だと、モモが棄却できなくなる点から右側のオレンジ色の部分が第2種の過誤が起きる確率で、残りが検出力になります。
検出力は何によって決まるのか?
この検出力は何によって決まるのでしょうか。大きく三つの要素があります。
①帰無仮説と対立仮説の平均の差
②帰無仮説の優位水準
③それぞれの標準偏差(バラツキ)の大きさ
です。 ちなみに、バラツキはサンプルサイズに大きく依存します。
$$
\sigma = \sqrt {p(1-p)/n}
$$
pが好きな確率、nがサンプルサイズです。$$これで検出力が計算できるので、その計算をもとに考えている件出力を担保するために、ここでサンプルサイズを検討する必要が出てくるのです。
適切なサンプルサイズは?
適切なサンプルサイズというのはこの件出力をどれくらいにするかを考えることである程度考えられます。
統計検定では、検出力は80%とか85%くらいを担保する際のサンプルサイズ計算が多く出てきていたような気がします。そのあたりが普通なのかもしれません。
上の計算では期せず、80%の検出力くらいになったので、検出力85%になるサンプルサイズを考えて最後にしましょう。
上のグラフを標準正規分布になるように書きなおしたのが下のグラフです。
帰無仮説側を 平均0、標準偏差1になるようにしたときに
どのようなグラフだと検出力が85%になるかと考えると
平均 -3、標準偏差が1のときに大体検出力が85%になります。
(どちらも標準偏差が1の場合、二つの平均の差が3あるとよい。このあたりが検出力85%を使う意味なのかもしれません。)
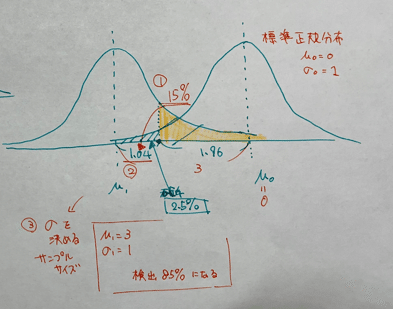
標準化を今回のケースに割り戻すと、サンプルサイズが115あると検出力は85%まで大きくなりそうです。
(長くなったので細かい計算は省略します)
このような形で、検定で大枠差がありそうだなと考えるところに加えて
プラス1 実際差があるとしたときにどれくらいの検出力がありそうか、
差があるとなった場合、(結果の平均の予測とか分散の仮定を置かなければいけないところはありますが)差がある側に80とか85%の検出力を担保するには最低これくらいサンプル必要だよね みたいなことを考える参考になればと、マスカットグミおいしいなぁと思っています。
ちなみに、さいきんのおすすめはイチゴのグミです
ここまで読んでいただきありがとうございます。 スキを押していただけると嬉しいです。 フォローしていただけるとさらにうれしいです。
