7か所あるスタンプラリーの巡り順はいくつある?(解説)
問題はこちら:
答え:13699通り
7か所の観光地を好きなように巡って、途中で辞めちゃう人のパターンも含めると全部で13699通りのスタンプの並びが出来ます。どのように数え上げるか、まず少中学生の皆さんでもわかる考え方を解説します。次に高校で習う漸化式を用いた方法でも説明します。
解説1:3か所くらいで考えてみよう
いきなり7か所で考えると大変なので、まずは3か所くらいで数え上げ方を経験してみましょう。
観光地に1,2,3と番号を付けます。こうするとスタンプの並びは123とか231とか31などと数字で表現できますね:

次にスタンプの並びを分類します。観光地を全部巡れた人は、どのような巡り順だとしてもスタンプの数は3個です。つまりスタンプの数=桁数で分類できるわけです:

3か所全部巡れた人は3桁の数字になります。一番上の桁には1,2,3のいずれかの数字が来ます。次の2桁目では1桁目で使った数字は使えないので残りの2つの数字のどちらかが入ります。最後の桁は残った数字のみになります。これを樹状に描いてみましょう:

ここから3か所全部巡れた場合のパターン数は、

このように各桁で取りうる数字の数を掛け算する事で求める事が出来ます。
次に2か所しか巡れなかった人の場合を考えてみましょう。考え方は一緒です:

2か所なので2桁の数字で表現されるわけですが、一番上の桁は3か所のいずれかになるので3通り。次の桁は残った2つの観光地のいずれかが入れるので2通りです。よって、

こういう感じの樹状図になり、パターン数は、
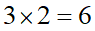
6通りになるのが分かります。
最後1か所しか巡れなかった人は、スタート地点の観光地の番号のみですから、敢えて樹状(?)で描くと、

こうなりまして、パターン数も、

とわかります。これで全パターンを網羅しました。
ここで各桁ごとのパターン数の式を改めて並べてみます:

そうなんです。巡った観光地の数が少なくなる毎に掛ける数が右側から一つずつ減っていくんですね。これがこの問題の数え上げ方の大きなポイントになります。
観光地の数が7つでも考え方はまったく一緒です。全部巡れた人は7×6×5×4×3×2×1通りの巡り方になりますし、4つしか巡れなかった人は7×6×5×4通り考えられるわけです。観光地の数ごとでパターン数を求めて全部足せば欲しい答えを得られます。一応式を挙げておきますね:

計算自体は手計算でやっても勿論良いですし、電卓叩いてもExcelで求めても何でもOKです。別に式を変形して綺麗に…とか考えないで下さい。大切なのは「解く手順を導いて計算して答えを出す事」ですからね(^-^)。綺麗とか美しくというのは後から(必要になってから)でも十分です。
解説2:漸化式で逐次的に求める
ここからは高校生の範囲です。上のなが~い式。良く見ると規則性があるのがわかります。すべての式に7が含まれていますから、7でくくる事が出来ますよね。試しにくくってみましょう:

括弧の中の最後の1以外の段に注目です。これ、観光地が6つの場合のパターン数になっています。つまり観光地の数をnとして、その巡るパターン数をSnとすると、上の式は、

こういう関係になっているんです。観光地の数が6の場合も、
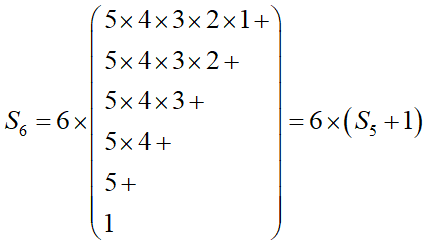
やはり一つ少ない観光地が5つのパターン数から求める事ができるのが分かります。そう、これは漸化式の関係になっているんですね。上の傾向からそれが、

である事は自明ですね。観光地が1つしか無い場合はもちろんSn=1です。後はS1からS2を、S2からS3をと計算して行けばS7=13699通りを求める事が出来ます。

もし観光地が8つだった場合は、S7から、

109600通りになる事もすぐに分かります。芋づる式に答えが導けるのが漸化式の良さですよね。
深掘り:この漸化式…解けるの?
さてここからは深堀、大学の世界に突入です。先の漸化式、解けると嬉しいですよね。その式にnをポーンと放り込むだけで答えが出ますから、S1から計算を繰り返さなくて良くなるわけです。
一般に漸化式の殆どは解けないのですが、今回の漸化式、

これはどうかというと…解けます!ただし高校の範囲の漸化式では解けません。「特殊関数」という文字通り特殊な関数が入る式になります。なので範囲としては大学の範囲なのですが、展開自体は高校生でも十分に理解できるとても興味深い物だと思いますので、是非ご覧下さい!
階乗型の漸化式
上の漸化式はSnに項数nが掛け算される形になっています。このような漸化式は階乗的になる事が知られています。そこで両辺を(n+1)!で割ってみます:

左辺と右辺でかなりいい感じの関係が出てきました。ここで、

と置くと上式は、

となります。シンプルで綺麗な形になっていますが、階乗の分数があるのが大分悲劇的です。
ここでAnを展開してみましょう:

という事でAnは1~n-1までの階乗の逆数の和なんですね。Anがわかれば、

とSnの式も求まるので、このAnをnの式で表現できれば漸化式が解けます!
順列でAnを表してみる
さて、ここでAnの分母を(n-1)!とする分数に直してみます:

ちょっと長くて済みませんがこんな感じになります。でです、ここで「順列」を思い出してみましょう。順列は次のような式でした:

このnをn-1として、またrにn-1,n-2,n-3…を入れて展開してみます:

右辺に注目です。これ、先程のAnの分子の並びとぴったり同じですよね。そうなんです、このAnは順列を用いて、

順列の足し算で表現できるんです。ここからが面白い所です。
第2種不完全ガンマ関数登場!
ここで突然ですが「第2種不完全ガンマ関数」という特殊関数を持ち出します。これはこういう形をしています:

あばばばってならないで下さい。大丈夫です。積分の中は皆さんが良く知っているtの多項式にeの-t乗が掛け算されているだけです。この定積分はxとaの2つの変数で値が決まる事に注意して下さい。
この第2種不完全ガンマ関数を頑張って解いてみます。aはどのような数でもOKなのですが、ここでは自然数とします。まず右辺を部分積分します。高校で習ったあれです。e^(-t)の方を積分して外に出します:

右辺第1項は具体的に求められますが、そのためにちょっとだけ大学の範囲の定理を使います。大学で「ロピタルの定理」というのを習います。これは分数の形をした極限を求める時に使える定理で、簡単に言えば「特定の条件を満たしていれば分母と分子を微分しても極限の結果は変わらない」という物です。上の右辺第1項でそれを見てみます:

分母分子をそれぞれtで微分していくと、分子の多項式がいずれt⁰になってtが消えます。一方分母は常にeのt乗なので、最下段の式からこの極限が0なのがわかります。ちなみに上式はロピタルの定理の条件を満たしているのでこの計算が出来ます。
これより右辺は、

こうなります。で、右辺第2項の積分ですが、これ第2種不完全ガンマ関数の形になっているのが分かりますでしょうか。Γ(x, a-1)ですよね。つまり上式は、

こういう第2種不完全ガンマ関数の漸化式になっているんです。うまいこと出来ているんですね~この関数は。
ここでx=1として上の式に代入すると、

多項式の項が消えてぐっと簡単になります。
この漸化式を展開してみます。右辺にある不完全ガンマ関数をもう一段下げてみましょう:

何か法則性が見えてきますよね。さらにもう一段下げてみます:

このように係数が規則性のある連続した掛け算の形になって展開されていきます。今aは自然数でしたから、このまま段を下げて行くといつかどこかで(a-a)という形が出てきます。つまり右辺にある第2種不完全ガンマ関数にゼロを掛ける展開がやって来るわけです。そこまで行くと、

このように完全に展開しきれます!ここで格段の係数に注目して下さい。これ…順列です!そう、ここに順列が登場するんです。そこで上式を順列で書き直してみると、

きれ~~に順列の足し算で書き直せます。さらにすべての項にeの-1乗が入っているのでそれをくくって整理すると、

こんな美しい形になるんですねぇ。
はい!ここで大分前に出てきたAnの式を再掲しますよ!

両方の式に刮目。まっったく同じΣがあります(a=nで同じ)!よって上の第2種ガンマ関数の式にあるΣをAnの式に代入すると、

こうなりまして、そしてAnがわかれば今回の問題のパターン数であるSnもわかるのでした!

分母分子の階乗がバッサリと相殺されて滅茶苦茶シンプルですっきりした式になりました!第2種不完全ガンマ関数という特殊関数を持ち出す事で、今回の漸化式は見事に解けるんです。
解けたのなら試してみましょう!今回の問題はS7ですから、上式にn=7を代入すれば答えである13699が出て来るはずです。実際に計算してみます。第2種不完全ガンマ関数は積分の形としては式を解く事ができないものなので、数値計算で近似します。以下のサイトで高精度な値を求める事が出来ます。有難い!
これによると、Γ(1,7)は、

くらいの値のようです。一方Snの式中にあるネイピア定数eは、同じく
このサイトで高精度に求めてみると、

こういう値になるようです。これらをS7の式に代入すると、

めっさ凄い精度でばっちり出ます!!
終わりに
7つの観光地を巡るパターンを数え上げる今回の問題。中学の範囲でももちろん求められますし、高校の範囲で漸化式を持ち出して求める事も出来ました。そして、その漸化式も有難い事に第2種不完全ガンマ関数を利用する事で美しくてシンプルな形に解く事が出来ました。
今回の問題、問題を考えた段階で実は漸化式になる事、そしてその漸化式が解けるかどうかすらも僕の中ではわかっていませんでした。手を動かしてみたら漸化式が出てきた。そしてこれ何か解けそうな形をしているんだけどもなぁ…と色々調べている中で階乗の逆数の和と第2種不完全ガンマ関数との関係を知り解決に至りました。数学の美しさをまた垣間見られて嬉しくなりました。
ちなみに、今回の式展開中に出てきたAnでnを∞まで飛ばした以下の式が、

である事は本当に神秘的です。これは大学で習うマクローリン展開という多項式近似を使うと証明出来ます。大学数学はこんな感じの神秘的で素敵な出会いの連続です。高校受験の数学の先にはめちゃくちゃ面白い世界が沢山待っています。今高校生の皆さんはお楽しみに。今大学生の君は人生で2度と無い貴重な学びの機会を与えられていますから、絶対にこのチャンスを逃さないように!そして大人の皆さん、大学に通わなくても今は教えてくれる数学系のサイトや動画が沢山ありますので、是非その門を叩いて開いてみて下さい!
ではまた(^-^)/
この記事が気に入ったらサポートをしてみませんか?
