
社会人のための学び直し数学【高校数学2次関数編その5】
5.2次不等式
今回は,2 次関数のグラフを利用する 2 次不等式の解法を考えていきます。
最初に,これまでは詳しい説明なしですませてきた,$${x-2<0}$$ のような不等式について見てみましょう。
$${x-2<0}$$ は $${x-2}$$ が $${x}$$ の 1 次式なので 1 次不等式といいます。そして,$${x-2<0}$$ を満たすような $${x}$$ の集合を求めることを,不等式を解くといいます。1 次不等式 $${x-2<0}$$ は,$${x}$$ から $${2}$$ を引くと負の数になるのだから,$${x}$$ は $${2}$$ より小さいはずで,それは $${x<2}$$ と書けます。すなわち 1 次不等式 $${x-2<0}$$ の解は $${x<2}$$ となります。
1 次方程式と同様に 1 次不等式の解法にも形式的な手法があります。
まず,次の性質を納得してください。
$$
A>B⇔A+C>B+C
$$
すなわち,大小関係がはっきりしている $${A,B}$$ に同じ数 $${C}$$ を加えても,相互の大小関係に変化はないということです。
【注】この性質において $${A,B,C}$$ は必ず実数です。$${A,B,C}$$ が虚数である場合,それらに大小関係は存在しません。
すると $${x-2<0}$$ より $${x-2+2<0+2}$$ から $${x<2}$$ となります。
そして,1 次方程式で $${A=B⇔A+C=B+C}$$ の関係から,移項という計算手法が導けたように,不等式についても移項という手法が導けるのです。それは以下のような考え方です。
$${x-2+2<0+2}$$ の $${-2+2=0}$$ は書かないこととして $${x<0+2}$$ とすれば,$${x-2<0}$$ で不等号の左(左辺)の $${-2}$$ を不等号の右(右辺)へ移動して,その際,符号を変化させる。
すなわち,$${x-2<0}$$ において $${x<0+2}$$ とできると考えるのです。この手法を 1 次方程式の場合と同様に移項という訳です。
$${x-3<0}$$ をこの手法で解いてみましょう。
左辺の $${-3}$$ を右辺に移項します。$${x<0+3}$$ となって,$${x<3}$$ が解です。
次に,不等式 $${(x-2)(x-3)>0}$$ の解法を考えます。
$${(x-2)(x-3)=x^2-5x+6}$$ と展開できて 2 次式なので,
$${(x-2)(x-3)>0}$$ は 2 次不等式です。
そして 2 つの数 $${x-2}$$ と $${x-3}$$ の積が正となるような $${x}$$ の値の範囲を求めれば,2 次不等式を解いたことになります。
さて,2 数の積が正となるとき,それぞれは同符号でなければなりません。ということは,
$${x-2<0}$$ かつ $${x-3<0}$$
または
$${x-2>0}$$ かつ $${x-3>0}$$
でなければなりません。
【注】「かつ」は「ともに成り立つ」であり,「または」は「少なくとも一方が成り立つ」という用語です。「少なくとも一方が成り立つ」には,「ともに成り立つ」場合があるなら,それも含みます。
$${x-2<0}$$ かつ $${x-3<0}$$ は,
$${x<2}$$ かつ $${x<3}$$ ですから,
結局 $${x<2}$$ です。
$${x-2>0}$$ かつ $${x-3>0}$$ は,
$${x>2}$$ かつ $${x>3}$$ ですから,
結局$${x>3}$$($${3<x}$$ とも書く)です。
したがって,$${(x-2)(x-3)>0}$$ の解は
$${x<2}$$ または $${3<x}$$($${x<2,3<x}$$ とも書く)となります。
図で確認すると,

であり,確かに $${x<2,3<x}$$ です。
それでは本題,2 次関数のグラフを利用する解法です。この解法は,上述の解法より直感的に理解できます。
少し準備をしましょう。
$${xy}$$ 平面上で,$${x}$$ 軸(横軸)より上の方は $${y>0}$$ であり,$${x}$$ 軸より下の方は $${y<0}$$ となります。それぞれ,$${y>0}$$ の表す領域(または,領域 $${y>0}$$),$${y<0}$$ の表す領域(または,領域 $${y<0}$$)といいます。詳しく説明すると,領域 $${y>0}$$ 上の点 $${(x,y)}$$ であれば,すべての点について $${y>0}$$ となり,領域 $${y<0}$$ 上の点であれば,すべての点について $${y<0}$$ となるということです。
次に,放物線 $${y=x^2-5x+6}$$ と $${x}$$ 軸との交点を求めます。前回4でやったように,2 次方程式 $${x^2-5x+6=0}$$ の解が交点の $${x}$$ 座標を与えます。$${(x-2)(x-3)=0}$$ から $${x=2,3}$$ となるので,
求める交点は $${(2,0),(3,0)}$$ です。
準備は整いました。
$${y=x^2-5x+6}$$ のグラフを,特に $${x}$$ 軸との交点を意識して描きます。
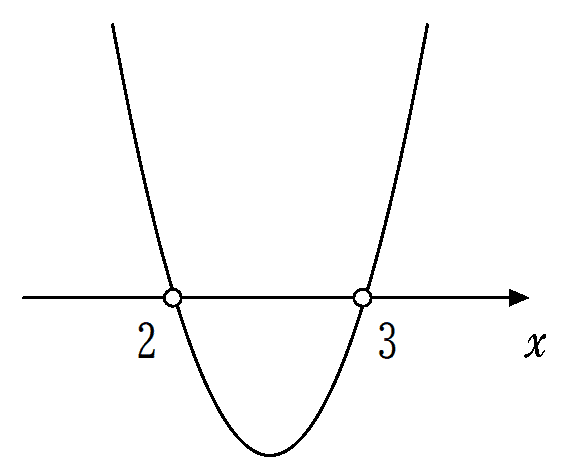
そして,$${(x-2)(x-3)>0}$$ となるのは
$$
y=x^2-5x+6=(x-2)(x-3)>0
$$
より,$${y>0}$$ となるところだから,グラフが $${x}$$ 軸より上,すなわち,領域 $${y>0}$$ の部分に存在するような $${x}$$ の値の範囲を考えます。したがって,$${x<2,3<x}$$ です。

図5-2を参考に,2 次関数のグラフの利用法を確認してください。
練習問題 2 次不等式 $${(x-2)(x-3)<0}$$ を解け。
[ヒント]$${y=x^2-5x+6}$$ のグラフが,領域 $${y<0}$$ にある $${x}$$ の値の範囲を求めます。
【答】$${2<x<3}$$
この記事が気に入ったらサポートをしてみませんか?
