
#39 まりなのiPhoneの容量 ムーアの法則に従ってる説
どうも、まりなです。
最近携帯を買い換えました。iPhone14 proです。

どんどん高くなる機種代に恐れ慄くことしかできませんがAppleへのお布施だと思ってproにしました。容量は128GBにしました。前の11 proは64GBだったのですが音楽や写真で容量が限界を迎えていたのも機種変更した理由の一つです。
容量の話をしているといつもコンピュータアーキテクチャの講義で習った「ムーアの法則」が思い浮かびます。
The complexity for minimum component costs has increased at a rate of roughly a factor of two per year.
情報工学に詳しくない人向けに要約すると「容量は1年ごとに倍になる」ということを言っています。のちに予想を修正し「2年ごとに倍になる」とされました。
法則と言っても原理を証明されたものではなくただの経験則なのですが実際ムーアの法則は半導体集積率を高精度に予測しています。

小学生の頃DSiに指していたのは1GBのSDカードでしたが今Switchにさしているのは128GBのmicroSDです。それでいて値段も同じくらいなのだから半導体技術の進歩の早さは身をもって感じられるほど凄いものです。
ところで半導体がなぜデータを記録できるのか疑問に思ったことはありませんか?あんな電気を微妙に通すだけのものが音楽や写真を記録していると思うと不思議じゃないですか?不思議じゃない人は「ようやく本題」まで読み飛ばしていただいて大丈夫です。不思議な人にはちょっと長くなりますがスマホやPCのストレージ(SSD)の仕組みをちょっと解説してみようと思います。
まず中学理科の復習からすると、「電気を通す」とは何かというと電子が動けるということです。電気を通すものの代表である金属は自由電子というよく動く電子を持つため電気が通ります。では半導体はというと、よく動く電子を「微妙に持っている」、あるいは「電子が微妙に足りない」物質です。電子が足りない物質も電気を通すの?と疑問に思うかもしれませんが供給された電子を受け取りやすい物質と考えれば良いと思います。

電子を微妙に持っている方の半導体をn型半導体といい、電子が足りない方の半導体をp型半導体といいます。これらを組み合わせて次のようなものを作ります。

これの何が凄いかというと電気で制御できるスイッチのような振る舞いをするのです。どういうことかというと普段は上図のBとCの端子は繋がっていないため電気は通りません。しかし上図のAの端子に電圧(+)をかけると電子が端子の下に引き寄せられます。するとBとCの端子がつながり電気が通るようになります。

AがオフならB-Cに電気は流れない、AがオンならB-Cに電気が流れるスイッチが半導体で作れました。これを組み合わせて次のような回路を作ります。
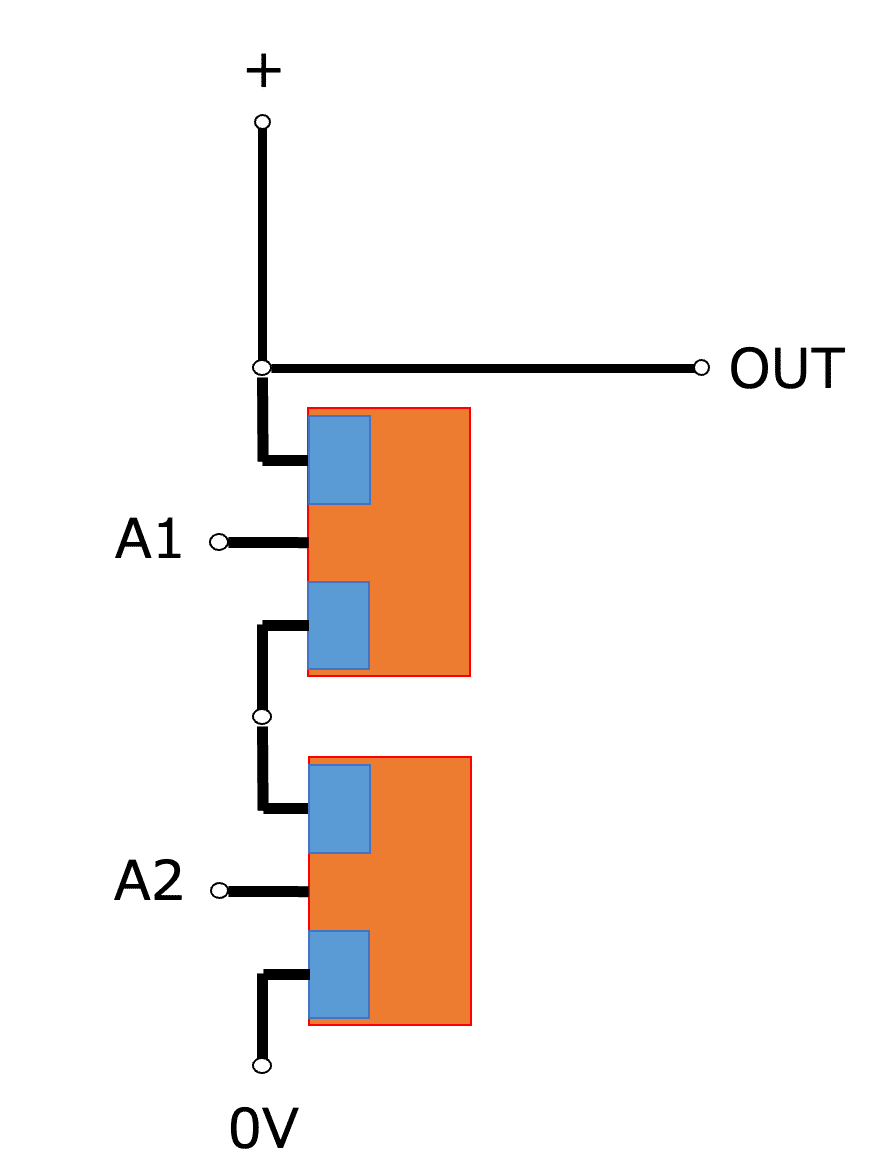
この回路の動作を考えるとA1とA2が共にオンの時だけOUT端子は0VにつながりOFFとなり、それ以外の時はONとなります。

これをNANDゲートといい、次のように省略して表記します。

ずっと何の話をしているんだデータの記録はどうしたんだと思われるかもしれませんが実はもうストレージの完成まであと一歩というところまで来ています。
今更ながらストレージが満たすべき機能とは具体的に何でしょうか?音楽も画像も文章も保存したり読み出したりできて…と考えると複雑そうですが音楽も画像も文章も2進数の数列として表記できます。音楽なら各時刻の振動値を、画像なら各画素に対応する赤、緑、青の画素値を、文章なら各文字の文字コードを2進数で表せばデータは2進数の数列として表現できます。
ここまで使ってきたOFF (0V)とON (+)という表現はそれぞれ0と1に割り当てられます。
どんなデータも0と1の列として表現できるならストレージが果たすべき機能は次のたった二つで済みます。
保存されたデータを記憶しておく(保持モード)
入力したデータを保存する(書き込みモード)
NANDゲートを組み合わせて次のような回路を作ります。

これでストレージの完成です。この回路が上の1.と2.の機能を果たしているか確認してみます。
まず「保持モード」の時、"モード"を0とします。NANDゲートは両方の入力がON(1)の時しかOFF(0)を出力しないため②の出力は"1"となります。
よって④の入力は上が"メモリ"、下が"1"となります。

ここでNANDゲートの入出力関係を振り返ってみるとA2が"1”の時、OUTはA1の逆になっています。

よって④の出力は"メモリの逆"になります。メモリが"0"なら"1"、メモリが"1"なら"0"を出力します。よって③の入力は上が"1"、下が"メモリの逆"です。

またNANDゲートの入出力関係を振り返るとA1が"1"の時はOUTはA2の逆になっているので③の出力は"メモリの逆の逆"、すなわち"メモリ"そのものということになります。

これは"0"が保存されていたら"0"を、"1"が保存されていたら"1"をメモリに出力するということになります。つまり結局保存されていたデータを巡り巡ってそのまま返しています。これがデータを「保持」するということです。
「書き込みモード」も確認してみます。モードには"1"を入力します。
①の入力は"入力"と"1" となるので"入力の逆"を出力します。
②の入力は"入力の逆"と"1"なので出力は"入力の逆の逆" = "入力"になります。
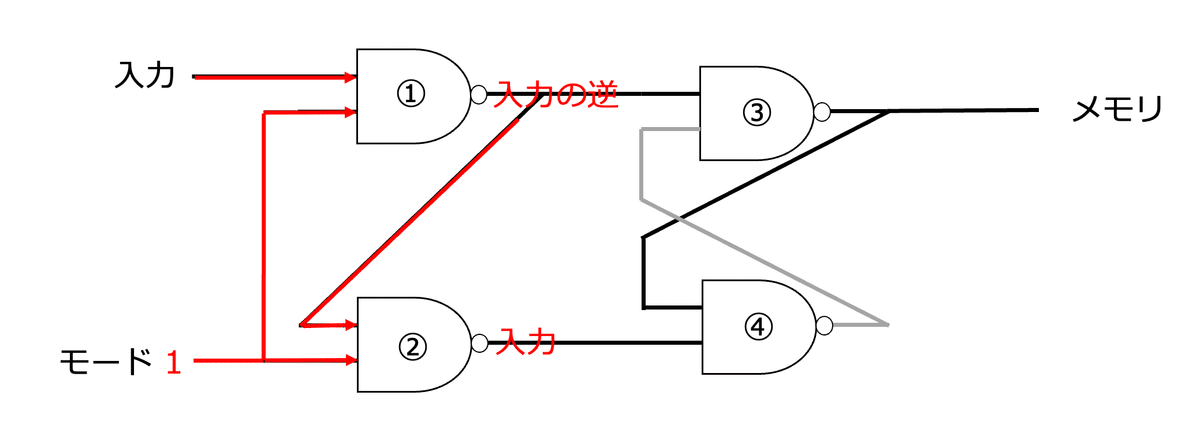
ここからはややこしいので入力を場合分けして考えます。
"入力"が"0"の場合、④の下の入力は0となるので、"1"を出力します。よって③の上の入力は"入力の逆" 、下の入力は"1"となるので、出力は"入力の逆の逆" = "入力"となり、メモリは"入力"になります。

"入力"が"1"の場合、③の上の入力は"0"となるので出力は"1"となり、メモリは"1" = "入力"になります。

よって入力が"0"でも"1"でもメモリは入力に一致します。入力したデータをメモリに保存することが確かめられました。
この回路で保存できるのは1ビット(=1桁の二進数)のみです。これを大量に並列することで何GBものデータを扱うストレージはできています。
ようやく本題
やっと本題に戻れます。では私のiPhoneの容量はムーアの法則に従っているのでしょうか!?結果をグラフにしてみました。

青色がムーアの法則による予想値でオレンジ色が私のiPhoneの容量の推移です。縦軸は基数2の対数軸になっているのでムーアの法則は傾き1の直線になっています。全体的にムーアの法則の予想値を下回っていることがわかりました…
まとめ
ということでせっかく買い替えたところなのになんか損してる気分になってしまいました。まあムーアの法則はすでに限界を迎えているとも言われてますしね。そんなにスマホの容量あっても持て余しますしね。みなさんもムーアとバトルしてみてはいかがでしょうか、それでは。
この記事が気に入ったらサポートをしてみませんか?
